ОГЭ математика 2022. Разбор варианта Алекса Ларина № 294.
Больше разборов на моем ютуб-канале
Задания 1-5
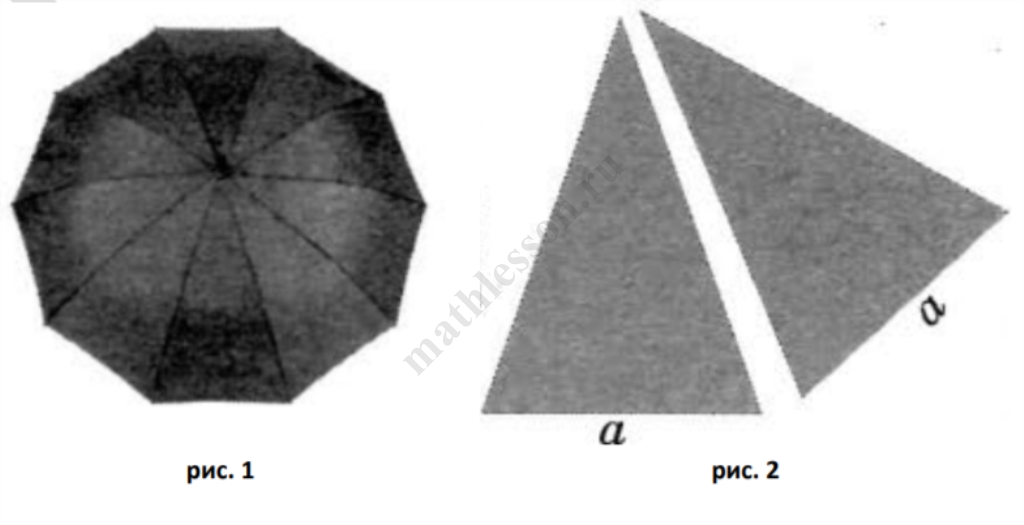
Два друга, Коля и Боря, задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из десяти отдельных клиньев, натянутых на каркас из десяти спиц (см. выше рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Коля и Боря сумели измерить расстояние между концами соседних спиц a(см. выше рис. 2). Оно оказалось равно 36 см. Высота купола зонта h(см. выше рис. 3) оказалась равна 20 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – 116 см.
1. Длина зонта в сложенном виде равна 27 см. Она складывается из длины ручки (см. выше рис. 4) и трети длины спицы (зонт в три сложения). Найдите длину спицы (в см), если длина ручки зонта равна 6,5 см.
2. Поскольку зонт сшит из треугольников, рассуждал Коля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности (в см 2) зонта методом Коли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 58,8 см. Ответ округлите до десятков.
3. Боря предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола (в см), зная, что OC=R (см. выше рис. 3).
4. Боря нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S=2\pi Rh$$ , где R – радиус сферы, а – высота сегмента. Рассчитайте площадь поверхности купола зонта (в см2) методом Бори. Число $$\pi$$ округлите до 3,14. Ответ округлите до целого числа.
5. Рулон ткани имеет длину 25 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 16 зонтов, таких же, как зонт, который был у Коли и Бори. Каждый треугольник, с учётом пропуска на швы, имеет площадь 1 110 см2. Оставшаяся ткань пошла на обрезки. Сколько процентов ткани рулона пошло на обрезки?
Задание 7
Числа x и y отмечены точками на координатной прямой. Расположите в порядке возрастания числа $$\frac{1}{x}$$, $$\frac{1}{y}$$ и 1. В ответе укажите номер правильного варианта ответа.
- $$\frac{1}{x}, 1, \frac{1}{y}$$
- $$\frac{1}{y}, 1, \frac{1}{x}$$
- $$\frac{1}{x}, \frac{1}{y}, 1$$
- $$1, \frac{1}{y},\frac{1}{x}$$
Задание 11
На рисунке изображены графики трёх функций. Установите соответствие между графиками функций и формулами, которые их задают. В ответе укажите последовательность цифр, соответствующих А, Б, В, без пробелов, запятых и других разделительных символов.

- $$y=x^{2}+4$$
- $$y=-2x+4$$
- $$y=\sqrt{x}$$
- $$y=\frac{4}{x}$$
Задание 12
Полную механическую энергию тела (в джоулях) можно вычислить по формуле $$E=\frac{mv^{2}}{2}+mgh$$, где m — масса тела (в килограммах), v — его скорость (в м/с), h — высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а g — ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите m (в килограммах), если E = 336 Дж, v = 6 м/с, h = 3 м, а g =10 м/с2.
Задание 14
Ире надо подписать 880 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Ира подписала 10 открыток. Определите, сколько открыток было подписано за восьмой день, если вся работа была выполнена за 16 дней.
Задание 19
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.
- Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
- В тупоугольном треугольнике все углы тупые.
- Средняя линия трапеции равна полусумме её оснований.