ОГЭ математика 2018. Разбор варианта Алекса Ларина № 185.
Решаем ОГЭ 185 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №185 (alexlarin.com)
Решаем ОГЭ 185 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №185 (alexlarin.com)
Задание 1
Найдите значение выражения $$\frac{1,8}{1+\frac{1}{11}}$$
$$\frac{1,8}{1+\frac{1}{11}}=$$$$\frac{18}{10}*\frac{11}{12}=$$$$\frac{33}{20}=1,65$$
Задание 2
| Команда | 1 эстафета, мин. | 2 эстафета, мин. | 3 эстафета, мин | 4 эстафета, мин |
| Ласточка | 3,4 | 4,9 | 2,9 | 5,8 |
| Чайка | 4,5 | 4,3 | 3,2 | 5,4 |
| Буревестник | 4,9 | 4,8 | 2,7 | 6,3 |
| Альбатрос | 3,7 | 4,5 | 2,4 | 5,1 |
| Команда | 1 эстафета, место | 2 эстафета, место | 3 эстафета, место | 4 эстафета, место | итоговый бал |
| Ласточка | 1 | 4 | 3 | 3 | 11 |
| Чайка | 3 | 1 | 4 | 2 | 10 |
| Буревестник | 4 | 3 | 2 | 4 | 13 |
| Альбатрос | 2 | 2 | 1 | 1 | 6 |
В итоге команда Буревестник займет 4 место, что соответствует 4 варианту ответа
Задание 3
Между какими числами заключено число $$2\sqrt{3}$$ Варианты ответа 1)12 и 13 2)3 и 4 3)5 и 6 4)6 и 7
$$2\sqrt{3}=\sqrt{2^{2}*3}=\sqrt{12}\Leftrightarrow$$$$\sqrt{9}<\sqrt{12}<\sqrt{16}$$, что соответствует $$3<2\sqrt{3}<4$$ и является 2 вариантом ответа
Задание 4
Представьте выражение $$\frac{(c^{-9})^{2}}{c^{-4}}$$ в виде степени с основанием с Варианты ответа: 1) $$c^{-22}$$ 2) $$c^{-72}$$ 3) $$c^{68}$$ 4) $$c^{-14}$$
Воспользуемся свойствами степени: $$\frac{(c^{-9})^{2}}{c^{-4}}=$$$$\frac{c^{-18}}{c^{-4}}=c^{-18-(-4)}=$$$$c^{-14}$$, что соответствует 4 варианту ответа
Задание 5
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры с 6:00 до 18:00. Ответ дайте в градусах Цельсия.
min=12 (6:00) , max=24 (12:00-15:00), тогда max-min=24-12=12
Задание 6
Решите уравнение $$3(2-3x)-(2x+1)=27$$
$$3(2-3x)-(2x+1)=27\Leftrightarrow$$$$6-9x-2x-12-27=0\Leftrightarrow$$$$-11x=22|:-11\Leftrightarrow$$$$x=-2$$
Задание 7
Рабочий выточил за смену 920 деталей, превысив план на 15%. Сколько деталей предполагало выточить?
Пусть первоначально планировалось выточить х деталей, тогда мы можем принять эту величину за 100%: x-100% 920-115% Тогда: $$x=\frac{920*100}{115}=800$$ деталей
Задание 8
На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 8 млн пользователей.
1. пользователей из России больше, чем пользователей из Украины - верно 2. больше трети пользователей сети — из Украины - неверно (так как сегмент Украины менее трети всей окружности) 3. пользователей из Беларуси больше, чем пользователей из Украины - неверно (так как сегмент Беларуси меньше сегмента Украины) 4. пользователей из России больше 4 миллионов человек - верно. Ответом будут 2 и 3 варианты
Задание 9
В корзинке у Красной Шапочки 20 пирожков, 4 из которых с мясом, 7 с картошкой, а остальные с капустой. Бабушка наугад взяла один пирожок. Какова вероятность того, что бабушка взяла пирожок с капустой?
Количество пирожков с капустой: 20-4-7=9. Тогда вероятность взять пирожок с капустой составляет: $$P=\frac{9}{20}=0,45$$
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают
1) $$y=2x$$ - линейная функция, графиком является прямая, что соответствует пункту Б 2) $$y=x^{2}-2$$ - квадратичная функция, графиком является парабола, что соответствует пункту А 3) $$y=-\frac{2}{x}$$ - обратная пропорциональность, графиком является гипербола, что соответствует пункту В В итоге ответ будет 213
Задание 11
Укажите номер первого отрицательного члена арифметической прогрессии: 9,5; 9; 8,5; …
Найдем разность арифметической прогрессии: $$d=a_{n+1}-a_{n}=9-9,5=-0,5$$, $$a_{1}=9,5$$. По формуле N-ый член арифметической прогрессии вычисляется как: $$a_{n}=a_{1}+d(n-1)$$. Тогда $$9,5-0,5(n-1)<0 \Leftrightarrow$$$$9,5-0,5n+0,5<0\Leftrightarrow$$$$10<0,5n|:0,5\Leftrightarrow$$$$n>20$$. Так как неравенство строгое, и n - порядковый номер, то первый отрицательный член будет под номером 21
Задание 12
Найдите значение выражения $$(\frac{2}{a}+\frac{1}{b})\cdot \frac{1}{a^{2}+4b^{2}+4ab} \cdot (a^{2}-4b^{2})$$
$$(\frac{2}{a}+\frac{1}{b})\cdot \frac{1}{a^{2}+4b^{2}+4ab} \cdot (a^{2}-4b^{2})=$$$$\frac{2b+a}{ab}\cdot \frac{1}{(a+2b)^{2}} \cdot ((a-2b)(a+2b)=$$$$\frac{a-2b}{ab}=$$$$\frac{2\sqrt{5}+2-2(\sqrt{2}-1)}{(2\sqrt{5}+2)(\sqrt{5}-1)}=$$$$\frac{2\sqrt{5}+2-2\sqrt{5}+2}{2(\sqrt{5}+1)(\sqrt{5}-1)}=$$$$\frac{4}{2(5-1)}=\frac{1}{2}=0,5$$
Задание 13
Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта позволяет формула $$F=1,8C+32$$ , где С — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует $$186^{\circ}$$ по шкале Фаренгейта? Ответ округлите до десятых.
Подставим в формулу известные значения: $$186=1,8C+32\Leftrightarrow$$$$1,8C=154|:1,8\Leftrightarrow$$$$C=85,(5)$$. Так как дробь бесконечная десятичная, то если округлить до десятых получим: $$85,555...=85,6$$
Задание 14
Задание 15
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
Опустим перпендикуляр из точки C как показано на рисунке. BC=DE=8, BD-CE=3, тогда из треугольника ABC: $$AB=\sqrt{AC^{2}-BC^{2}}=\sqrt{10^{2}-8^{2}}=6$$. Тогда AD=6+3=9 метров
Задание 16
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 48° и 74°. Найдите меньший угол параллелограмма. Ответ дайте в градусах
Весь угол в таком случае составляет: 48+74=122. Тогда меньший острый по свойству углов параллелограмма составляет: 180-122=58.
Задание 17
В треугольнике ABC известно, что AC=24, BC= $$\sqrt{265}$$ , угол C равен 90°. Найдите радиус описанной окружности этого треугольника.
По теореме Пифагора: $$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{576+265}=29$$. По свойству радиуса описанной окружности около прямоугольного треугольника : $$R=\frac{AB}{2}=14,5$$
Задание 18
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Пусть a,b - стороны прямоугольника и параллелограмма. Площадь прямоугольника: $$S_{1}=ab$$, площадь параллелограмма: $$S_{2}=ab\sin\alpha$$, где $$\alpha$$ - острый угол между сторонами параллелограмма, тогда: $$\frac{1}{2}ab=ab\sin\alpha\Leftrightarrow$$$$\sin\alpha=\frac{1}{2}\Leftrightarrow$$$$\alpha=30^{\circ}$$
Задание 19
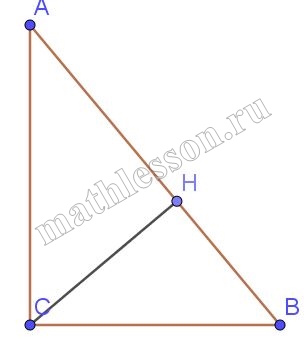
В треугольнике ABC угол C равен 90°, СН – высота, AВ = 16, sin A = 3/4 . Найдите BН.
Из треугольника ABC: $$CB=AB\sin A=16*\frac{3}{4}=12$$.
Из треугольника CHB: $$HB=CB\sin BCH$$. Но из подобия прямоугольных треугольников при проведении высоты из прямого угла получаем, что $$\sin BCH=\sin A$$, тогда $$HB=CB\sin A=12*\frac{3}{4}=9$$
Задание 20
1. Диагонали любого прямоугольника равны - верно 2. Существует прямоугольник, который не является параллелограммом - неверно, так как прямоугольник сам по себе и есть параллелограмм, у которого все углы прямые 3. Площадь треугольника меньше произведения двух его сторон - верно, так как равна половине произведения его сторон на синус угла между ними Правильными являются ответы под номерами 1 и 3
Задание 21
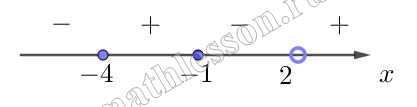
Найдите сумму целых отрицательных решений неравенства $$\frac{x^{2}+2x+10}{x-2} \geq -3$$
$$\frac{x^{2}+2x+10}{x-2} \geq -3\Leftrightarrow$$$$\frac{x^{2}+2x+10}{x-2}+3 \geq 0\Leftrightarrow$$$$\frac{x^{2}+2x+10}{x-2}+\frac{3(x-2)}{x-2} \geq 0\Leftrightarrow$$$$\frac{x^{2}+2x+10+3x-6}{x-2} \geq 0\Leftrightarrow$$$$\frac{x^{2}+5x+4}{x-2} \geq 0$$
Найдем при каких значениях x числитель дроби равен нулю и отметим эти значения (закрашенные, так как неравенство нестрогое), а так же значение, когда знаменатель равен нулю (пустое, так как мы должны исключить данное значение из ОДЗ) на координатной прямой и расставим знаки значений, которые принимает дробь на полученных промежутках:
Нам необходимо выбрать те промежутки, где дробь принимает положительные значения, а так же из данных промежутков найти сумму всех целых отрицательных значений: $$-4+(-3)+(-2)+(-1)=-10$$
Задание 22
В сплаве олова с медью содержалось 11 кг меди. После того, как в сплав добавили 7,5 кг олова, содержание олова повысилось на 33%. Какова была первоначальная масса сплава?
Пусть x кг - масса сплава, тогда x - 11 кг - масса олова в нем, а доля олова : $$\frac{x-11}{x}*100$$%. Добавили 7,5 кг олова, тогда масса олова стала : x - 11 + 7,5 = x - 3,5 кг , масса сплава при этом стала: x + 7,5 кг, следовательно, доля олова : $$\frac{x-3,5}{x+7,5}*100$$%. Тогда:
$$\frac{x-3,5}{x+7,5}*100-\frac{x-11}{x}*100=33|*x(x+7,5)\Leftrightarrow$$$$100x(x-3,5)-100(x-11)(x+7,5)=33x(x+7,5)\Leftrightarrow$$$$100x^{2}-350x-100x^{2}+350x+8250=33x^{2}+247,5x\Leftrightarrow$$$$33x^{2}+247,5x-82550=0|:16,5\Leftrightarrow$$$$2x^{2}+15x-500=0$$
$$D=225+4000=65^{2}\Leftrightarrow$$$$x_{1}=\frac{-15+65}{4}=12,5 ; x_{2}<0$$. Следовательно, первоначальная масса сплава составляла 12,5 кг.
Задание 23
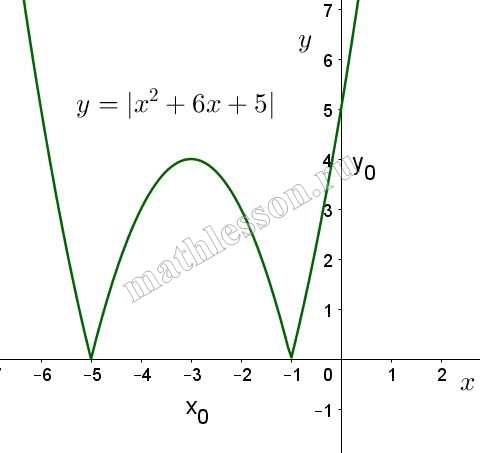
Постройте график функции $$y=|x^{2}+6x+5|$$ и определите, при каких значениях а прямая $$y=a$$ имеет с графиком три общие точки.
Рассмотрим график функции $$y_{1}=x^{2}+6x+5$$. Искомый будет отличаться от данного тем, что та часть параболы, которая находится под осью Ох симметрично отобразиться относительно оси Ох (в силу того, что модуль все отрицательные значения сделает положительными). Найдем вершину параболы: $$x_{0}=-\frac{b}{2a}=-\frac{6}{2}=-3$$ , $$y_{1}(3)=(-3)^{2}+6*(-3)+5=-4$$. Найдем еще несколько значений для функции $$y_{1}$$: $$y_{1}(-2)=-3 ; y_{1}(-1)=0 ; y_{1}(0)=5$$.
График квадратичной функции симметричен относительно оси $$x=x_{0}$$, в нашем случае относительно $$x=-3$$. Начертим график функции $$y_{1}$$:
Отобразим симметрично относительно оси Ох ту часть параболы, которая располагается под осью Ох и получим график функции $$y=|x^{2}+6x+5|$$:
Очевидно, что прямая параллельная оси Оу будет иметь три точки пересечения с графиком данной функции при $$a=4$$:
Задание 24
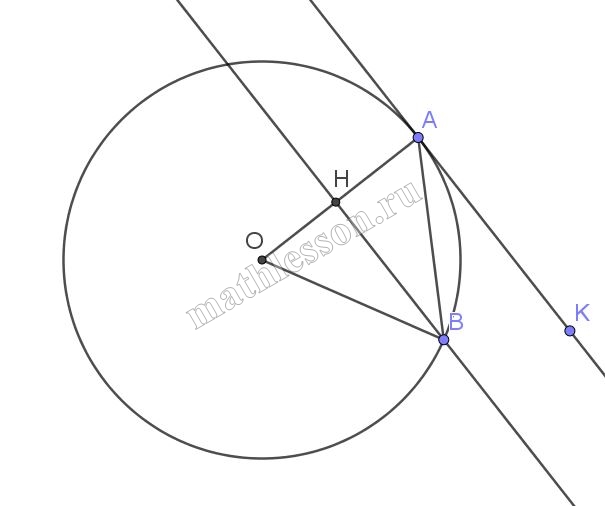
В окружности радиуса 16 см проведена хорда длиной, равной 8 см. через один конец хорды проведена касательная, а через другой – секущая, параллельная касательной. Найдите расстояние между касательной и секущей.
Задание 25
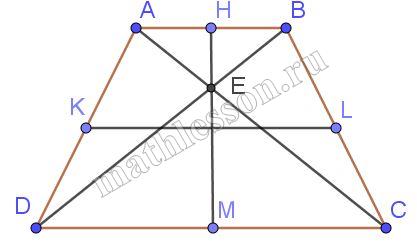
Докажите, что если в равнобедренной трапеции диагонали взаимно перпендикулярны, то высота трапеции равна средней линии.
Задание 26
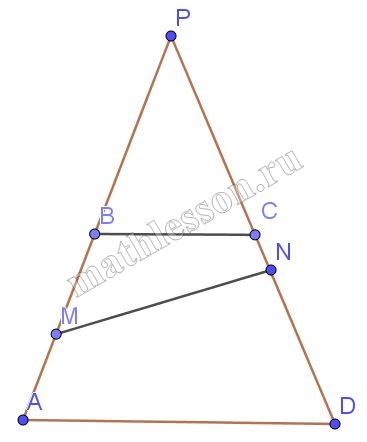
На боковой стороне АВ трапеции АВСD взята точка М таким образом, что АМ : МВ = 2 : 3. На противоположной стороне СD взята такая точка N, что отрезок MN делит трапецию на части, одна из которых по площади втрое больше другой. Найдите отношение CN : ND, если известно, что BC : AD = 1 : 2