ОГЭ математика 2023. Разбор варианта Алекса Ларина № 334.
Больше разборов на моем ютуб-канале
Задания 1-5
| Печь | Тип | Объём помещения (м3) | Масса (кг) | Стоимость (тыс. руб.) |
|---|---|---|---|---|
| Килиманджаро | дровяная | 4-8 | 45 | 14 |
| Кентавр | дровяная | 7-13 | 65 | 25 |
| Ока | электрическая | 8-14 | 14 | 23 |
$$V = 2,5\cdot2,3\cdot2,1=12,075$$ м3
$$V = 2,5\cdot2,3\cdot2,1=12,075$$ м3
Килиманджаро (дровяная) - не подходит по объёму, отапливает до 12,075 м3
Кентавр (дровяная) - 25000 руб цена
Ока (электрическая) - 6500 установка + 23000 руб цена = 29500 руб
Дровяная печь дешевле электрической на $$29500-25000=4500$$ руб
$$V = 2,5\cdot2,3\cdot2,1=12,075$$ м3
Килиманджаро (дровяная) - не подходит по объёму, отапливает до 12,075 м3
Кентавр (дровяная) - $$2\cdot1700=3400$$ руб
Ока (электрическая) - $$3000\cdot5=15000$$ руб
Дешевле эксплуатация дровяной печи Кентавр на $$15000-3400=11600$$ руб
Кентавр (дровяная)
Цена 25000>20000, по условиям магазина:
Скидка на доставку товара $$35\% \Rightarrow$$ оплачиваем $$100\%-35\%=65\%$$
$$500\cdot0,65=325$$ руб
Скидка на товар $$3\% \Rightarrow$$ оплачиваем $$100\%-3\%=97\%$$
$$25000\cdot0,97=24250$$ руб
Стоимость дровяной печи = $$325+24250=24575$$ руб
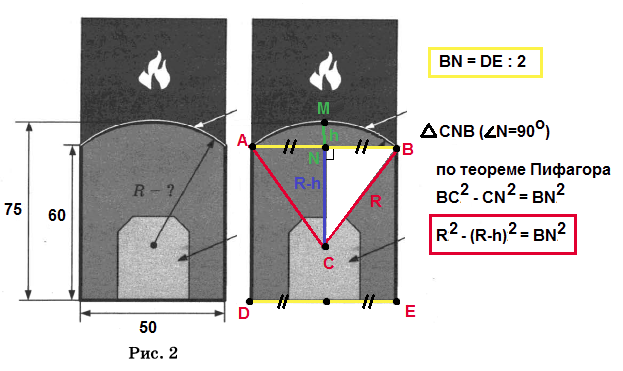
$$h = 75 - 60 = 15$$
$$BN = \frac{50}{2} = 25$$
$$R² - (R - 15)² = 25² R² - (R² - 2\cdot R\cdot15 + 15²) = 25²$$
$$R² - (R² - 30R + 225) = 625$$
$$R² - R² + 30R - 225 = 625$$
$$30R - 225 = 625$$
$$30R = 625 + 225$$
$$30R = 850$$
$$R = \frac{850}{30}=28,3$$
Задание 6
$$0,03\cdot0,3\cdot30000=0,009\cdot30000=270$$
Задание 7
Заметим, что $$-1<a<0, 0<b<1,$$ откуда $$a^3<0, a-b<0, ab<0, -1<a+b<1.$$ Таким образом, верным является утверждение $$ab<1.$$
Задание 8
$$\frac{2^{n+2}\cdot21^{n+3}}{6^{n+1}\cdot7^{n+2}}=\frac{2^n\cdot21^n\cdot2^2\cdot21^3}{6^n\cdot6^1\cdot7^n\cdot7^2}=\frac{42^n\cdot2^2\cdot3^3\cdot7^3}{42^n\cdot2\cdot3\cdot7^2}=2\cdot3^2\cdot7=14\cdot9=126$$
Задание 10
$$P(A)=\frac{1300}{100000}=0,013$$
Задание 11
А)
$$f(x)=0\Rightarrow\left[\begin{matrix} x^2-2=0\\ 53x-75=0 \end{matrix}\right.\Leftrightarrow x=\pm\sqrt{2}$$ и $$x=\frac{75}{53}$$
Очевидно, что это 2.
Б)
$$x^8-x^5+x^2-x+1=x^2(x^6+1)-x(x^6+1)+1=(x^6+1)(x^2-x)+1$$
При этом $$min(x^2-x)=(\frac{1}{2})^2-\frac{1}{2}=-\frac{1}{4}$$ и $$x^2-x=0$$ при $$x=0$$ и $$x=1.$$ При $$x\in(0;1)$$ имеем $$x^6+1\in(1;2)\Rightarrow (x^6+1)(x^2-x)$$ не выйдет за границы $$(2\cdot(-\frac{1}{4});1\cdot(-\frac{1}{4})),$$ т.е. $$(-\frac{1}{2};-\frac{1}{4})\Rightarrow$$ с учётом, что прибавляется 1, то выражение всегда положительное $$\Rightarrow 1$$ ответ.
Г)
Пусть $$x^2+x=y: \frac{1}{y}-\frac{1}{2y+3}<0\Rightarrow \frac{2y+3-y}{y(2y+3)}<0\Rightarrow \frac{y+3}{y(2y+3)}<0\Rightarrow$$
$$\Rightarrow y\in(-\infty;-3);(-\frac{3}{2};0).$$ Получим:
$$\left[\begin{matrix} x^2+x<-3\\ \left\{\begin{matrix} x^2+x>-\frac{3}{2}\\ x^2+x<0 \end{matrix}\right.\\ \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} \varnothing\\ \left\{\begin{matrix} x\in R\\ x^2+x<0 \end{matrix}\right.\\ \end{matrix}\right.\Leftrightarrow x^2+x<0\Rightarrow x\in(-1;0)\Rightarrow 4$$ вариант.
Примечание от наборщика.
Ларин - чудак, такое детям в простом варианте не дают. Маразм крепчал.
Задание 13
Можно поделить на первую скобку, так как больше нуля и знак неравенства не меняется:
$$3-2x>0$$
$$-2x>-3$$
$$2x>3$$
$$x<1,5\Rightarrow 4$$
Задание 14
Логично предположить, что в кладке с бревнами 12 рядов.
Пусть а1 = 1 - количество бревен в 1-ом ряду;
а12 = 12 - количество бревен в 12-ом ряду;
Знаменатель прогрессии d равен 1, т.к. количество бревен увеличивается на 1, если смотреть на ряды сверху вниз.
Нужна формула суммы первых n членов арифметической прогрессии.
$$S_n=\frac{(a_1+a_n)\cdot n}{2}=\frac{(1+12)\cdot12}{2}=78$$
Задание 15
Высота равностороннего треугольника равна $$\frac{a\sqrt{3}}{2}.$$
Следовательно, сторона треугольника $$a=59\sqrt{3}\cdot\frac{2}{\sqrt{3}}=118.$$
Тогда периметр равностороннего треугольника равен $$3\cdot118=354.$$
Задание 16
Равные хорды отсекают равные дуги. Т.е. каждая сторона отсекает дугу $$\frac{360^{\circ}}{8}=45^{\circ}.$$
$$\angle ACE$$ опирается на дугу, отсекаемую 4 сторонами, т.е. $$180^{\circ},$$ но угол вписанный $$\Rightarrow\angle ACE=\frac{180^{\circ}}{2}=90^{\circ}$$
Задание 17
Треугольники MBN и АВС подобны, так как MN параллельна АС.
Из подобия:
$$\frac{MN}{AC}=\frac{12}{16}=\frac{3}{4}.$$ Это коэффициент подобия.
Площади подобных треугольников относятся как квадрат коэффициента подобия, то есть
$$\frac{S_{mbn}}{S_{abc}}=\frac{9}{16}.$$
Тогда $$S_{mbn}=\frac{9}{16}\cdot S_{abc}$$
$$S_{mbn}=\frac{9}{16}\cdot80=45$$
Задание 18
$$S=\frac{\pi R^2}{2}=\pi\cdot50\Rightarrow R^2=100\Rightarrow R=10\Rightarrow AB=20.$$
Опустим из G перпендикуляр на AB; пусть он пересекает $$AB=H.$$ Тогда $$AC=CE=x; EH=HB=y.$$
Или $$2x+2y=20\Rightarrow x+y=10.$$
Но DGHC - прямоугольник $$\Rightarrow DG=CH=x+y=10\Rightarrow DE=DG=10.$$
Задание 19
1) верно, через точку вне прямой можно провести параллельную этой прямой.
2) неверно, большая сторона треугольника должна быть меньше суммы двух других.
3) верно, т. к. если один из углов ромба равен 90°, то и остальные равны 90°.
4) неверно, есть тупоугольные треугольники, у которых центр описанной окружности вне его.
Задание 20
$$(\frac{x+3}{x^2-3x}+\frac{x-3}{x^2+3x})\cdot\frac{9x-x^3}{x^2+9}=\frac{(x+3)^2+(x-3)^2}{(x^2-9)x}\cdot\frac{x(9-x^2)}{x^2+9}=$$
$$=-\frac{x^2+6x+9+x^2-6x+9}{x^2+9}=-\frac{2(x^2+9)}{x^2+9}=-2$$
Задание 21
1) $$50\cdot3=150$$ (км) - прошел первый автомобиль до начала движения второго.
2) $$50 + 70 = 120$$ (км/ч) - скорость сближения автомобилей.
3) $$750 - 150 = 600$$ (км) - расстояние между автомобилями в момент начала движения второго.
4) $$\frac{600}{120} = 5$$ (ч) - двигались автомобили до встречи после выезда второго.
5) $$3 + 5 = 8$$ (ч) - затратил первый автомобиль до встречи со вторым.
6) $$50\cdot8 =400$$ (км) - на таком расстоянии от города а автомобили встретятся.
Задание 22
Для первой $$x_{0_1}=-\frac{-4a}{2}=2a,$$ для второй $$x_{0_2}=-\frac{8a}{-2}=4a$$
$$f(x_{0_1})=(2a)^2-4a\cdot2a+a=-4a^2+a$$
$$f(x_{0_2})=-(4a)^2+8a\cdot4a+4=16a^2+4$$
$$\left\{\begin{matrix} -4a^2+a>0\\ 16a^2+4>0 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -4a(a-\frac{1}{4})>0\\ a\in R \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a(a-\frac{1}{4})<0\\ a\in R \end{matrix}\right.\Leftrightarrow a\in(0;\frac{1}{4})$$
Вариант, когда оба отрицательные, не имеет решений.
Задание 23
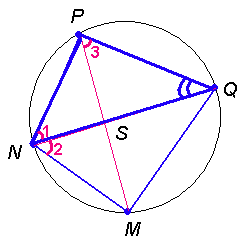
$$\angle2=\angle1$$ (NQ биссектриса)
$$\angle2=\angle3$$ (опираются на дугу MQ)
$$\Rightarrow\angle1=\angle3$$
$$\Delta NPQ\sim\Delta PSQ$$
$$\frac{NQ}{PQ}=\frac{PQ}{SQ}$$
$$NQ=\frac{PQ^2}{SQ}=\frac{86^2}{43}=172$$
$$NS=NQ-SQ=172-43=129$$
Задание 24
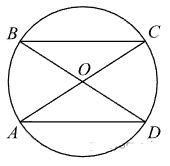
Вписанные углы ADB, CBD, ACB и DAC опираются на равные дуги, значит, они равны.
Получаем, что треугольники СOВ и AOD подобны по двум углам; их коэффициент подобия равен $$\frac{AO}{OC}$$
Поскольку AO = OC, эти треугольники равны, следовательно, AO = OC.
Задание 25
Пусть O - центр данной окружности, а Q - центр окружности, вписанной в треугольник ABC.
Точка касания M окружностей делит AC пополам.
Лучи AQ и AO - биссектрисы смежных углов, значит, угол OAQ прямой.
Из прямоугольного треугольника OAQ получаем:
$$AM^2=MQ\cdot MO$$
Тогда $$QM=\frac{AM^2}{OM}=\frac{9}{2}=4,5$$