ОГЭ математика 2023. Разбор варианта Алекса Ларина № 339.
Больше разборов на моем ютуб-канале
Задания 1-5
| Объекты | Жилой дом | Репа | Капуста | Кукуруза |
|---|---|---|---|---|
| Цифры |
Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?
| Двигатель | Дизельный | Бензиновый |
|---|---|---|
| Цена трактора (тыс. руб.) | 900 | 990 |
| Средний расход топлива (л/ч) | 5,5 | 7 |
| Стоимость топлива (руб./л) | 47 | 53 |
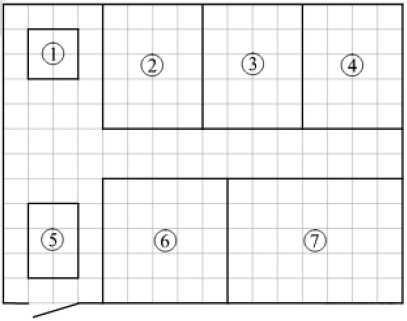
Прямо перед воротами предполагается построить жилой дом. Значит, дом отмечен цифрой 5.
Капустой планируется засеять поле, ближайшее к гаражу, значит, поле с капустой отмечено цифрой 2.
На поле рядом с картофелем планируется посеять кукурузу, следовательно, поле с кукурузой отмечено цифрой 6.
Оставшееся поле с репой отмечено цифрой 4.
Площадь одной клетки равна 2 · 2 = 4 м2. Значит, площадь пространства, которую необходимо засыпать гравием, равна
$$2\cdot12\cdot4=96$$ м2.
Чтобы засыпать 4 м2 гравием, требуется 0,2 м3 материала. Следовательно, понадобится $$\frac{96}{4}\cdot0,2=4,8$$ м3 гравия.
Значит, придётся купить 3 мешка с гравием.
Площадь всего участка равна
$$12\cdot16\cdot4=768$$ м2.
Площадь гаража равна
$$2\cdot2\cdot4=16$$ м2.
Площадь жилого дома равна
$$3\cdot2\cdot4=24$$ м2.
Площадь полей, засеянных капустой, морковью и репой, равна
$$5\cdot12\cdot4=240$$ м2.
Площадь полей, засеянных кукурузой и картофелем, равна
$$5\cdot12\cdot4=240$$ м2.
Таким образом, площадь территории, которая не занята постройками или полями, равна
$$786-16-24-240-240=248$$ м2.
Найдём расстояние между противоположными углами участка по теореме Пифагора:
$$\sqrt{24^2+32^2}=\sqrt{576+1024}=\sqrt{1600}=40$$ м.
Разность в стоимости тракторов равна 990 000 − 900 000 = 90 000 руб. Стоимость топлива за час работы трактора с дизельным двигателем равна 47 · 5,5 = 258,5 руб. Стоимость топлива за час работы трактора с бензиновым двигателем равна 53 · 7 = 371 руб. Следовательно, за час работы трактора Владимир экономит 371 − 258,5 = 112,5 руб. Таким образом, Владимир компенсирует разницу в стоимости между тракторами с разными двигателями через
$$\frac{90000}{112,5}=800$$ часов.
Задание 6
$$\frac{0,4}{1+\frac{1}{9}}=\frac{4}{10}\cdot\frac{9}{10}=0,36$$
Задание 7
1) $$\frac{a}{4}<\frac{c}{4}\quad$$ 2) $$-a<-c\quad$$ 3) $$a-32>c-31\quad$$ 4) $$a+13>c+10\quad$$
В ответе запишите номер правильного варианта ответа.1) $$a>c\Rightarrow \frac{a}{4}>\frac{c}{4}\Rightarrow$$ неверно
2) $$a>c\Rightarrow -a<-c\Rightarrow$$ верно
3) $$a>c\Rightarrow a-31>c-31$$, но $$a-32>с-31$$ не факт $$\Rightarrow$$ неверно
4) $$a+13>c+10\Rightarrow$$ верно
Примечание
В пункте 3: $$a-32>c-31\Rightarrow a>c+1$$. Это не гарантируется для любых $$a$$ и $$c$$. Например: $$1>0,9$$, но $$1<0,9+1$$. Поэтому 3 тоже неверно.
Задание 8
$$\frac{5\cdot3\cdot8}{5\cdot3\cdot8-8\cdot9}=\frac{120}{120-72}=\frac{120}{48}=\frac{5}{2}=2,5$$
Задание 9
Задание 10
$$P(A)=\frac{1}{5}=0,2$$
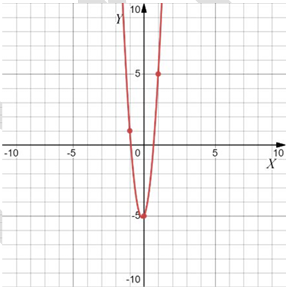
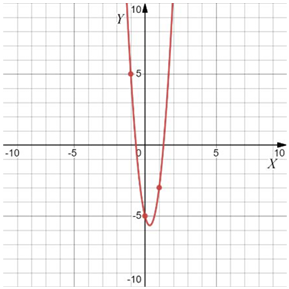
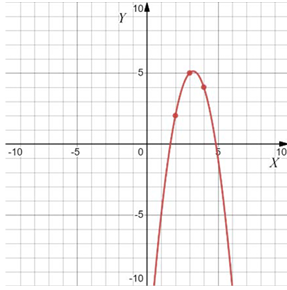
Задание 11
А)
Б)
В)
Г)
1) $$b=-7\quad$$ 2) $$b=13\quad$$ 3) $$b=2\quad$$ 4) $$b=-4\quad$$
А) ветви вверх, $$x_0<0\Rightarrow$$ т.к. $$x_0=-\frac{b}{2a}$$, $$a>0$$, то $$b>0$$
Б) ветви вниз $$(a<0), x_0<0\Rightarrow b<0$$
В) ветви вверх $$(a>0), x_0>0\Rightarrow b<0$$
Г) ветви вниз $$(a<0), x_0>0\Rightarrow b>0$$
При этом в пункте А имеем $$|a|$$ больше, чем $$|a|$$ в пункте Г. И при этом $$x_0$$ ближе, т.е. $$|b|$$ там меньше $$\Rightarrow$$ А-3; Г-2. Аналогично, Б-1; В-4.
Задание 12
$$h=\frac{3V}{S}=\frac{3\cdot40}{15}=8$$
Задание 13
1) $$(-\infty;1)\cup(\frac{5}{3};+\infty)\quad$$ 2) $$(-\infty;\frac{2}{3})\cup(2;+\infty)\quad$$ 3) $$(\frac{2}{3},2)\quad$$ 4) $$(1,\frac{5}{3})\quad$$
В ответе запишите номер правильного варианта ответа.$$(x - 1)(3x - 5) < 1$$
$$3x^2 - 5x - 3x + 5 < 1$$
$$3x^2 - 8x + 4 < 0$$
$$D = 64 - 4\cdot3\cdot3 = 64 - 48 = 16=4^2$$
$$x_1 = \frac{8 + 4}{6} = 2$$
$$x_2 = \frac{8 - 4}{6} = \frac{2}{3}$$
Чертим промежуток: ___+___2/3___-___2___+___.
Выбираем тот, что меньше нуля $$\Rightarrow (\frac{2}{3};2)\Rightarrow3$$
Задание 14
Прибыль каждый год увеличивалась на 10%, т.е. становилась равна 110% от прошлого года = 1,1.
Прибыль за 2000 год = 1000 млн рублей.
Прибыль за 2001 год:
$$1000\cdot1,1 = 1100$$ млн рублей
Прибыль за 2002 год:
$$1100\cdot1,1 = 1210$$ млн рублей
Прибыль за 2003 год:
$$1210\cdot1,1 = 1331$$ млн рублей
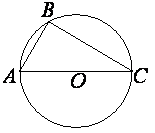
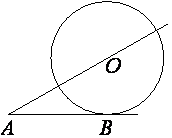
Задание 16
$$R = OB$$
По теореме Пифагора:
$$ОВ = \sqrt{АО^2 - АВ^2}$$
$$ОВ = \sqrt{97^2-65^2}=\sqrt{5184}=72$$
Задание 17
$$|AC|=\sqrt{(2-(-3))^2+(19-7)^2}=\sqrt{5^2+12^2}=13$$.
Средняя линия будет равна половине $$AC\Rightarrow 6,5$$.
Задание 18
Учтём, что $$FC=FK+KC\Rightarrow MR+JI=ED$$.
Получим: $$GM=MR\cdot\sqrt{3};\; IH=JI\cdot\sqrt{3}$$.
Пусть $$FC\cap MG=X;\; FC\cap IH=Y$$. Тогда $$XK=1,5MR;\; KY=1,5IJ$$.
Тогда $$S_{IMGH}=\frac{MG+IH}{2}\cdot XY=\frac{MR\cdot\sqrt{3}+JI\cdot\sqrt{3}}{2}(1,5MR+1,5IJ)=$$
$$=\frac{\sqrt{3}(MR+JI)}{2}\cdot1,5(MR+JI)=\frac{3\sqrt{3}}{4}ED^2=\frac{3\sqrt{3}}{4}\cdot(\frac{2\sqrt{2}}{\sqrt[4]{3}})^2=\frac{3\sqrt{3}}{4}\cdot\frac{4\cdot2}{\sqrt{3}}=6$$
Задание 19
2) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
3) В остроугольном треугольнике все углы острые.
1) неверно, легко себе представить разные по размеру квадраты, которые, естественно, будут иметь разные площади
2) неверно, утверждение может быть верно только для окружностей с одинаковыми радиусами.
3) верно, согласно определению остроугольного треугольника
Задание 20
$$\left\{\begin{matrix} \frac{8x-1}{15}-\frac{7x-2}{10}>\frac{1}{3}\\ (2x+1)^2\leq x(4x+3) \end{matrix}\right..$$
$$\frac{8x-1}{15}-\frac{7x-2}{10}>\frac{1}{3}\Rightarrow 16x-2-21x+6>10\Rightarrow -5x>6\Rightarrow x<-\frac{6}{5}$$
$$(2x+1)^2\leq x(4x+3)\Rightarrow 4x^2+4x+1\leq4x^2+3x\Rightarrow x\leq-1$$
Получим: $$\left\{\begin{matrix} x<-\frac{6}{5}\\ x\leq-1 \end{matrix}\right.\Rightarrow x\in(-\infty;-\frac{6}{5})$$
Задание 21
Из первого утверждения делаем вывод, что $$1$$ км состав проходит за $$1$$ минуту.
При движении в туннеле $$1$$ минуту состав тратит на вход и $$3-1=2$$ минуты на движение внутри.
Тогда длинна туннеля $$2$$ км.
Задание 22
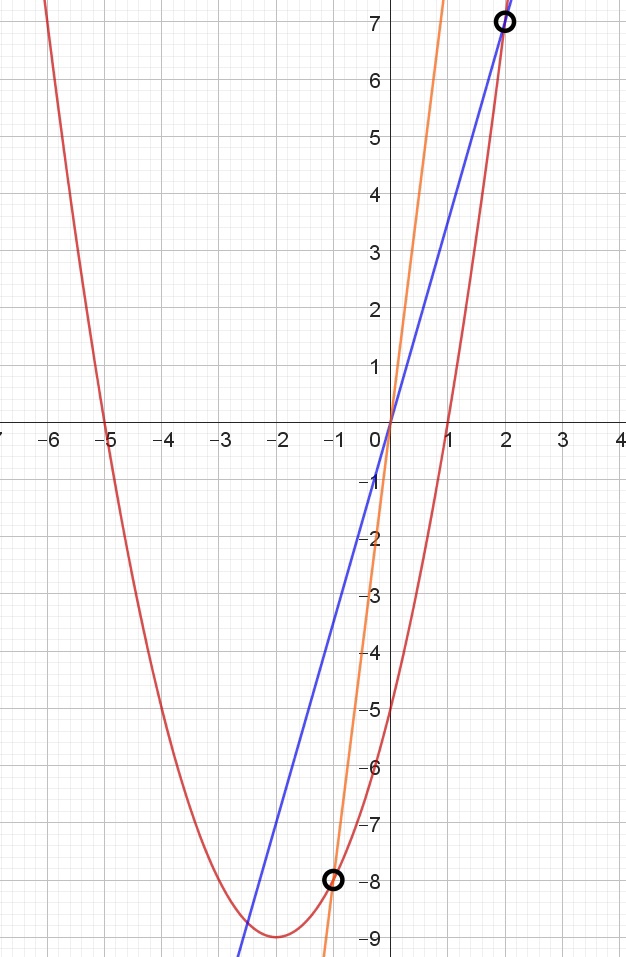
$$y=\frac{(x^2+3x-10)(x^2-1)}{x^2-x-2}=\frac{(x+5)(x-2)(x-1)(x+1)}{(x-2)(x+1)}=(x+5)(x-1)$$
При этом $$x\neq2\Rightarrow y\neq(2+5)(2-1)=7; x\neq-1\Rightarrow y\neq-8.$$
$$y=x^2+4x-5$$
$$x_0=-\frac{4}{2}=-2; y_0=(-2)^2+4\cdot(-2)-5=-9$$
$$y=ax$$ будет иметь одну точку, если
1) Пойдёт через $$(2;7)$$: $$7=a\cdot2\Rightarrow a=3,5$$
2) Пойдёт через $$(-1;-8)$$: $$-8=a\cdot(-1)\Rightarrow a=8$$
Задание 23
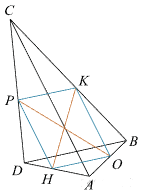
Пусть ABCD — данный четырёхугольник, O — середина стороны AB, K — середина стороны BC, P — середина стороны CD, H — середина стороны DA. Проведём диагонали AC и BD и отрезки OK, KP, PH и HO, последовательно соединяющие середины сторон четырёхугольника. Тогда, по свойству средней линии треугольника, отрезки OK и PH параллельны диагонали AC и равны её половине, а отрезки KP и HO параллельны диагонали BD и равны её половине. Поэтому OKPH — параллелограмм. А так как, по условию задачи, его диагонали KH и OP равны, то OKPH — прямоугольник, и угол OKP— прямой. Отсюда следует, что и угол между диагоналями AC и BD тоже прямой, и, следовательно, площадь четырёхугольника ABCD будет равна половине произведения его диагоналей, то есть $$\frac{1}{2}\cdot8\cdot5=20$$.
Задание 24
Построенная фигура действительно будет треугольником, так как отрезки соединяют половину вершин шестиугольника, то есть три точки.
Каждая из сторон полученного треугольника является основанием равнобедренного треугольника с боковыми сторонами, равными стороне правильного шестиугольника, и углом при вершине, равным внутреннему углу этого шестиугольника. Значит, указанные равнобедренные треугольники равны по двум сторонам и углу между ними. Следовательно, равны и их основания, являющиеся сторонами построенного равностороннего треугольника.
Задание 25
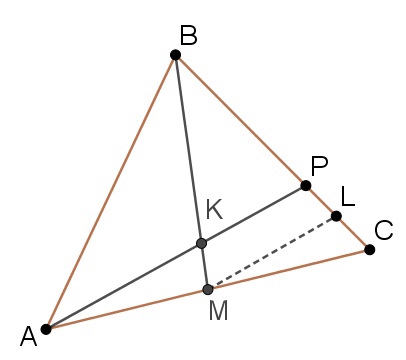
1) Пусть $$S_{ABC}=S$$. Тогда $$S_{ABM}=S_{BMC}=\frac{S}{2}$$.
2) Пусть $$ML||KP$$. По теореме Фалеса: $$\frac{AM}{MC}=\frac{PL}{LC}=\frac{1}{1}$$; $$\frac{BK}{KM}=\frac{BP}{PL}=\frac{4}{1}$$.
Тогда $$\frac{BP}{BC}=\frac{4}{6}=\frac{2}{3}$$.
3) $$\frac{S_{BKP}}{S_{BMC}}=\frac{BK\cdot BP}{BM\cdot BC}=\frac{4\cdot2}{5\cdot3}=\frac{8}{15}\Rightarrow S_{BKP}=\frac{8}{15}\cdot\frac{S}{2}=\frac{4}{15}S\Rightarrow\frac{S_{BKP}}{S_{ABC}}=\frac{4}{15}$$