ОГЭ математика 2023. Разбор варианта Алекса Ларина № 337.
Больше разборов на моем ютуб-канале
Задания 1-5
| Объекты | санузел | гостиная | детская | спальня | кухня |
|---|---|---|---|---|---|
| Цифры |
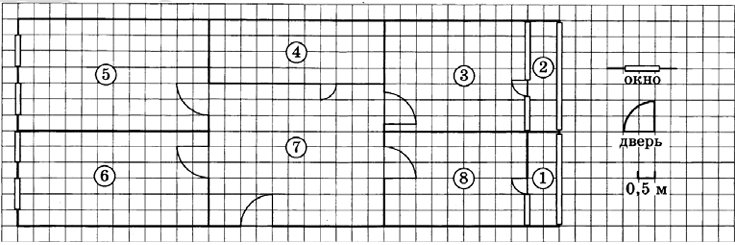
Вход в квартиру находится в прихожей (7). Напротив входа располагается санузел (4). В квартире есть две застеклённые лоджии (1 и 2).
Площадь кухни равна 18 квадратных метров ((6) $$S = 6\cdot0,5\cdot18\cdot0,5 = 18$$ м2), вход в детскую (5) расположен напротив входа в гостиную (3). Справа от входа — гостиная и спальня (8), а слева — кухня и детская.
Заполняем таблицу и записываем ответ.
Так как одна клетка равна 0,5 метра, а ширина лоджии = 6 клеток, следовательно остекление лоджии в спальне будет 3 метра.
Так как плитка 50 на 25 см, то есть 0,5 на 0,25 метров, значит, в одной клетке по 2 плитки.
Найдём площадь прихожей, она равна 99 клеток, или умножая на 2, 198 плиточек.
И, зная, что в одной упаковке 10 штук, мы $$\frac{198}{10}=19,8$$ упаковок, округляем, и получаем 20 упаковок.
Площадь спальни $$= 9\cdot6=54$$
Площадь кухни $$=12\cdot6=72$$
Пусть
72 - 100%
54 - x%
Тогда 54 = 75%
$$100\%-75\%=25\%$$
Задание 6
$$10\cdot\frac{1}{25}-12\cdot\frac{1}{5}=\frac{2}{5}-\frac{12}{5}=-2$$
Задание 7
1) $$\sqrt{3}\quad$$ 2) $$\sqrt{7}\quad$$ 3) $$\sqrt{8}\quad$$ 3) $$\sqrt{12}$$
В ответе запишите номер правильного варианта ответа.Учтём, что $$2,6=\sqrt{2,6^2}=\sqrt{5,76}$$; $$2,8=\sqrt{2,8^2}=\sqrt{7,24}\Rightarrow a=\sqrt{7}\Rightarrow 2$$
Задание 8
$$6\cdot45=270$$
Задание 10
В группе из 20 российских туристов французским языком владеют 3 (говорят только по-французски) + 2 (говорят по-французски и по-английски) = 5 человек.
Вероятность того, что случайно выбранный турист говорит по-французски = количество туристов, которые владеют французским языком : общее количество туристов:
$$P(A)=\frac{5}{20}=0,25$$
Задание 11
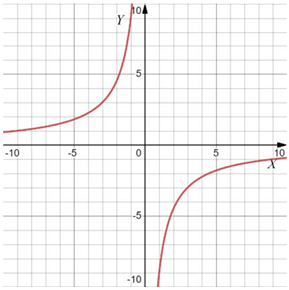 Б)
Б)
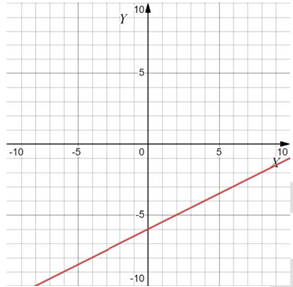 В)
В)
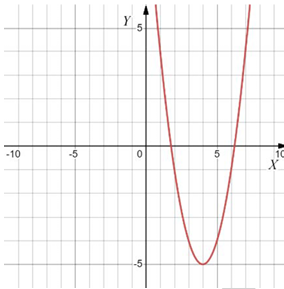 Г)
Г)

1) $$y = \frac{1}{2}x-6\quad$$ 2) $$y = x^2 - 8x + 11\quad$$ 3) $$y = -\frac{9}{x}\quad$$ 4) $$y = 2\sqrt{x}$$
А) гипербола $$\Rightarrow y=-\frac{9}{x}\Rightarrow 3$$
Б) линейная функция $$\Rightarrow y=\frac{1}{2}x-6\Rightarrow 1$$
В) парабола $$\Rightarrow y=x^2-8x+11\Rightarrow 2$$
Г) ветвь параболы $$\Rightarrow y=2\sqrt{x}\Rightarrow 4$$
Задание 12
$$R=\frac{a_n}{\omega^2}=\frac{64}{16}=4$$
Задание 13
1) $$(-\infty, 0)\cup(1, +\infty)\quad$$ 2) $$[0, 1]\quad$$ 3) $$(-\infty, 1)\quad$$ 4) $$(-\infty, 0]\cup[1, +\infty)$$
В ответе запишите номер правильного варианта ответа.$$-x^2+x\geq0\Rightarrow -x(x-1)\geq0\Rightarrow x(x-1)\leq0$$
$$x(x-1)=0\Rightarrow\left[\begin{matrix} x=0\\ x=1 \end{matrix}\right.$$
Пусть $$x(x-1)=f(x)$$:
$$f(-1)=-1\cdot(-2)>0$$
$$x\in[0;1]$$
Задание 14
Воспользуемся формулой арифметической прогрессии.
$$a_1=20$$ мест, $$d = 2$$ места.
$$S_n=\frac{2a_1+d(n-1)}{2}n=\frac{2\cdot20+2(12-1)}{2}\cdot12=372$$
Задание 15
Высоту h ромба можно найти из прямоугольного треугольника с гипотенузой $$c=54$$ (длина стороны ромба) и острым углом $$\alpha=180^{\circ}-150^{\circ}=30^{\circ}$$. Высота лежит против острого угла в 30°, значит, она будет в 2 раза меньше гипотенузы:
$$h=c\cdot\sin30^{\circ}=54\cdot\frac{1}{2}=27$$
Задание 16
Равные хорды отсекают равные дуги. Т.е. каждая сторона отсекает дугу $$\frac{360^{\circ}}{8}=45^{\circ}.$$
$$\angle ACE$$ опирается на дугу, отсекаемую 4 сторонами, т.е. $$180^{\circ},$$ но угол вписанный $$\Rightarrow\angle ACE=\frac{180^{\circ}}{2}=90^{\circ}$$
Задание 17
Согласно рисунку градусная мера центрального угла АОС равна $$45°+90° = 135°$$. Следовательно, дуга, на которую опирается вписанный в окружность угол АВС имеет градусную меру:
$$360°-135° = 225°$$.
По теореме о величине угла, вписанного в окружность, получаем, что градусная мера угла АВС:
$$\frac{225°}{2} = 112,5°$$.
Задание 18
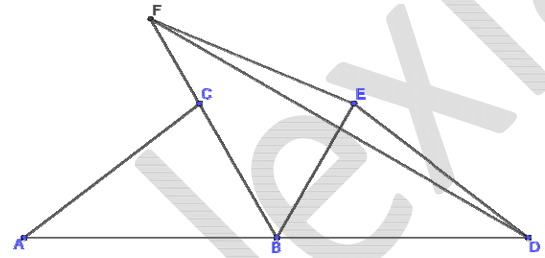
Из равенства треугольников ABC, DBE и FBE следует, что равны углы ABC, DBE и FBE, образующие развёрнутый угол, равный $$180°$$. Следовательно, каждый из этих углов равен
$$\frac{180°}{3} = 60°$$.
Угол DBF при вершине равнобедренного треугольника с основанием FD равен $$120°$$, так как составлен из двух углов DBE и FBE, каждый из которых равен $$60°$$. Значит, угол FDB при основании равнобедренного треугольника DBF:
$$\frac{180°-120°}{2} = 30°$$.
Задание 19
1) неверно, площадь трапеции равна половине высоты, умноженной на сумму оснований.
2) верно, это аксиома геометрии.
3) верно, это теорема планиметрии.
Задание 20
$$\left\{\begin{matrix} \frac{x+5}{y-3}=0\\ 2y^2+x^2-y=40 \end{matrix}\right.$$
$$\left\{\begin{matrix} \frac{x+5}{y-3}=0\\ 2y^2+x^2-y=40 \end{matrix}\right.\Rightarrow\left\{\begin{matrix} x+5=0\\ y-3\neq0\\ 2y^2+x^2-y=40 \end{matrix}\right.\Rightarrow\left\{\begin{matrix} x=-5\\ 2y^2+25-y=40\\ y\neq3 \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} x=-5\\ 2y^2-y-15=0\\ y\neq3 \end{matrix}\right.\Rightarrow\left\{\begin{matrix} x=-5\\ y=-2,5 \end{matrix}\right.$$
$$2y^2-y-15=0$$
$$D=1+120=121$$
$$y_1=\frac{1+11}{4}=3$$ - не подходит
$$y_2=\frac{1-11}{4}=-2,5$$
Задание 21
Задание 22
$$x = 0$$ – критическая точка, в ней подмодульное выражение меняет знак. Поэтому будем рассматривать два случая: когда $$x > 0$$ и $$x < 0$$.
1) При $$x > 0$$ функция примет такой вид
$$y=\frac{3,5x-1}{x-3,5x^2}=\frac{3,5x-1}{-x(-1+3,5x)}=-\frac{1}{x}$$
Графиком данной функции будет гипербола, к тому же, сразу определимся с ОДЗ. Т.к. у нас дана дробь, то ее знаменатель не может равняться нулю. Поэтому, икс не должен равняться 0 и 2/7 (х ≠ 0 и х ≠ 2/7).
Сразу найдем координаты точек, по которым будем чертить график.
| х | 0,5 | 1 | 2 |
| у | -2 | -1 | -0,5 |
Найдем координаты выколотой точки: если x ≠ 2/7, то y ≠ -3,5.
2) При $$х < 0$$ функция примет вид
$$y=\frac{-3,5x-1}{-x-3,5x^2}=\frac{-3,5x-1}{x(-1-3,5x)}=\frac{1}{x}$$
ОДЗ: х ≠ 0 и х ≠ -2/7.
Найдем координаты точек.
| х | -0,5 | -1 | -2 |
| у | -2 | -1 | -0,5 |
Найдем координаты выколотой точки: если x ≠ -2/7, то y ≠ -3,5.
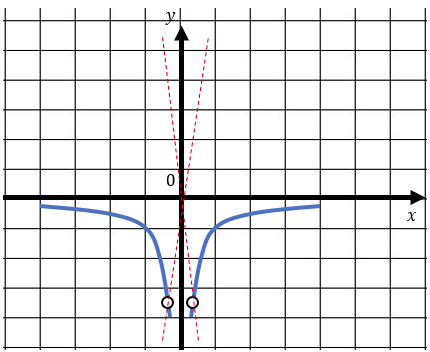
3) Теперь можно чертить график (синие кусочки гипербол).
$$y = kx$$ – прямая, проходящая под наклоном через начало координат (k – угловой коэффициент). И есть две потенциальные прямые, которые с нашим графиком не имеют общих точек (на координатной плоскости они отмечены красным цветом). Осталось лишь найти чему равен коэффициент k.
Обе прямые непременно должны проходить через выколотые точки. И логично предположить, что чтобы найти k надо в уравнение $$y = kx$$ подставить координаты этих выколотых точек. Это мы сейчас и сделаем.
Для точки (-2/7; -3,5)
$$-\frac{7}{2}=-\frac{2}{7}k;\; k=\frac{49}{4}=12,25$$
Для точки (2/7; -3,5)
$$-\frac{7}{2}=\frac{2}{7}k;\; k=-\frac{49}{4}=-12,25$$
И не стоит забывать, что при $$k = 0$$ прямая $$y = kx$$ превращается в прямую $$y = 0$$, которая совпадает с осью Ох. А, как известно, гипербола ее никогда не пересечет.
Таким образом, при $$k = ±12,25$$ и $$k = 0$$ прямая $$y = kx$$ не имеет с графиком общих точек.
Задание 23
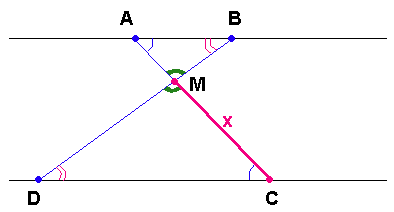
$$\Delta ABM\sim\Delta CDM$$
$$\frac{CM}{AM}=\frac{DC}{AB}$$
$$\frac{x}{48-x}=\frac{54}{18}$$
$$\frac{x}{48-x}=3$$
$$x=3(48-x)$$
$$x=144-3x$$
$$4x=144$$
$$x=36$$
Задание 24
$$∆AA_1C\sim ∆BB_1C$$ (по трем углам)
Пусть коэффициент подобия $$k$$
$$CB_1=c, A_1C = kc$$
$$BB_1 = b, AA_1 = kb$$
$$CB = a, CA = ka$$
В $$∆A_1CB_1$$ и $$∆ACB$$ две стороны подобны и углы между ними равны ⇒
$$∆A_1CB_1\sim ∆ACB$$
Задание 25
Из условия касания окружностей находим стороны треугольника $$O_1O_2O_3$$
$$O_1O_2=3, O_2O_3=5, O_1O_3=7$$
По теореме косинусов
$$O_1O_3^2=O_1O_2^2+O_2O_3^2-2O_1O_2\cdot O_2O_3\cdot\cos\angle O_1O_2O_3$$
$$49=9+25-30\cos\angle O_1O_2O_3$$
Откуда $$\cos\angle O_1O_2O_3=-\frac{1}{2}; \angle O_1O_2O_3=120^{\circ}$$.