ОГЭ математика 2019. Разбор варианта Алекса Ларина № 189.
Решаем ОГЭ 189 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №189 (alexlarin.com)
Решаем ОГЭ 189 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №189 (alexlarin.com)
Задание 1
Найдите значение выражения $$15*(\frac{1}{3})^{2}-3\frac{2}{3}$$
$$15*(\frac{1}{3})^{2}-3\frac{2}{3}=$$$$15*\frac{1}{9}-\frac{11}{3}=$$$$5*\frac{1}{3}-\frac{11}{3}=$$$$\frac{5-11}{3}=-2$$
Задание 2
Для квартиры площадью 62 кв. м заказан натяжной потолок белого цвета. Стоимость материалов с учётом работ по установке натяжных потолков приведена в таблице.
|
Цвет потолка |
Цена в рублях за 1 м2 (в зависмости от площали помещения) |
|||
|
до 10 м2 |
от 11 до 30 м2 |
от 31 до 60 м2 |
свыше 60 м2 |
|
|
белый |
1200 |
1000 |
800 |
600 |
|
цветной |
1350 |
1150 |
950 |
750 |
Какова стоимость заказа, если действует сезонная скидка в 5%?
Варианты ответа
Задание 3
На координатной прямой отмечены числа x, y, z
Какая из разностей отрицательна?
Варианты ответа
Учтем,что x
Задание 4
Найдите значение выражения $$\frac{26}{(5\sqrt{13})^{2}}$$
$$\frac{26}{(5\sqrt{13})^{2}}=$$$$\frac{26}{25*13}=\frac{2}{25}=0,08.$$
Задание 5
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,2 В до 0,8 В
1,2 B – в 9 часов, 0,8 B-19 ч. 19-9=10(ч)
Задание 6
Решите уравнение $$(5-x)^{2}=(11-x)^{2}$$
$$(5-x)^{2}=(11-x)^{2}$$ $$(5-x-(11-x))(5x+(11-x))=0$$ $$-6*(16-2x)-0$$ $$16-2x-0$$ $$x=8$$
Задание 7
В начале года число абонентов телефонной компании «Юг» составляло 1 миллион 200 тысяч человек, а в конце года их стало 1 миллион 584 тысячи человек. На сколько процентов увеличилось за год число абонентов этой компании?
1,2 млн.-100% 1,584 млн.-x% $$x=\frac{1,584 *100}{1,2}=1,32*100=132$$% 132-100=32%- изменение
Задание 8
На диаграмме показано содержание питательных веществ в творожных сырках. Определите по диаграмме содержание каких веществ превосходит 30%
*к прочему относятся вода, витамины и минеральные вещества
Варианты ответа
30% - сектор немного меньший, чем треть круга. Следовательно, более 30% составляют вещества из категории "прочее", то есть ответ будет под пунктом 4
Задание 9
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 2, но не дойдя до отметки 5.
С 2 до 5 сектор составляет $$\frac{5-2}{12}$$ круга. Т.е. и вероятность будет $$\frac{3}{12}=0,25$$
Задание 10
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
КОЭФФИЦИЕНТЫ
В таблице под каждой буквой укажите соответствующий номер.
| A | Б | В |
k>0-возрастает ,k<0-убывает,b>0- Oy пересекает над Ox, b<0-под Ox,тогда А2 Б3 В1.
Задание 11
Дана арифметическая прогрессия: 12, 9, 6,… . Какое число стоит в этой последовательности на 6-м месте?
$$a_{1}=12 $$. Найдем разность арифметической прогрессии: $$d=9-12=-3$$ Найдем 6ой член данной прогрессии: $$a_{6}=12-3(6-1)=12-15=-3.$$
Задание 12
Найдите значение выражения $$\frac{a-7b}{a}:\frac{7b^{2}-ab}{a^{2}}$$, при $$a=-9;b=6$$
$$\frac{a-7b}{a}:\frac{7b^{2}-ab}{a^{2}}=$$$$\frac{a-7b}{a}*\frac{a^{2}}{b(7b*a)}=$$$$-\frac{a}{b}=-\frac{-9}{6}=1,5.$$
Задание 13
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой $$t_{f}=1,8t_{c}+32$$ , где tc — температура в градусах Цельсия, tf — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует − 85 градусов по шкале Цельсия?.
$$t_{F}=1,8*(-85)+32=-153+32=-121$$
Задание 14
Укажите промежуток, являющийся решением системы неравенств $$\left\{\begin{matrix} 3x-9<0\\ 2-3x>-10 \end{matrix}\right.$$
Варианты ответа
- $$(-\infty ;+\infty )$$
- $$(-\infty ;4)$$
- $$(3 ;4 )$$
- $$(-\infty ;3 )$$
$$\left\{\begin{matrix}3x-9<0\\2-3x>-10\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}3x<9\\2+10>3x\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}x<3\\x<4\end{matrix}\right.\Rightarrow x\in (-\infty ;3 )$$
Данный ответ соответствует 4 варианту.
Задание 17
В треугольнике ABC BM – медиана и BH –высота. Известно, что AC=42 и BC=BM. Найдите AH.
$$BC=BM\Rightarrow \Delta BMC$$-равнобедренный $$\Rightarrow BH$$-медиана $$\Rightarrow MH=HC=\frac{1}{2}MC=\frac{1}{2}*\frac{1}{2}AC.$$ Т.е. $$MH=\frac{1}{4}*42=10,5 ; AM=21\Rightarrow AH=31,5.$$
Задание 19
Катеты прямоугольного треугольника равны $$3\sqrt{11}$$ и 1. Найдите синус наименьшего угла этого треугольника.
1)$$\angle A<\angle B$$, т.к. $$CB<AC$$
2)Найдем $$AB=\sqrt{(3\sqrt{11})^{2}+1^{2}}=\sqrt{100}=10.$$
3) $$\sin \angle A =\frac{CB}{AB}=\frac{1}{10}=0,1.$$
Задание 20
Какие из следующих утверждений верны?
1. верно 2. неверно( они равны) 3.верно
Задание 21
Найдите значение выражения: $$\frac{\sqrt{97+56\sqrt{3}}}{\sqrt{7+4\sqrt{3}}}*\sqrt{7+4\sqrt{3}}$$
$$\frac{\sqrt{97+56\sqrt{3}}}{\sqrt{7+4\sqrt{3}}}*\sqrt{7-4\sqrt{3}}$$ Выделим полный квадрат из $$97 +56\sqrt{3}$$ $$\left\{\begin{matrix}a^{2}+b^{2} =97\\2ab=56\sqrt{3}\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}a^{2}+b^{2}=97(1)\\ab=28 \sqrt{3}\end{matrix}\right.$$ $$28\sqrt{3}=2*2*7*\sqrt{3}$$, пусть a = 7 , тогда $$b=4\sqrt{3}.$$ Выполним выполнение равенства(1): $$7^{2}+(4\sqrt{3})^{2}=49+48=97$$ –верно, тогда $$97+56*\sqrt{3}=(7+4\sqrt{3})^{2}.$$ Получим: $$\sqrt{\frac{(7+4\sqrt{3})^{2}}{7+4\sqrt{3}}*(7-4\sqrt{3})}=$$$$\sqrt{(7+4\sqrt{3})(7-4\sqrt{3})}=\sqrt{49-48}=1.$$
Задание 22
Одновременно из пунктов А и С в пункт В отправляются два туриста. Через 4 часа они прибыли в пункт В. Второй турист каждый километр проходил на 3 минуты быстрее первого, так как путь от С до В на 4 км длиннее пути от А до В. Найдите скорость первого туриста.
Пусть x км –путь , тогда x+4 км-CB. Пусть y км\ч –скорость первого, z км\ч – скорость второго: $$\left\{\begin{matrix}\frac{x+4}{z}=4 & & \\\frac{x}{y}=4& & \\\frac{1}{y}-\frac{1}{z}=\frac{3}{60} & &\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}z=\frac{x+4}{4} & & \\y=\frac{x}{4} & & \\\frac{4}{x}-\frac{4}{x+4}=\frac{1}{20} & &\end{matrix}\right.$$ $$\frac{4x+16-4x}{x^{2}+4x}=\frac{1}{20}\Leftrightarrow$$ $$\frac{16}{x^{2}+4x}=\frac{1}{20}\Leftrightarrow$$ $$x^{2}+4x-320=0$$ $$\left\{\begin{matrix}x_{1}+x_{2}=-4 & & \\x_{1}x_{2}=-320& &\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}x_{1}=-20 & & \\x_{2}=16& &\end{matrix}\right.$$ $$y=\frac{16}{4}=4$$
Задание 23
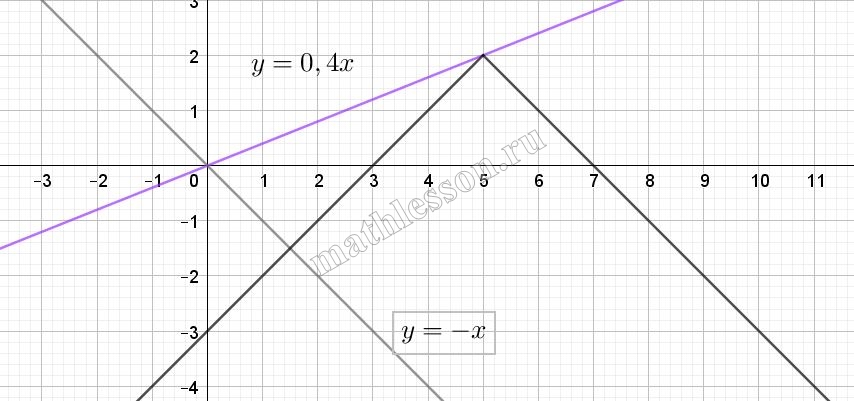
Найдите все значения k при которых прямая у = kx пересекает в двух точках ломаную, заданную условиями:$$\left\{\begin{matrix}x-3,x<5\\ 7-x,x\geq 5\end{matrix}\right.$$
$$y=\left\{\begin{matrix}x-3, x<5 & & \\7-x, x\geq 5& &\end{matrix}\right.$$
Начертим график данной функции :
При a>0 до момента , когда пройдет поезд (5;2) (прямая розового цвета) : $$2=5*k\Rightarrow k=0,4$$, то есть $$k\in [0; 0,4)$$.
При a<0, пока не станет параллельна (прямая серого цвета) прямой y=7-x, то есть $$a\in (-1; 0)$$ Итог (-1; 0,4)
Задание 24
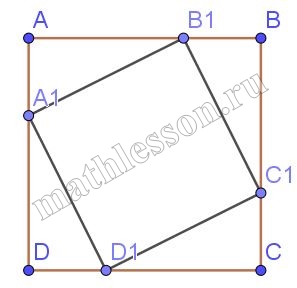
В квадрат, площадью 24 см2 вписан прямоугольник так, что на каждой стороне квадрата лежит одна вершина прямоугольника. Длины сторон прямоугольника относятся как 1:3. Найдите площадь прямоугольника.
1) Пусть $$\angle B_{1}C_{1}B=\alpha$$ , тогда $$\angle D_{1}C_{1}C=90-\alpha$$ , тогда $$\angle C_{1}D_{1}C=\alpha$$ .
Рассуждая аналогично получим :
$$\angle B_{1}C_{1}B=\angle C_{1}D_{1}C =\angle DA_{1}D_{1}=\angle A_{1}B_{1}A=\alpha$$ , следовательно , $$\angle B_{1}C_{1}B\sim \angle C_{1}D_{1}C \sim \angle DA_{1}D_{1}\sim \angle A_{1}B_{1}A$$
2)т.к. $$B_{1}C_{1}:C_{1}D_{1}=1:3$$,то пусть $$B_{1}B=x\Rightarrow CC_{1}=3x, BC_{1}=y$$, тогда $$CD_{1}=3y.$$
3) т.к. $$A_{1}B_{1}=C_{1}D_{1}$$ и $$B_{1}C_{1}=A_{1}D_{1}$$ и все треугольники подобны , то $$\Delta A_{1}B_{1}A=\Delta C_{1}D_{1}C$$ и $$\Delta B_{1}C_{1}B=\Delta DA_{1}D_{1}$$ следовательно $$DD_{1}=x$$
4) из п. 3 получили, что $$BC=y+3x$$ и $$CD=x+3y$$, тогда
$$y+3x=x+3y\Rightarrow x=y$$
5)$$AC=\sqrt{S_{ABCD}}=\sqrt{24}$$
$$\frac{BC_{1}}{CC_{1}}=\frac{1}{3}\Rightarrow$$$$ BC_{1}=\frac{\sqrt{24}}{4}\Rightarrow$$$$CC_{1}=\frac{3\sqrt{24}}{4}$$
6) $$\Delta B_{1}BC_{1}$$: $$B_{1}C_{1}=\sqrt{(\frac{\sqrt{24}}{4})^{2}+(\frac{\sqrt{24}}{4})^{2}}=\sqrt{3}.$$Тогда $$C_{1}D_{1}=3\sqrt{3}.$$
7)$$S_{A_{1}B_{1}C_{1}D_{1}}=3\sqrt{3}*\sqrt{3}=9$$
Задание 25
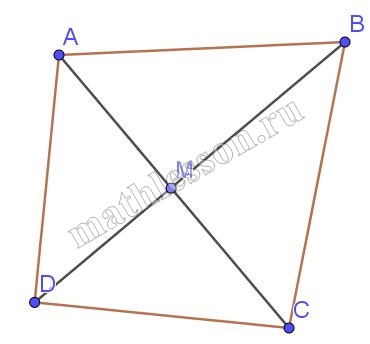
В выпуклом четырёхугольнике АВСD углы ACB и ADB равны. Докажите, что углы ABD и ACD также равны.
1) $$\angle AMD=\angle BMC$$(вертикальные) $$\angle ADB=\angle ACB$$(по условию) $$\Rightarrow \Delta AMB \sim \Delta BMC$$ и $$\frac{AM}{MB}=\frac{MD}{MC}(1)$$
2) $$\angle AMB=\angle DMC$$ (вертикальные) с учетом равенства (1) получим $$\Delta AMB \sim \Delta DMC\Rightarrow \angle ABD=\angle ACD$$
Задание 26
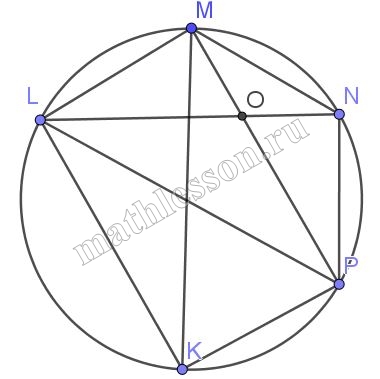
Точки K, L, M, N, P расположены последовательно на окружности радиуса $$2\sqrt{2}$$ . Найдите площадь треугольника KLM, если LM || KN, KM || NP, MN || LP, а угол LOM равен 45, где О – точка пересечения хорд LN и MP
1) $$LM\left | \right | KN\Rightarrow \angle LMK=\angle MKN$$(накрест лежащие)$$\Rightarrow \cup LK=\cup MN$$(вписанные углы равны)
$$MK \left | \right |NP\Rightarrow \angle MKN=\angle KNP\Rightarrow \cup KP=\cup MN=\cup LK.$$
$$LP\left | \right | MN\Rightarrow \angle LPM=\angle PMN\Rightarrow \cup LM=\cup NP.$$
2)Пусть $$\cup KL=\alpha$$ и $$\cup LM=\beta .$$
$$\angle LOM=\angle NOP$$(вертикальные) ,но т.к.
$$\cup LM=\cup NP$$, то $$\angle LOM-\frac{\cup LM+\cup PN}{2}=\beta =45$$
3)$$\Delta LPK : LK=2R \sin LPK= 2R \sin 45$$
$$\Delta LPM: LM=2R \sin LPM =2R \sin 22,5$$
$$S_{\Delta LKM}=\frac{1}{2} *LK*LM* \sin KLM=$$$$\frac{1}{2} *2R \sin 22,5 * \sin (90+22,5)=$$$$2R^{2}* \sin 22,5 * \cos 22,,5 * \sin 45=R^{2}* \sin^{2} 45=4$$