ОГЭ математика 2023. Разбор варианта Алекса Ларина № 338.
Больше разборов на моем ютуб-канале
Задания 1-5
| Объекты | гостиная | кухня | ванная комната | кладовая комната |
|---|---|---|---|---|
| Цифры |
| Счётчик | Однотарифный | Двухтарифный |
|---|---|---|
| Стоимость оборудования и монтажа (тыс. руб.) | 5,1 | 10 |
| Средняя потребляемая мощность (кВт) | 3,5 | 3,5 |
| Стоимость оплаты днём (06:00‐23:00) (руб./(кВт∙ч)) | 2 | 2 |
| Стоимость оплаты ночью (23:00‐06:00) (руб./(кВт∙ч)) | 2 | 1 |
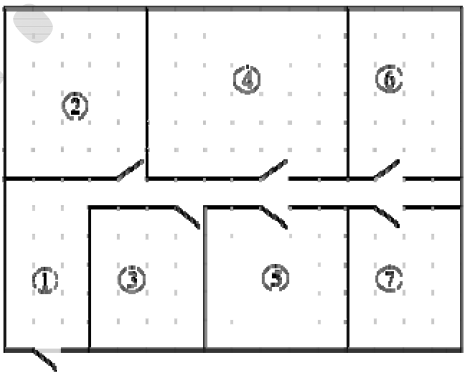
Поскольку гостиная занимает наибольшую площадь в квартире, можно заключить, что она обозначена на схеме цифрой 4.
Слева от гостиной находится кухня, следовательно, она обозначена цифрой 2.
Ванная комната находится напротив санузла, значит, ванная обозначена на схеме цифрой 7.
Кладовая комната расположена справа от коридора, следовательно, она обозначена цифрой 3.
Заметим, что, поскольку одна плитка имеет площадь 0,25 м2, чтобы выложить 1 м2 пола плиткой, понадобится 4 плитки.
Площадь санузла равна 6 · 4 = 24 м2. Площадь ванной равна 4 · 5 = 20 м2.
Теперь найдём, сколько упаковок плитки понадобилось: $$\frac{(24+20)\cdot4}{5}=35,2$$.
Следовательно, чтобы выложить пол в ванной комнате и санузле понадобится 36 упаковок плитки.
Сторона одной клетки равна 1 м. Значит, площадь гостиной равна: $$7\cdot6=42$$ м2.
Найдём расстояние между двумя ближайшими точками по прямой верхнего левого угла квартиры и нижнего правого угла квартиры по теореме Пифагора:
$$\sqrt{12^2+16^2}=\sqrt{144+256}=\sqrt{400}=20$$.
Разница в стоимости установки двухтарифного и однотарифного счётчиков равна $$10 − 5,1 = 4,9$$ тыс. руб.
День использования электроэнергии с однотарифным счётчиком стоит $$2 · 3,5 · 24 = 168$$ руб.
День использования электроэнергии с двухтарифным счётчиком стоит $$3,5 · 2 · 17 + 3,5 · 1 · 7 = 143,5$$ руб.
Разница в стоимости составляет $$168 − 143,5 = 24,5$$ руб.
Значит, экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного и однотарифного счётчиков через $$\frac{4900}{24,5}=200$$ дней.
Задание 6
$$\frac{9,5+8,9}{2,3}=\frac{18,4}{2,3}=8$$
Задание 7
1) $$a -b\quad$$ 2) $$a - c\quad$$ 3) $$b - c\quad$$ 4) $$c - b\quad$$
В ответе запишите номер правильного варианта ответа.1) $$a>b\Rightarrow a-b>0$$
2) $$a>c\Rightarrow a-c>0$$
3) $$b>c\Rightarrow b-c>0$$
4) $$b>c\Rightarrow c-b<0$$
Задание 10
$$P(A)=\frac{7}{7+13}=\frac{7}{20}=0,35$$
Задание 11
А) $$f(x) = x-\frac{1}{x-1}\quad$$ Б) $$f(x) = \frac{x+7}{x-5}+\frac{x-2}{x+6}\quad$$
В) $$f(x) = x^2+5x+7\quad$$ Г) $$f(x) = \sqrt{x}-\sqrt{x-3}\quad$$
1) $$a\in (-\infty;-29-\sqrt{727}]\cup(-8;-6)\cup[\sqrt{727}-29;3)\cup(5;+\infty)\quad$$
2) $$a\in [3;+\infty)\quad$$ 3) $$a\in (-\infty;-\frac{7}{2}]\quad$$ 4) $$a\in (-1;1)\quad$$
А) $$a-\frac{1}{a-1}\geq a+2-\frac{1}{a+1}\Leftrightarrow\frac{1}{a+1}-\frac{1}{a-1}-2\geq0\Leftrightarrow$$
$$\Leftrightarrow\frac{a-1-a-1-2a^2+2}{(a-1)(a+1)}\geq0\Leftrightarrow\frac{-2a^2}{(a-1)(a+1)}\geq0\Rightarrow$$
$$\Rightarrow\frac{a^2}{(a-1)(a+1)}\leq0\Rightarrow\left[\begin{matrix} a=0\\ (a-1)(a+1)<0 \end{matrix}\right.\left[\begin{matrix} a=0\\ a\in(-1;1) \end{matrix}\right.\Rightarrow a\in(-1;1)\Rightarrow 4$$
Б) $$\frac{a+7}{a-5}+\frac{a-2}{a+6}\geq\frac{a+9}{a-3}+\frac{a}{a+8}\Leftrightarrow$$
$$\Leftrightarrow1+\frac{12}{a-5}+1-\frac{8}{a+6}\geq1+\frac{12}{a-3}+1-\frac{8}{a+12}\Rightarrow 1$$, т.к. там есть $$-6;3;5$$
В) $$a^2+5a+7\geq(a+2)^2+5(a+2)+7\Rightarrow a^2+5a+7\geq a^2+4a+4+5a+17\Rightarrow$$
$$\Rightarrow-4a\geq14\Rightarrow a\leq-\frac{7}{2}\Rightarrow 3$$
Задание 12
Выразим $$b$$ из предложенной формулы. Для этого сначала выразим чему равно делимое $$a + b - c$$, а после этого выразим значение самого катета $$b$$:
$$a + b - c = 2r$$
$$b = 2r + c - a$$
Подставим известные данные в формулу и получим результат:
$$b = 2 ⋅ 1,2 + 6,8 - 6 = 3,2$$
Задание 13
1) $$[3,6]\quad$$ 2) $$[-6,-3]\quad$$ 3) $$(-\infty,3]\cup[6,+\infty)\quad$$ 4) $$(-\infty,-6]\cup[-3,+\infty)\quad$$
В ответе запишите номер правильного варианта ответа.$$\left\{\begin{matrix}6x+18\leq0\\ x+8\geq2\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}6x \leq -18\quad|:6 \\ x\geq 2-8 \end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}x \leq -3\\ x\geq -6 \end{matrix}\right.$$ Получаем, что $$x \in [-6;-3]\Rightarrow 2$$
Задание 14
Эта задача решается просто, учитывая, что сумма любой пары дней, отстоящих по счёту на одинаковое расстояние от начала и конца, одинакова, получаем:
$$\frac{270}{90}$$ = 3 пары дней, или 6 дней.
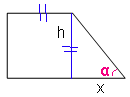
Задание 15
$$\tg\alpha=\frac{h}{x}$$
$$x=h:\tg\alpha$$
$$h = 55$$
$$x = 55 : \frac{1}{2}=55\cdot\frac{2}{1} = 110$$
Основание $$= 55 + х = 55 + 110 = 165$$
Задание 16
Поскольку на окружности дуга KN определяет угол KON, равный 180°, то на угол КОМ, при вычитании из него градусной меры дуги MN, равной 124°, остаётся всего градусная мера в:
$$180° - 124° = 56°$$
Задание 17
Пусть $$A(0;0)\Rightarrow B(2;3); C(2;-3)$$. Пусть M - середина BC $$\Rightarrow M_x=\frac{2+2}{2}=2; M_y=\frac{3+(-3)}{2}=0\Rightarrow M(2;0)$$.
Тогда $$|AM|=\sqrt{(2-0)^2+(0-0)^2}=\sqrt{2^2}2$$.
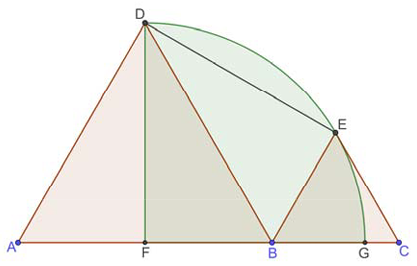
Задание 18
1) То что FGED - четверть окружности с центром F и радиусом FD=FG, дает то, что FD ⟂ FG, а значит FD - высота в ∆ADB (она же медиана в равностороннем треугольнике).
2) Если площадь четверти круга равна $$9\pi$$, то площадь всего круга равна $$4\cdot9\pi = 36\pi$$
Но площадь круга $$S = πR² = 36π$$, откуда $$R² = 36$$ и $$FD = R = 6$$
3) высота в равностороннем треугольнике $$h = \frac{a\sqrt{3}}{2}$$
(если не помним, то из ∆DFB - прямоугольный. По теореме Пифагора:
$$FD² = DB² - FB², FB=\frac{DB}{2}$$
$$FD² = DB² - (\frac{DB}{2})² = \frac{3DB²}{4}$$ и $$FD = \frac{DB\sqrt{3}}{2}$$)
Таким образом $$DB = \frac{2FD}{\sqrt{3}} = 2\cdot\frac{6}{\sqrt{3}} = \frac{12}{\sqrt{3}} = 4\sqrt{3}$$
4) Так как ∆BEC равносторонний, то ∠EBC = 60˚ => ∠ABE = 180˚ - ∠EBC = 120˚ (смежный угол)
5) Рассмотрим ∆FBE: $$FE = 6; FB = \frac{DB}{2} = 2\sqrt{3}$$ и $$∠FBE = 120˚$$
По теореме косинусов $$FE² = FB² + BE² - 2FB\cdot BE\cdot \cos(∠FBE)$$
$$36 = 12 + BE² - 2\cdot2\sqrt{3}\cdot(-0,5)\cdot BE$$
$$BE² + 2\sqrt{3}BE - 24 = 0$$
$$D = 12 + 4\cdot24 = 108 = 3\cdot36$$
$$ВЕ = \frac{-2\sqrt{3} + 6\sqrt{3}}{2} = 2\sqrt{3}$$ (второй корень отрицательный и не подходит)
Получили BE = FB
6) Рассмотрим ∆DBF и ∆DBE: DB=DB (общая), FB=BE, и ∠FBD = ∠DBE = 60˚ => ∆DBF = ∆DBE и тогда DE = DF = 6
Задание 19
1) неверно, площадь трапеции равна половине высоты, умноженной на сумму оснований.
2) верно, это аксиома геометрии.
3) верно, это теорема планиметрии.
Задание 20
$$(1-\sqrt{2})x\geq2-2\sqrt{2}$$
Учтём, что $$1-\sqrt{2}<0\Rightarrow x\leq\frac{2-2\sqrt{2}}{1-\sqrt{2}}\Rightarrow x\leq\frac{2(1-\sqrt{2})}{1-\sqrt{2}}\Rightarrow x\leq2$$
Задание 21
Процентная концентрация раствора (массовая доля) равна $$\omega=\frac{m_{в-ва}}{m_{р-ра}}\cdot100\%$$. Пусть масса получившегося раствора $$2m$$. Таким образом, концентрация полученного раствора равна:
$$\omega=\frac{0,18m+0,22m}{2m}\cdot100\%=\frac{0,4}{2}\cdot100\%=20\%$$
Задание 22
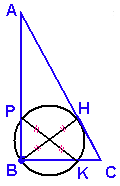
Задание 23
Прямоугольный треугольник KPB с гипотенузой PK вписан в окружность. Следовательно, PK является диаметром окружности. (по теореме об описанной окружности).
$$PK=BH=11$$
Задание 24
Точка I равноудалена от точек A и B, поэтому эта точка лежит на серединном перпендикуляре к отрезку AB. Аналогично, точка J лежит на серединном перпендикуляре к отрезку AB. Значит, прямая, содержащая точки I и J, является серединным перпендикуляром к отрезку AB. Следовательно, прямые IJ и АВ перпендикулярны.
Задание 25
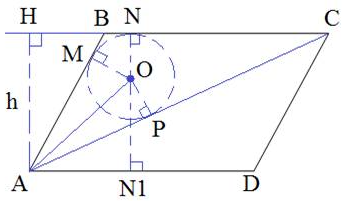
Окружность вписана в треугольник ABC с радиусами $$OM=ON=OP$$ и перпендикулярными сторонам AB, BC, AC соответственно. По теореме об отрезках касательных, имеем:
$$MB=BN, AM=AP, CN=CP$$.
Пусть $$BM=BN=x$$, а $$CN=CP=y$$. Тогда $$BC=AD=x+y$$. Отрезок $$NN_1=AH=8+6=14$$. Рассмотрим прямоугольный треугольник AMO. По теореме Пифагора найдем сторону AM:
$$AM=\sqrt{AO^2-OM^2}=\sqrt{10^2-6^2}=8$$
Значит, $$AP=AM=8$$. Найдем величину $$x+y$$ из формулы площади треугольника ABC:
$$S_{ABC}=\frac{1}{2}(x+y)\cdot14$$
Эту же площадь можно вычислить как
$$S_{ABC}=p\cdot r$$,
где $$p=\frac{1}{2}\cdot(AB+BC+AC)=8+x+y$$ - полупериметр треугольника ABC; $$r=6$$ – радиус вписанной окружности. Приравниваем площади, получаем уравнение:
$$7\cdot(x+y)=(x+y+8)\cdot6$$
$$7(x+y)-6(x+y)=48$$
$$x+y=48$$
Значит, $$BC=AD=48$$ и площадь параллелограмма, равна:
$$S_{ABCD}=AD\cdot H=48\cdot14=672$$