ОГЭ математика 2019. Разбор варианта Алекса Ларина № 205.
Решаем ОГЭ 205 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина № 205 (alexlarin.com)
Решаем ОГЭ 205 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина № 205 (alexlarin.com)
Задание 1
Найдите значение выражения $$4\frac{7}{8}:(2\frac{3}{4}+1\frac{10}{19})$$
$$4\frac{7}{8}:(2\frac{3}{4}+1\frac{10}{19})=$$$$\frac{39}{8}:(\frac{11}{4}+\frac{29}{19})=$$$$\frac{39}{8}:\frac{11*19+4*29}{4*19}=$$$$\frac{39}{8}*\frac{4*19}{209+116}=$$$$\frac{39}{8}*\frac{4*19}{325}=$$$$\frac{741}{2*325}=1,14$$
Задание 2
Для квартиры площадью 90 кв. м заказан натяжной потолок белого цвета. Стоимость материалов с учётом работ по установке натяжных потолков приведена в таблице
| Цвет потолка | Цена (в руб.) за 1 кв. м (в зависимости от площади помещения | |||
| до 10 кв. м | от 11 до 30 кв. м | от 31 до 60 кв. м | свыше 60 кв. м | |
| Белый | 1500 | 1250 | 1050 | 700 |
| Цветной | 1650 | 1400 | 1200 | 850 |
Задание 3
Значение какого из данных выражений положительно, если известно, что a > 0, b < 0?
Варианты ответа
- ab
- (a − b)b
- (b − a)b
- (b − a)a
Пусть a=2 ; b=-1
- $$ab=2*(-1)=-2<0$$
- $$(a-b)b=(2-(-1))*(-1)=3*(-1)<0$$
- $$(b-a)b=((-1)-2)*(-1)=(-3)(-1)>0$$
- $$(b-a)a=((-1)-2)*2=(-3)*2<0$$
Положителен только варинат под номером 3
Задание 4
Найдите значение выражения $$\frac{\sqrt{450}\sqrt{24}}{\sqrt{20}}$$
Варианты ответа
- $$60$$
- $$6\sqrt{5}$$
- $$6\sqrt{10}$$
- $$6\sqrt{15}$$
$$\frac{\sqrt{450}*\sqrt{24}}{\sqrt{20}}=$$$$\sqrt{\frac{450*24}{20}}=$$$$\sqrt{45*12}=3*2\sqrt{5*3}=6\sqrt{15}$$, что соответствует 4 варианту ответа
Задание 5
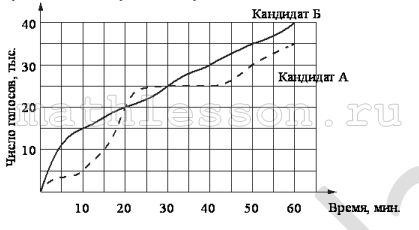
На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 40 минут дебатов?
За кандидата A : 25 тысяч; за Б :30 тысяч; всего за обоих : 25+30=55 тысяч
Задание 6
Решите уравнение $$5x-5(3-x)=x^{2}+10$$
$$5x-5(3-x)=x^{2}+10\Leftrightarrow$$$$5x-15+5x-x^{2}-10=0\Leftrightarrow$$$$-x^{2}+10x-25=0\Leftrightarrow$$ $$x^{2}-10x+25=0\Leftrightarrow$$ $$(x-5)^{2}=0\Leftrightarrow$$ $$x=5$$
Задание 7
Закупив подарочные наборы на оптовом складе, магазин стал продавать их по цене на 40% больше закупочной. Перед Новым годом цена наборов была снижена на 30%. Какая цена меньше: та, по которой магазин закупил подарочные наборы, или предновогодняя – и на сколько процентов?
Пусть x - закупочная цена , тогда $$(1+\frac{40}{100})x=1,4x$$ - цена продажи . С учетом снижения цены: $$1,4x*(\frac{100-30}{100})=0,98x$$ - предновогодняя. Получаем, что ниже предновогодняя на 2% (0,98 - 98%)
Задание 8
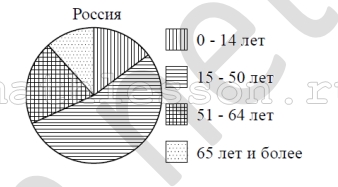
На диаграмме показан возрастной состав населения России. Определите по диаграмме, какая из возрастных категорий самая многочисленная.
Варианты ответа
- 0 – 14 лет
- 15 – 50 лет
- 51 – 64 лет
- 65 лет и более
Самая многочисленная категория населения 15-50 лет, что соответствует 2 варианту ответа
Задание 9
В среднем из 120 карманных фонариков, поступивших в продажу, шесть неисправны. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
Если 6 неисправны, то 120-6=114 исправны. Тогда вероятность получить исправный: $$P=\frac{114}{120}=0,95$$
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают.
ФОРМУЛЫ
- $$y=x^{2}+2$$
- $$y=-\frac{6}{x}$$
- $$y=\frac{1}{2}x$$
A – обратная пропорциональность ($$y=\frac{k}{x}$$)$$\Rightarrow 2$$
Б – линейная функция ($$y=kx$$)$$\Rightarrow 3$$
B - квадратичная функция ($$y=ax^{2}+b$$)$$\Rightarrow 1$$
Задание 11
Последовательность (an) задана условиями a1=-3, an+1=an+3. Найдите a10.
Дана арифметическая прогрессия, найдем ее разность: $$d=a_{n+1}-a_{n}=a_{n}+3-a_{n}=3$$ Найдем её 10-ый член: $$a_{n}=a_{1}+d(n-1)$$$$\Rightarrow$$ $$a_{10}=-3+3(10-1)=24$$
Задание 12
Найдите значение выражения $$\frac{a^{2}-4b^{2}}{3a^{2}}*\frac{a}{3a+6b}$$, при $$a=\sqrt{125}, b=\sqrt{245}$$
$$\frac{a^{2}-4b^{2}}{3 a^{2}}*\frac{a}{3a+6b}=$$$$\frac{(a-2b)(a+2b)}{3a*3(a+2b)}=$$$$\frac{a-2b}{9a}=\frac{\sqrt{125}-2\sqrt{245}}{9*\sqrt{125}}=$$$$\frac{5\sqrt{5}-2*7\sqrt{5}}{9*5\sqrt{5}}=$$$$\frac{-9\sqrt{5}}{9*5\sqrt{5}}=-\frac{1}{5}=-0,2$$
Задание 13
Период колебания математического маятника (в секундах) приближённо можно вычислить по формуле $$T=2\sqrt{l}$$ , где l — длина нити в метрах. Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 12 секунд.
Выразим значение длины из формулы: $$T= 2\sqrt{l}$$$$\Leftrightarrow$$ $$\sqrt{l}=\frac{T}{2}$$$$\Leftrightarrow$$ $$l=\frac{T^{2}}{4}$$ Найдем значение длины: $$l=\frac{12^{2}}{4}=36$$
Задание 14
Укажите неравенство, которое не имеет решений.
- $$x^{2}-169\leq 0$$
- $$x^{2}+169\geq 0$$
- $$x^{2}-169\geq 0$$
- $$x^{2}+169\leq 0$$
- $$x^{2}-169\leq 0$$$$\Rightarrow$$ $$x \in [-13,13]$$
- $$x^{2}+169\geq 0$$$$\Rightarrow$$ $$x \in R$$
- $$x^{2}-169\geq 0$$$$\Rightarrow$$ $$x \in (-\infty , -13]\cup [13,+\infty )$$
- $$x^{2}+169\leq 0$$$$\Rightarrow$$ $$x \in \varnothing$$ (так как $$x^{2}$$ - число неотрицательное, и ва сумме с положительным никак не может быть меньше 0)
Задание 15
Лестница соединяет точки A и B и состоит из 25 ступеней. Высота каждой ступени равна 14 см, а длина – 48 см. Найдите расстояние между точками A и B (в метрах).
Найдем диагональ ступеньки: $$\sqrt{14^{2}+48^{2}}=50$$ см. Найдем AB: $$25*50$$ см. $$\Rightarrow$$ $$\frac{25*50}{100}=12,5$$ метров
Задание 16
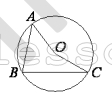
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=65° и ∠OAB=10°. Найдите угол BCO. Ответ дайте в градусах.
1) $$\Delta ABO$$ - равнобедренный $$\Rightarrow$$ $$\angle OAB=\angle ABO=10$$$$\Rightarrow$$ $$\angle OBC=65-10=55$$
2) $$\Delta OBC$$ – равнобедренный $$\Rightarrow$$ $$\angle BCO=\angle OBC=55$$
Задание 17
Основания трапеции равны 11 и 16. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Меньший - половина меньшего основания (средняя линия в треугольнике) Больший – половина большого основания или $$\frac{16}{2}=8$$
Задание 18
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке Е. Найдите периметр параллелограмма, если BЕ=10, CЕ=7
1) $$BC=AD=10+7=17$$
2) $$\angle BAE=\angle EAD$$ ( AE - биссектриса ); $$\angle EAD=BEA$$ (накрест лежащие) $$\Rightarrow$$ $$\angle BEA=\angle BAE\Rightarrow$$ $$AB=BE=10=CD$$
3) $$P_{ABCD}=(17+10)*2=54$$
Задание 19
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
Очевидно по рисунку, что расстояние от А до середины CB составит 3 клетки или 3 сантиметра
Задание 20
Какие из следующих утверждений верны?
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
1. Нет - возможна трапеция 2. Верно 3. Верно (так как угла в них всегда будут 45,45,90)
Задание 21
Решите неравенство $$(\frac{2x+1}{5-x})^{2}\leq \frac{1}{25}$$
$$(\frac{2x+1}{5-x})^{2}\leq \frac{1}{25}$$$$\Leftrightarrow$$ $$(\frac{2x+1}{5-x})^{2}-(\frac{1}{5})^{2}\leq 0$$$$\Leftrightarrow$$ $$(\frac{2x+1}{5-x}-\frac{1}{5})(\frac{2x+1}{5-x}+\frac{1}{5})\leq 0$$$$\Leftrightarrow$$ $$\frac{10x+5-5+x}{5(5-x)}*\frac{10x+5+5-x}{5(5-x)}\leq 0$$$$\Leftrightarrow$$ $$\frac{11x*(9x+10)}{25(5-x)^{2}}\leq 0$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}x(9x+10)\leq 0\\5-x\neq 0\end{matrix}\right.$$$$\Leftrightarrow$$ $$x \in [-\frac{10}{9};0]$$
Задание 22
Скорость автомобиля по ровному участку на 5 км/ч меньше, чем скорость под гору, и на 15 км/ч больше, чем скорость в гору. Дорога из A в B идет в гору и равна 100 км. Определить скорость автомобиля по ровному участку, если расстояние от A до B и обратно он проехал за 1 ч 50 мин.?
Пусть x км\ч – скорость по ровному участку , тогда x+5 км\ч –под гору; x-15 км\ч-в гору
Время в гору: $$\frac{100}{x-5}$$; под гору: $$\frac{100}{x+5}$$;
Получим: $$\frac{100}{x-15}+\frac{100}{x+15}=1\frac{50}{60}=\frac{11}{6}$$ $$100(\frac{x+5+x-15}{(x-15)(x+6)})=\frac{11}{6}$$$$\Leftrightarrow$$ $$6*100(2x-10)=11(x^{2}-10x-75)\Leftrightarrow$$$$11x^{2}-110x-825=1200x-6000\Leftrightarrow$$$$11x^{2}-1310x+5175=0$$
$$D=1716100-227700=1220^{2}$$
Тогда в ответ запишем 115
Задание 23
Постройте график функции $$y=1-\frac{2x^{4}-x^{3}}{2x^{2}-x}$$ и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
$$y=1-\frac{2x^{4}-x^{3}}{2x^{2}-x}=1-\frac{x^{3}(2x-1)}{x(2x-1)}$$$$\Rightarrow$$ $$y=\left\{\begin{matrix}1-x^{2}\\x\neq 0\\2x-1\neq 0\end{matrix}\right.\Leftrightarrow$$ $$y=\left\{\begin{matrix}1-x^{2}\\x \neq 0\\x\neq 0,5\end{matrix}\right.$$
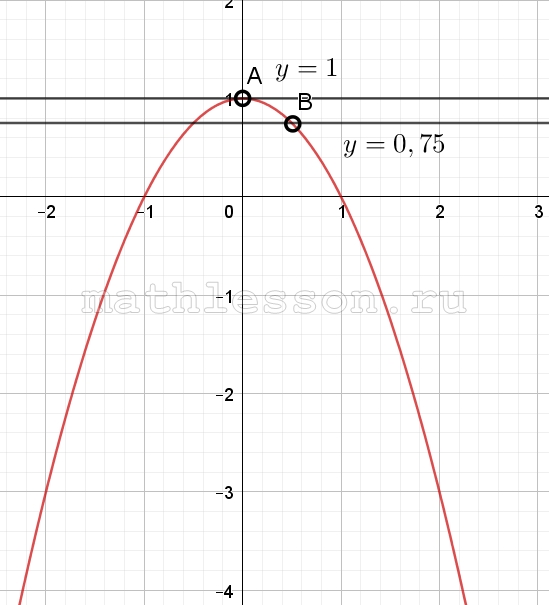
Построим график данной функции (не забудем отметить пустыми точка (A и B) имеющиеся ограничения:
Видим, что прямая всегда будет пересекать в двух точках параболы (на области значений параболы) кроме тех случаев, когда она пройдет через точку А или В: $$m \in (-\infty;0,75)\cup (0,75; 1)$$
Задание 24
Боковая сторона неравнобедренной трапеции равна 12 см и образует с большим основанием угол 60. Основания трапеции равны 16 см и 40 см. Найдите площадь трапеции.
1) Пусть $$BH\perp AD\Rightarrow$$ из $$\Delta ABH$$: $$BH=AB \sin A=12*\frac{\sqrt{3}}{2}=4\sqrt{3}$$
2) $$S_{ABCD}=\frac{BC+AD}{2}*BH=$$$$\frac{16+40}{2}*4\sqrt{3}=112\sqrt{3}$$
Задание 25
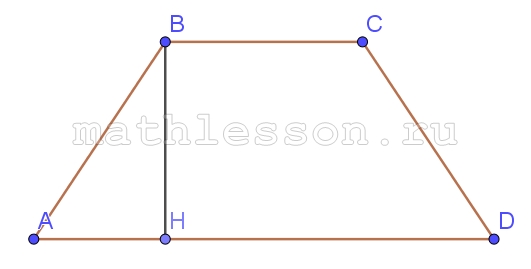
На стороне BC квадрата ABCD взята точка Р. Докажите, что площадь квадрата вдвое больше площади треугольника AРD.
1) Пусть $$PH\mid AD\Rightarrow$$ $$PHDC$$ - прямоугольник $$\Rightarrow$$ $$PH=CD$$
2) $$S_{ABCD}=AB*BC$$; $$S_{ABCD}=\frac{1}{2}*AD*PH$$; $$PH=CD=AB$$; $$AD=BC\Rightarrow$$ $$S_{ABCD}=\frac{1}{2} *AB*BC=\frac{1}{2} S_{ABCD}$$
Задание 26
Продолжение сторон AD и BC выпуклого четырехугольника ABCD пересекаются в точке M, а продолжения сторон AB и CD – в точке O. Отрезок MO перпендикулярен биссектрисе угла AOD. Найдите отношение площадей треугольника AOD и четырехугольника ABCD, если АО = 12, ОD = 8, CD = 2.
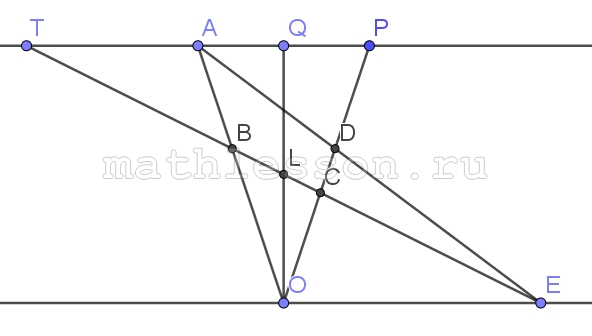
A) 1) Пусть C между O и D. Проведем через $$A n\left | \right |OM$$: $$P=CD\cap n$$; $$Q=OL\cap n$$; $$T=CB\cap n$$
2) $$OQ\perp OM$$; $$OM\left | \right |AP\Rightarrow$$ $$OQ\perp AP\Rightarrow$$ OQ - высота и биссектриса $$\Rightarrow$$ $$\Delta AOP$$ – равнобедренны $$\Rightarrow$$ $$OP=OA=12$$; $$PD=OP-PD=12-8=4$$
3) $$\Delta MDO\sim \Delta ADP$$: $$\frac{OM}{AP}=\frac{OD}{DP}\Rightarrow$$ $$OM=\frac{AP*OD}{DP}=2 AP$$; $$\Delta PCT\sim OCM$$: $$\frac{OM}{PT}=\frac{OC}{PC}\Rightarrow$$ $$PT=\frac{MO*PC}{OC}=MO=2 AP$$$$\Rightarrow$$ $$AT=AP$$; $$OM=2 AT$$; $$\Delta MBD\sim \Delta TBA$$: $$\frac{OB}{AB}=\frac{MO}{AT}=\frac{2}{1}$$
4) Пусть $$S_{AOD}=S\Rightarrow$$ $$S_{BOC}=\frac{OB}{AO}*\frac{OC}{OD}S=$$$$\frac{2}{3}*\frac{6}{8}S=\frac{S}{2}$$$$\Rightarrow$$ $$S_{ABCD}=S_{AOD}-S_{BOC}=\frac{S}{2}\Rightarrow$$ $$\frac{S_{AOD}}{S_{ABCD}}=\frac{S}{\frac{S}{2}}=\frac{2}{1}$$
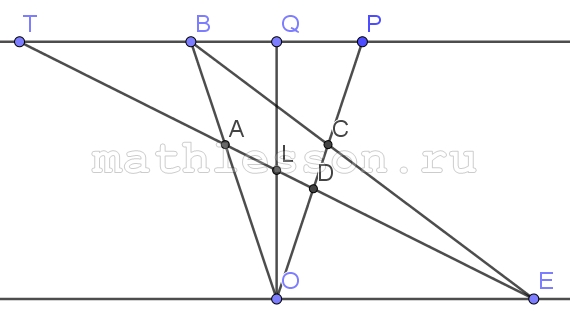
Б) 1) Пусть D располагается между O и C. Проведем через $$B n\left | \right |OM$$: $$OL\cap n=Q$$; $$OC\cap n=P$$; $$OA\cap n=T$$
2) Аналогично (A) $$\Delta OBP$$ – равнобедренный. Пусть $$AB=x\Rightarrow$$ $$OB=12+x$$ ; $$OP=PB=12+x=8+2+CP\Rightarrow$$ $$CP=x+2$$
3) $$\Delta BCP\sim \Delta COM$$: $$\frac{PB}{OM} =\frac{CP}{OC}\Rightarrow$$ $$BP=\frac{OM(x+2)}{10}$$; $$\Delta TPC\sim \Delta ODM$$: $$\frac{TP}{OM}=\frac{DP}{OD}\Rightarrow$$ $$TP=\frac{OM(x+4)}{8}$$; $$TB=TP-BP=OM(\frac{x+12}{40})$$; $$\Delta TBA\sim \Delta AOM$$: $$\frac{TB}{OM}=\frac{AB}{AO}\Rightarrow$$ $$\frac{x+12}{40}=\frac{x}{12}\Leftrightarrow$$ $$40x=12(x+12)\Leftrightarrow$$ $$x=\frac{36}{7}\Rightarrow$$ $$OB=12+\frac{36}{7}=\frac{120}{7}$$
4) Пусть $$S_{BOC}=S\Rightarrow$$ $$S_{AOD}=\frac{AO}{OB}*\frac{OD}{OC}S=$$$$\frac{12}{120}*\frac{8}{10}S=$$$$\frac{56}{100}S\Rightarrow$$ $$S_{ABCD}=S-\frac{56}{100}S=\frac{44}{100}S$$$$\Rightarrow$$ $$\frac{S_{AOD}}{S_{ABCD}}=$$$$\frac{56}{100}S:\frac{44}{100}S=\frac{14}{11}$$