ОГЭ математика 2019. Разбор варианта Алекса Ларина № 191.
Решаем ОГЭ 191 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №191 (alexlarin.com)
Решаем ОГЭ 191 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №191 (alexlarin.com)
Задание 1
Найдите значение выражения $$\frac{0,25}{0,3}(1,4-0,5*0,4)$$
$$\frac{0,25}{0,3}(1,4-0,5*0,4)=\frac{25}{30}*(1,4-0,2)=\frac{5}{6}*1,2=5*0,2=1$$
Задание 2
В таблице приведены расстояния от Солнца до четырех планет Солнечной системы. Какая из этих планет ближе всего к Солнцу
| Планета | Юпитер | Марс | Сатурн | Нептун |
| Расстояние (в км) | $$7,781*10^{8}$$ | $$2,280*10^{8}$$ | $$1,427*10^{9}$$ | $$4,497*10^{9}$$ |
Варианты ответа:
- Юпитер
- Марс
- Сатурн
- Нептун
У Сатурна и Нептуна степень 10 равна 9, следовательно, однозначно больше, чем у Юпитера и Марса. При этом 7,781 больше, чем 2,280. Тогда получаем, что расстояние до Марса наименьшее, что соответствует 2 варианту ответа
Задание 3
На координатной прямой отмечены числа x и y.
Какое из следующих утверждений об этих числах верно?
Варианты ответа
- x<y и |x|<|y|
- x>y и |x|>|y|
- x<y и |x|>|y|
- x>y и |x|<|y|
Как видим по рисунку $$x<0<y$$ и $$\left | x \right |<\left | y \right |$$. Тогда правильный ответ 1.
Задание 4
Значение какого из данных выражений является наименьшим?
- $$\sqrt{15}$$
- $$\frac{\sqrt{20}}{\sqrt{2}}$$
- $$2\sqrt{5}$$
- $$\sqrt{3}*\sqrt{6}$$
- $$\sqrt{15} = \sqrt{15}$$
- $$\frac{\sqrt{20}}{\sqrt{2}}=\sqrt{\frac{20}{2}}=\sqrt{10}$$
- $$2\sqrt{5}=\sqrt{2^2*5}=\sqrt{20}$$
- $$\sqrt{3}*\sqrt{6}=\sqrt{3*6}=\sqrt{18}$$
$$min= \sqrt{10}$$ или 2 вариант.
Задание 5
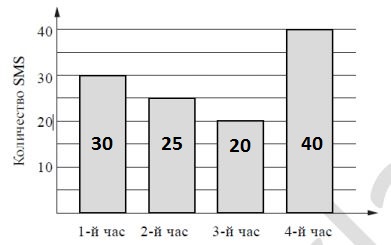
На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за последние два часа программы по сравнению с первыми двумя часами этой программы.
Как видим по диаграмме:
Задание 6
Решите уравнение $$4-\frac{3x-2}{7}=x$$
$$4-\frac{3x-2}{7}=x |*7$$ $$28-(3x-2)=7x$$ $$28-3x+2-7x=0$$ $$-10x=-30$$ $$x=3$$
Задание 7
Магазин покупает средство для стирки по 140 рублей за флакон и продает с наценкой 25%. Какое наибольшее число флаконов можно купить в этом магазине на 3000 рублей?
Раз наценка составляет 25%, то итоговая стоимость 125% 140 рублей -100% X рублей-125% $$x=\frac{140*125}{100}=175$$ рублей $$n=\frac{3000}{175}=17,14$$ флаконов. Т.е. 17 штук.
Задание 8
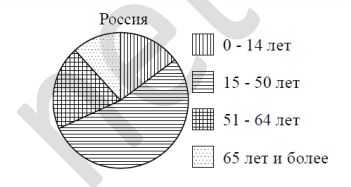
На диаграмме показан возрастной состав населения России. Определите по диаграмме, какая из возрастных категорий самая малочисленная.
Варианты ответа
- 0 – 14 лет
- 15 – 50 лет
- 51 – 64 лет
- 65 лет и более
Самый малочисленный сегмент соответствует возрасту 65 и более, что является 4 варианту ответа
Задание 9
На экзамене 25 билетов, Гриша не выучил 4 из них. Найдите вероятность того, что ему попадется выученный билет.
Выученных 25-4=2 билетов. Вероятность выученного : $$P=\frac{21}{25}=0,84$$
Задание 10
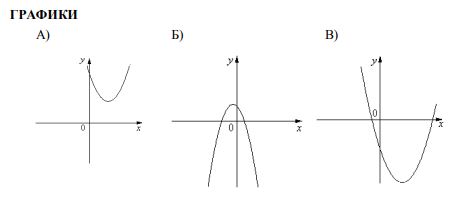
На рисунке изображены графики функций вида $$y=ax^{2}+bx+c$$ . Установите соответствие между графиками функций и знаками коэффициентов a и c.
КОЭФФИЦИЕНТЫ
- a>0, c<0
- a<0, c>0
- a>0, c>0
- a<0, c<0
Если a>0, то ветви вверх, если a<0, то вниз. Если c>0, то пересекает Oy график над Ox, если c<0, то под Ox. Тогда:
A :a>0; c>0 $$\Rightarrow$$ 3
Б :a<0; c>0 $$\Rightarrow$$ 2
B a:>0 ;c<0 $$\Rightarrow$$ 1
Задание 11
Последовательность $$a_{n}$$ задана условиями $$a_{1}=10, a_{n+1}=5-a_{n}$$. Найдите $$a_{11}$$
$$a_{1}=10, a_{n+1}=5-a_{n},a_{11}$$ -?
$$a_{2}=5-a_{1}=5-10=-5$$
$$a_{3}=5-a_{2}=5-(-5)=10$$
$$a_{4}=5-a_{3}=5-10=-5$$
Видим, что четные члены равны -5, а нечетные, начиная с третьего, равны 10. Тогда и 11ый член будет равен 10
Задание 12
Найдите значение выражения $$\frac{2}{5m}-\frac{5m+2n}{5mn}$$, при $$m=\sqrt{5}, n=\frac{2}{5}$$
$$\frac{2}{5m}-\frac{5m+2n}{5mn}=\frac{2n-5m-2n}{5mn}=$$$$\frac{-5m}{5mn}=-\frac{1}{n}=$$$$\frac{-1}{\frac{2}{5}}=-2,5$$
Задание 13
В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле $$C=150+11(t-5)$$, где t — длительность поездки, выраженная в минутах (t>5). Пользуясь этой формулой, рассчитайте стоимость 20-минутной поездки. Ответ укажите в рублях.
Найдем стоимость : $$C=150+11*(20-5)=$$$$150+11*15=150+165=315$$
Задание 14
Укажите неравенство, которое не имеет решений.
- $$x^{2}-25\leq 0$$
- $$x^{2}+25\geq 0$$
- $$x^{2}-25\geq 0$$
- $$x^{2}+25\leq 0$$
- $$x^{2}-25\leq 0\Leftrightarrow x \in [-5 ;5]$$
- $$x^{2}+25\geq 0\Leftrightarrow x \in R$$
- $$x^{2}-25\geq 0\Leftrightarrow x \in (-\infty ;-5]\cup [5; +\infty )$$
- $$x^{2}+25\leq 0\Leftrightarrow$$ решений нет
Задание 15
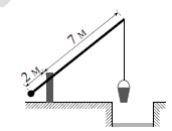
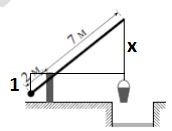
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
из подобия прямоугольных треугольников: $$\frac{2}{7}=\frac{1}{x}\Leftrightarrow x=\frac{7}{2}=3,5$$
Задание 16
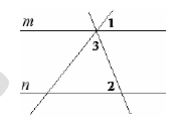
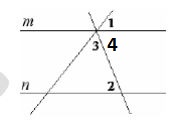
Прямые m и n параллельны. Найдите $$\angle 3$$, если $$\angle 1=58, \angle 2=62$$. Ответ дайте в градусах.
Задание 18
Боковая сторона равнобедренного треугольника равна 25, а основание равно 14. Найдите площадь этого треугольника.
Найдём полупериметр $$p=\frac{25+25+14}{2}=32$$ $$S=\sqrt{p(p-a)(p-b)(p-c)}=$$$$\sqrt{32(32-25)^{2}(32-14)}=$$$$\sqrt{2^{5}*7^{2}*2*3^{2}}=$$$$2^{3}*3*7=168$$
Задание 20
Какие из следующих утверждений верны?
- Площадь трапеции равна половине произведения основания трапеции на высоту
- Диагонали любого прямоугольника равны.
- Площадь ромба равна половине произведения его диагоналей.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
1)нет, полусумме оснований на высоту 2)верно 3)верно
Задание 21
Решите уравнение $$(x+3)(x^{2}-6x+9)=7(x-3)$$
Разложим на множители данное уравнение: $$(x+3)(x^{2}-6x+9)=7(x-3)$$ $$(x+3)(x^{2}-3)^{2}-7(x-3)=0$$ $$(x-3)((x+3)(x-3)-7)=0$$ Произведение равно нулю, когда хотя бы один из множителей равен нулю: $$\left\{\begin{matrix}x-3=0 \\x^{2}-9-7=0 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=3 \\x^{2}=16 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=3 \\x=4 & & & \\x=-4 \end{matrix}\right.$$
Задание 22
Из пункта А в пункт В выехал грузовик. Через час из пункта А выехал легковой автомобиль. Через 2 часа после выезда он догнал грузовик и прибыл в пункт В на 3 часа раньше грузовика. Сколько времени грузовик ехал от А до В?
Пусть x-скорость авто,y-скорость грузовика, 1-расстояние от A до B. Тогда : Раз выехал через час, и догнал через 2, то грузовик ехал 3 часа и автомобиль 2 часа. Тогда пройденное расстояние у них одинаково: $$3y=2x(1)$$ Раз приехал на 3 часа раньше , то в пути был на 3+1=4 часа меньше и время автомобиля на 4 часа меньше, чем времени грузовика: $$\frac{1}{y}-\frac{1}{x}=4(2)$$ Из (1): $$x=\frac{3y}{2}$$ подставим в (2): $$\frac{1}{y}-\frac{2}{3y}=4\Leftrightarrow$$ $$\frac{3-2}{3y}-4\Leftrightarrow 3y=\frac{1}{4}\Leftrightarrow$$ $$y=\frac{1}{12}$$ Тогда время грузовика: $$\frac{1}{\frac{1}{12}}=12$$ часов
Задание 23
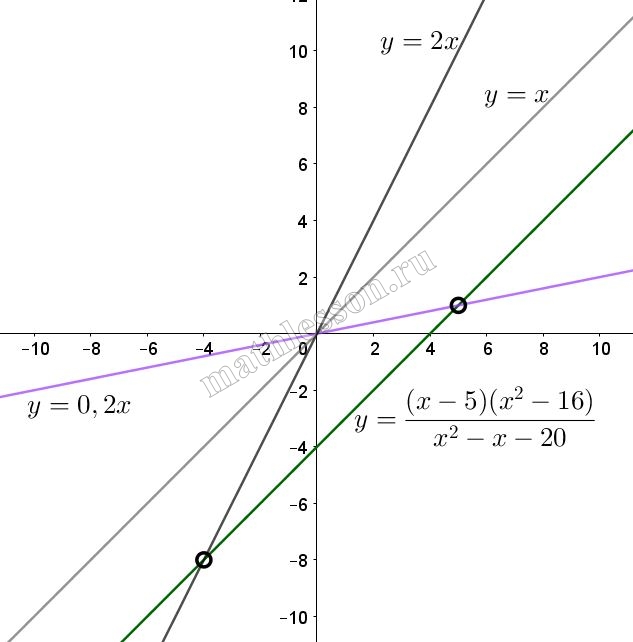
Постройте график функции $$y=\frac{(x-5)(x^{2}-16)}{x^{2}-x-20}$$ и определите, при каких значениях k построенный график не будет иметь общих точек с прямой $$y=kx$$ .
$$y=\frac{(x-5)(x^{2}-16)}{x^{2}-x-20}$$
Найдем область определения. Так как есть знаменатель, то он не равен нулю:
$$x^{2}-x-20\neq 0$$
$$\left\{\begin{matrix}x_{1}+x_{2}\neq 1 \\x_{1}*x_{2}\neq -20 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}\neq -4 \\x_{2}=5 \end{matrix}\right.$$
Воспользуемся формулой: $$ax^{2}+bx+c=a(x-x_{1})(x-x_{2})$$:
$$y=\frac{(x-5)(x-4)(x+4)}{(x+4)(x-5)}=x-4$$
Не будет иметь если $$y=kx$$ пройдет через точку (5;1) или (-4;-8), а так же если будет параллельна:
1)$$1=5*k\Rightarrow k=0,2$$
2) $$-8=(-4)k\Rightarrow k=2$$
3) Прямые параллельны, если их коэффициенты при х равны. То есть прямая $$y=kx$$ параллельна $$y=x-4$$ при $$k=1$$
Задание 24
В треугольник со сторонами АВ=8, ВС=6, АС=4 вписана окружность. Найдите длину отрезка DE, где D, Е – точки касания этой окружности со сторонами АВ и АС соответственно.
1) Пусть O-центр окружности , тогда: $$OD\perp AB OE\perp AC$$ (свойство радиуса к касательной)
2) $$OD=OC=\frac{S}{p}=$$$$\sqrt{\frac{(p-a)(p-b)(p-c)}{p}}$$ (формула Герона); $$p=\frac{8+6+4}{2}=9$$; $$OD=\sqrt{\frac{(9-6)(9-8)(9-4)}{9}}=$$$$\sqrt{\frac{3*1*5}{9}}=\sqrt{\frac{5}{3}}$$
3) $$\cos A=\frac{AB^{2}+AC^{2}-BC^{2}}{2*AB*AC}=\frac{8^{2}+4^{2}-6^{2}}{2*8*4}=\frac{11}{16}$$ (теорема косинусов)
4) $$\angle DOE=180-\angle A\Rightarrow$$ $$\cos DOE=-\cos A=-\frac{11}{16}$$
5)$$\Delta DOE$$: $$DE=\sqrt{DO^{2}+OE^{2}-2DO*OE*\cos DOE}=$$$$\sqrt{\frac{5}{3}+\frac{5}{3}+2\frac{5}{3}*\frac{11}{16}}=$$$$\sqrt{\frac{10}{36}+\frac{110}{16*3}}=$$$$\sqrt{\frac{270}{16*3}}=\sqrt{\frac{90}{16}}=\frac{3\sqrt{10}}{4}$$
Задание 25
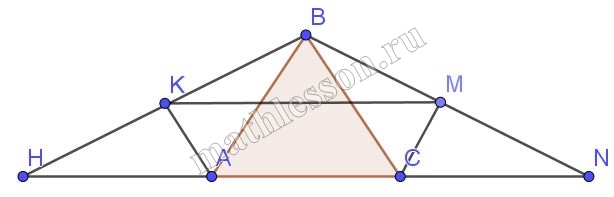
Из вершины В треугольника АВС опущены перпендикуляры ВК и ВМ на биссектрисы внешних углов треугольника, не смежных с углом В. Докажите, что длина отрезка КМ равна полупериметру треугольника АВС.
1) $$BK\cap AC=H; BM\cap AC=N$$
Из $$\Delta HAB$$: AK-высота и биссектриса $$\Rightarrow$$ и медиана и $$AH=AB$$ ($$\Delta AHB$$-равнобедренный)
Из $$\Delta BCH$$: аналогично CM-медиана и BC=CN
2) из п. 1 $$HN=HA+AC+CN=$$$$AB+AC+DC=P_{ABC}$$
K и M-середины , тогда KM-средняя линия и $$KM=\frac{1}{2}HN=\frac{P_{ABC}}{2}$$
Задание 26
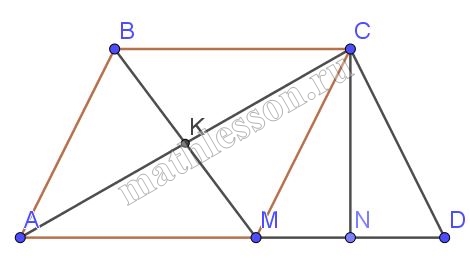
В равнобедренной трапеции АВСD углы при основании АD равны 30, диагональ АС является биссектрисой угла ВАD. Биссектриса угла ВСD пересекает основание АD в точке М, а отрезок ВМ пересекает диагональ АС в точке К. Найдите площадь треугольника АКМ, если площадь трапеции АВСD равна $$2+\sqrt{3}$$ см2 .
1) Пусть $$AB=CD=a$$, $$\angle BAC=\angle CAD$$(AC-биссектриса ), $$\angle CAD=\angle ACB$$(накрест лежащие),тогда $$\angle BAC=\angle BCA\Rightarrow$$ $$AB=BC=a$$
2) Аналогично для $$\Delta CMD$$ : $$\angle BCM=\angle CMD$$, $$\angle BCM=\angle MCD$$, тогда $$\angle CMD=\angle MCD$$ и $$CD=MD=a$$
3) из п.2 и параллельности BC и MD получим, что BCDM-параллелограмм; $$BM=CD=a$$, $$\Delta A_{1}BM$$ -равнобедренный; $$\angle ABM=180-2*30=120$$
По теореме косинусов : $$AM=\sqrt{AB^{2}+BM^{2}-2AB*BM*\cos ABM}=$$$$\sqrt{a^{2}+a^{2}-2*a*a*\cos 120}=a\sqrt{3}$$
4) AK-биссектриса , тогда $$\frac{AB}{AM}=\frac{AK}{KM}=$$$$\frac{a}{\sqrt{30}}=\frac{1}{\sqrt{3}}$$, тогда $$\frac{KM}{BM}=\frac{\sqrt{3}}{\sqrt{3}+1}$$ и $$S_{\Delta AKM}=\frac{\sqrt{3}}{\sqrt{3}+1}S_{ABM}$$
5) Пусть $$CN\perp AD$$,тогда из $$\Delta CND$$: $$CH=CD*\sin D=\frac{a}{2}$$
6) $$S_{ABD}=\frac{a+a+a\sqrt{3}}{2}*\frac{a}{2}=$$$$\frac{a^{2}}{4}(2+\sqrt{3})=2+\sqrt{3}\Rightarrow$$ $$a^{2}=4\Rightarrow a=2$$
7)$$S_{ABM}=\frac{1}{2}*a*a* \sin 120=$$$$\frac{\sqrt{3}a^{2}}{4}=\sqrt{3}$$
$$S_{AKM}=\frac{\sqrt{3}}{\sqrt{3}+1}*\sqrt{3}=$$$$\frac{3}{\sqrt{3}+1}$$