ОГЭ математика 2018. Разбор варианта Алекса Ларина № 184.
Решаем ОГЭ 184 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №184 (alexlarin.com)
Решаем ОГЭ 184 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №184 (alexlarin.com)
Задание 1
В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
| Вещество | Дети от 1 года до 14 лет | Мужчины | Женщины |
| Жиры | 40-97 | 70-154 | 60-102 |
| Белки | 36-87 | 65-117 | 58-87 |
| Углеводы | 170-420 | 257-586 | 257-586 |
Следовательно, ответом будет 13
Задание 2
Модуль - это расстояние от начала координат до числа, как видим по рисунку, расстояние оу больше, чем ох, следовательно: |x|<|y|. С другой стороны число х левее, чем число у, следовательно, x
Задание 3
Найдите значение выражения $$\sqrt{0,48}*\frac{1}{\sqrt{12}}$$ Варианты ответа 1)0,6 2)$$\sqrt{3}$$ 3)0,2 4)$$\frac{\sqrt{3}}{4}$$
$$\sqrt{0,48}*\frac{1}{\sqrt{12}}=$$$$\sqrt{\frac{48}{100*12}}=$$$$\sqrt{\frac{4}{100}}=\frac{2}{10}=0,2$$. Что соответствует 3 варианту ответа
Задание 4
На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря. Определите по графику, на сколько градусов Цельсия температура на высоте 250 метров выше, чем на высоте 650 метров.
250 метров - 9 градусов, 650 метров - 7 градусов. Тогда разница составит : 9-7=2
Задание 5
Решите уравнение $$5-\frac{2x-7}{4}=-5x$$
$$5-\frac{2x-7}{4}=-5x\Leftrightarrow $$$$20-2x+7=-20x\Leftrightarrow $$$$-2x+20x=-20-7\Leftrightarrow $$$$18x=-27|:18\Leftrightarrow x=-1,5$$
Задание 6
В городе 90000 жителей, причём 32% — это пенсионеры. Сколько примерно человек составляет эта категория жителей? Ответ округлите до тысяч.
Пусть х - количество пенсионеров, тогда : 90000 - 100% x - 32% Тогда: $$x=\frac{90000*32}{100}=28800$$ человек. Тогда вы тысячах человек это будет примерно 29.
Задание 7
На диаграмме показан возрастной состав населения России. Определите по диаграмме, какая из возрастных категорий самая малочисленная.
Наименьший сегмент составляет возрастная группа 65 лет и более, что соответствует 4 варианту ответа.
Задание 8
На экзамене 60 билетов, Василий не выучил 12 из них. Найдите вероятность того, что ему попадется выученный билет.
Вероятность того, что попадется не выученный: $$P=\frac{12}{60}=0,2$$. Тогда вероятность противоположного события (выученный) будет равна: $$1-P=1-0,2=0,8$$
Задание 9
На рисунке изображены графики функций вида $$y=ax^{2}+bx+c$$ . Установите соответствие между графиками функций и знаками коэффициентов a и c.
КОЭФФИЦИЕНТЫ
1) a>0, c>0
2)a<0, c>0
3) a>0, c>0
Коэффициент а отвечает за направление ветвей параболы, если а > 0, то ветви вверх, если а < 0, то ветви вниз. Коэффициент с показывает ординату точки пересечения графиком оси оУ, если с > 0, то пересекает над осью оХ, если c < 0, то под осью оХ. Тогда получаем:
Задание 10
Последовательность $$a_{n}$$ задана условиями $$a_{1}=-3, a_{n+1}=a_{n}-3$$. Найдите $$a_{21}$$
Найдем разность арифметической прогрессии: $$d=a_{n+1}-a_{n}=a_{n}-3-a_{n}=-3$$. Найдем 21 член прогрессии: $$a_{n}=a_{1}+d(n-1)$$ Тогда $$a_{21}=-3-3*(21-1)=-63$$
Задание 11
Найдите значение выражения $$\frac{1}{a}-\frac{3a+b}{ab}$$, при $$a=\sqrt{5} ; b = \frac{1}{5}$$
$$\frac{1}{a}-\frac{3a+b}{ab}=$$$$\frac{b-3a-b}{ab}=$$$$-\frac{3a}{ab}=$$$$-\frac{3}{b}=$$$$-\frac{3}{\frac{1}{5}}=-15$$
Задание 12
В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле $$C=150+11\cdot(t-5)$$, где t — длительность поездки, выраженная в минутах (t>5). Пользуясь этой формулой, рассчитайте стоимость 24-минутной поездки. Ответ укажите в рублях.
$$C=150+11\cdot(24-5)=359$$
Задание 13
Укажите неравенство, которое не имеет решений
1)$$x^{2}-169\geq 0$$
2)$$x^{2}+169\geq 0$$
3)$$x^{2}-169\leq0$$
4)$$x^{2}+169\leq0$$
Если можно найти какой-либо корень уравнения в данном случае, то неравенства будут иметь решения, то есть $$x^{2}-169=0 \Leftrightarrow$$$$x=\pm 13$$. Следовательно, оба неравенства, где слева стоит данное выражения будут иметь решения. $$x^{2}+169$$ всегда принимает положительные значения, так как это сумма неотрицательного и положительного. Следовательно, $$x^{2}+169\geq 0$$ - имеет решением любое число, тогда $$x^{2}+169\leq0$$ вообще не имеет решений
Задание 14
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
Пусть х - расстояние от человека до фонаря, тогда из подобия треугольников ABC и A1B1C: $$\frac{AB}{A_{1}B_{1}}=\frac{BC}{B_{1}C} \Leftrightarrow$$ $$\frac{4}{1,8}=\frac{x+9}{9} |*9 \Leftrightarrow$$$$\frac{4}{0,2}=x+9 \Leftrightarrow$$$$x=20-9=11$$
Задание 15
Прямые m и n параллельны. Найдите $$\angle 1$$, если $$\angle 2 = 52^{\circ}, \angle 3 = 48^{\circ}$$. Ответ дайте в градусах.
Угол 2 равен углу 4 как накрестлежащие, но сумма углов 3,4,1 равна 180, тогда $$\angle 1=180 - 52 - 48 = 80$$
Задание 16
Основания трапеции равны 5 и 14. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
В треугольнике ABD HM - средняя линия, тогда: $$HM = \frac{1}{2}AB=2,5$$
В треугольнике BDC ML - средняя линия, тогда: $$ML=\frac{1}{2}DC=7$$
Задание 17
Боковая сторона равнобедренного треугольника равна 26, а основание равно 10. Найдите площадь этого треугольника.
Высота треугольника : $$h = \sqrt{26^{2}-5^{2}}=\sqrt{651}$$. Тогда его площадь $$S=\frac{1}{2}h*10=5\sqrt{651}$$
Задание 18
В треугольнике ABC угол C равен 90°, СН – высота, AВ = 16, sin A = 3/4 . Найдите BН
Из треугольника ABC : $$CB=AB\sin A = 16*\frac{3}{4}=12$$. $$\angle A = \angle HCB$$ из подобия треугольников при проведении высоты в прямоугольном треугольнике. Из треугольника CHB: $$HB=CB \sin HCB = 12* \frac{3}{4}=9$$
Задание 19
Какие из следующих утверждений верны?
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
1) Неверно, так как это трапеция 2) Верно 3) Верно
Задание 20
Решите уравнение $$(x+2)(x^{2}-6x+9)=-4(x-3)$$
$$(x+2)(x^{2}-6x+9)=-4(x-3) \Leftrightarrow$$$$(x+2)(x^-3)^{2}+4(x-3)=0 \Leftrightarrow$$$$(x-3)((x+2)(x-3)+4)=0$$ Произведение равно нулю, когда один из множителей равен нулю: $$\left [ \begin{matrix}x-3=0\\ (x+2)(x-3)+4=0\end{matrix}\right.\Leftrightarrow $$$$\left [ \begin{matrix}x=3\\ x^{2}-x-2=0\end{matrix}\right.\Leftrightarrow $$$$\left [ \begin{matrix}x=3\\ x=2\\ x=-1\end{matrix}\right.$$
Задание 21
Двое рабочих могут вместе выполнить 2/3 некоторой работы за 4 дня. За сколько дней каждый рабочий может выполнить всю работу, если один из них может сделать это на 5 дней раньше, чем второй.
Пусть х - производительность первого в день, y - производительность второго в день. Объем всей работы равен 1. Тогда: $$x+y=\frac{\frac{2}{3}}{4}=\frac{1}{6}$$ (объем работы поделили на количество дней и получили суммарную производительность). Отсюда $$x=\frac{1-6y}{6}$$. Пусть первый работает медленнее, тогда $$\frac{1}{x}-\frac{1}{y}=5$$. Подставим в это уравнение выраженное значение х через у: $$\frac{1}{\frac{1-6y}{6}}-\frac{1}{y}=5 \Leftrightarrow$$$$\frac{6}{1-6y}-\frac{1}{y}=5\Leftrightarrow$$$$6y-1+6y=5y-30y^{2}\Leftrightarrow$$$$30y^{2}+7y-1=0$$. Отсюда $$y_{1}=\frac{1}{10}$$ ; $$y_{2}$$ меньше нуля. Следовательно, время второго $$t=\frac{1}{\frac{1}{10}}=10$$, тогда время первого на пять дней больше, то есть 15
Задание 22
Постройте график функции $$y=\frac{(x-4)(x^{2}-4)}{x^{2}-6x+8}$$ и определите, при каких значениях k построенный график не будет иметь общих точек с прямой у=kx
Найдем область определения заданной функции: $$x^{2}-6x+8 \neq 0 \Leftrightarrow $$$$x_{1} \neq 2 ; 4$$
Преобразуем данную функцию с учетом полученной области определения: $$\frac{(x-4)(x^{2}-4)}{x^{2}-6x+8}=$$$$\frac{(x-4)(x-2)(x+2)}{(x-4)(x-2)}=x+2$$. То есть график функции $$y=x+2$$ совпадает с графиком начальной функции при наличии области ее определения.
Получаем, что точки (2;4) и (4;6) пустые, следовательно, чтобы прямая y=kx не имела с графиком пересечений, она должна пройти через эти точки. Подставим их координаты в уравнение прямой, чтобы найти k:
$$4=2k \Leftrightarrow$$$$k=2$$
$$6=4k \Leftrightarrow$$$$k=1,5$$
Так же прямая не будет иметь пересечений, если она будет параллельна графику начальной функции. Две прямые $$y_{1}=k_{1}x+b_{1}$$ и $$y_{2}=k_{2}x+b_{2}$$ параллельны в том случае, если коэффициенты при х у них одинаковы ($$k_{1}=k_{2}$$, а свободные - разные ($$b_{1} \neq b_{2}$$). То есть k=1 тоже будет ответом.
Задание 23
Найдите площадь прямоугольного треугольника, если биссектриса прямого угла делит гипотенузу на отрезки длины 15 и 20 см.
1)$$\frac{AC}{CB}=\frac{AL}{LB}=\frac{3}{4}$$ по свойству биссектрисы. Тогда, пусть AC=3x ; CB=4x
2)Из треугольника ABC по теореме Пифагора: $$AC^{2}+CB^{2}=AB^{2} \Leftrightarrow$$$$(3x)^{2}+(4x)^{2}=35^{2}$$. Отсюда x=7. Тогда AC=21 ; CB = 28.
3)$$S_{ABC}=\frac{1}{2}AC*CB=\frac{1}{2}*21*28=294$$
Задание 24
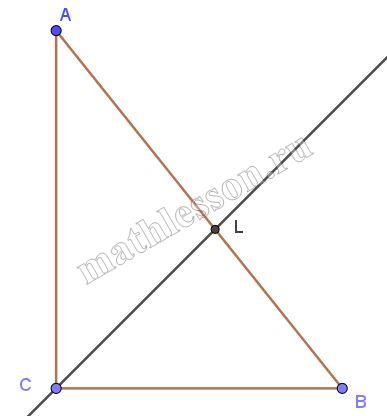
На стороне $$BC$$ квадрата $$ABCD$$ взята точка $$M$$. Докажите, что площадь треугольника $$AMD$$ равна половине площади квадрата.
1)Пусть $$MH \perp AD$$ , тогда ABMH - прямоугольник и MH=AB
2)$$S_{AMD}=\frac{1}{2}AD*MH$$, или $$S_{AMD}=\frac{1}{2}AD*AB=\frac{1}{2}S_{ABCD}$$
Задание 25
Диагонали вписанного в окружность четырехугольника $$ABCD$$ пересекаются в точке $$E$$, причем $$AD\cdot CE=DC\cdot AE$$, $$BD=6$$, $$\angle ADB=22,5^{\circ}$$. Найдите площадь четырехугольника $$ABCD$$.
1) AD*CE=CD*AE, тогда $$\frac{AD}{CD}=\frac{AE}{CE} \Leftrightarrow$$ DB - биссектриса в треугольнике ADC. Тогда $$\angle BDA = \angle CDB$$ , но $$\angle BDA = \angle BCA$$ и $$\angle CDB = \angle BAC$$ (как вписанные), следовательно $$\angle BCA = angle BAC$$ , тогда треугольник ABC - равнобедренный
2)Построим продолжение DС за точка C и отложим из B отрезок BF = DB так, что $$F \in DC$$. Тогда треугольник DBF - равнобедренный. Так как AB = BC, DB = BF и из равнобедренности DBF $$\angle BDF = \angle BFD$$, но и $$\angle BDA = \angle CDB$$, тогда $$\angle BDA=\angle BFD$$. $$\angle BAD + \angle DCB = 180$$ по свойству вписанного четырехугольника, но и $$\angle BCF + \angle DCB = 180$$ по свойству смежных углов, тогда $$\angle BAD = \angle BCF$$ и, следовательно, треугольники ABD и BCF равны, следовательно, $$S_{ADF}=S_{ABCD}$$
3)$$\angle DBF = 180 - 2*22.5 = 135$$ (из треугольника DBF), $$S_{DBF}=\frac{1}{2}DB*DF*\sin DBF$$, то есть $$S_{DBF}=0,5*6*6*\frac{\sqrt{2}}{2}=9\sqrt{2}$$