ОГЭ математика 2019. Разбор варианта Алекса Ларина № 197.
Решаем ОГЭ 197 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №197 (alexlarin.com)
Решаем ОГЭ 197 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №197 (alexlarin.com)
Задание 1
Найдите значение выражения $$10*5^{-3}+8*5^{-2}+6*5^{-1}$$
$$10*5^{-3}+8*5^{-2}+6*5^{-1}=$$$$5^{-1}(10*5^{-2}+8*5^{-1}+6)=$$$$\frac{1}{5}(\frac{10}{25}+\frac{8}{5}+\frac{6}{1})=$$$$\frac{1}{5}(\frac{2}{5}+\frac{8}{5}+6)=$$$$\frac{1}{5}(2+6)=\frac{8}{5}=1,6$$
Задание 2
В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
| Вещество | Дети от 1 года до 14 лет | Мужчины | Женщины |
| Жиры | 40–97 | 70–154 | 60–102 |
| Белки | 36–87 | 65–117 | 58–87 |
| Углеводы | 170–420 | 257–586 | 257–586 |
Какой вывод о суточном потреблении жиров, белков и углеводов женщиной можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 50 г жиров, 60 г белков и 250 г углеводов? В ответе укажите номера верных утверждений.
- Потребление жиров в норме.
- Потребление белков в норме.
- Потребление углеводов в норме.
- Потребление жиров в норме - неверно, так как 50 меньше 60
- Потребление белков в норме - верно
- Потребление углеводов в норме - неверно, так как 250 меньше 257
Задание 3
Одно из чисел, $$\sqrt{2},\sqrt{3},\sqrt{5},\sqrt{8}$$ отмечено на прямой, точкой А. Какое это число?
Варианты ответа
- $$\sqrt{2}$$
- $$\sqrt{3}$$
- $$\sqrt{5}$$
- $$\sqrt{8}$$
Число A $$\in (2,3)\Rightarrow$$ $$A \in (\sqrt{4}, \sqrt{9})$$. Число ближе к 2 $$\Rightarrow$$ $$A=\sqrt{5}$$, что соответствует 3 варианту ответа
Задание 4
Найдите значение выражения $$5\sqrt{2}*\sqrt{22}*3\sqrt{11}$$
$$5\sqrt{2}*\sqrt{22}*3\sqrt{11}=$$$$15\sqrt{22*22}=15*22=330$$
Задание 5
Когда самолёт находится в горизонтальном полёте, подъёмная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолёта. На оси абсцисс откладывается скорость (в км/ч), на оси ординат — сила (в тоннах силы). Определите по рисунку, чему равна подъёмная сила (в тоннах силы) при скорости 400 км/ч
При скорости в 400 км/ч сила составит 4 тс
Задание 6
Решите уравнение $$\frac{1-3x}{4}=\frac{5x}{8}+6,5$$
$$\frac{1-3x}{4}=\frac{5x}{8}+6,5|*8$$ $$2(1-3x)=5x+52$$ $$2-6x-5x=52\Leftrightarrow$$ $$-11x=50\Leftrightarrow$$ $$x=-\frac{50}{11}$$
Задание 7
Спортивный магазин проводит акцию. Любая футболка стоит 300 рублей. При покупке двух футболок — скидка на вторую футболку 70%. Сколько рублей придётся заплатить за покупку двух футболок в период действия акции?
Стоимость второй футболки с учетом скидки :300*0,3=90 Тогда итоговая стоимость двух футболок: 300+90=390
Задание 8
На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира. Какие из следующих утверждений верны?
- Индонезия входит в семёрку крупнейших по площади территории стран мира
- Площадь территории США составляет 8,5 млн км2.
- Площадь Австралии больше площади Индии.
- Площадь Канады больше площади Индии более чем в три раза.
- Индонезия входит в семёрку крупнейших по площади территории стран мира - неверно, Индонезии нет среди стран
- Площадь территории США составляет 8,5 млн км2 - неверно, 9,5
- Площадь Австралии больше площади Индии - верно
- Площадь Канады больше площади Индии более чем в три раза - верно
Задание 9
На полку в случайном порядке поставили три учебника: по истории, литературе и географии. Найдите вероятность того, что учебники по литературе и географии стоят рядом. Результат округлите до сотых.
И-история, Л-литература , Г-география: Все возможные расположения : ИЛГ; ИГЛ; ГИЛ; ГЛИ; ЛГИ; ЛИГ. Л и Г рядом в 4 из 6 случаев. Тогда : $$P=\frac{4}{6}\approx 0,67$$
Задание 10
График какой из приведенных ниже функций изображён на рисунке?
Варианты ответа
- $$y=x^{2}-2$$
- $$y=-x^{2}+2$$
- $$y=x^{2}+4$$
- $$y=-x^{2}+4$$
Ветви вниз $$\Rightarrow a<0$$. Пресекает Oy при y=4 $$\Rightarrow$$ c=4. Тогда $$y=-x^{2}+4$$, что соответствует 4 варианту ответа
Задание 11
Выписаны первые несколько членов арифметической прогрессии: 15; 30; 45; ... Найдите сумму первых тринадцати её членов.
Найдем разность прогрессии: $$d=a_{n}-a_{n+1}=30-15=15$$. Найдём сумму первых тридцати (n=13): $$S_{n}=\frac{2a_{1}+d(n-1)}{2}*n=$$$$\frac{2*15+15(13-1)}{2}*13=1365$$
Задание 12
Найдите значение выражения $$(\frac{a+3b}{a^{2}-3ab}-\frac{1}{a}):\frac{b}{3a-b}$$, при $$a=-5\frac{1}{3}$$, $$b=-5$$
$$(\frac{a+3b}{a^{2}-3ab}-\frac{1}{a}):\frac{b}{3a-b}=$$$$\frac{a+3b-(a-3b)}{a(a-3b)}*\frac{(3a-b)}{b}=$$$$\frac{6b*(-1)}{ab}=\frac{-6}{a}=$$$$-6:(-5\frac{1}{3})=$$$$\frac{6*3}{16}=\frac{9}{8}=1,125$$
Задание 13
Площадь четырёхугольника можно вычислить по формуле $$S=\frac{d_{1}d_{2}\sin \alpha}{2}$$, $$d_{1},d_{2}$$ - длины диагоналей четырёхугольника, $$\alpha$$ - угол между диагоналями. Пользуясь этой формулой найдите длину диагонали $$d_{2}$$, если $$d_{1}=6, \sin \alpha=\frac{1}{3}, S=19$$
$$d_{2}=\frac{2S}{d_{1}\sin \alpha }=$$$$\frac{2*19}{6*\frac{1}{3}}=19$$
Задание 14
$$x^{2}-5x-6\leq 0\Leftrightarrow$$ $$(x-6)(x+1)\leq 0\Leftrightarrow$$$$x \in [-1;6]$$, что соответствует 4 варианту ответа
Задание 15
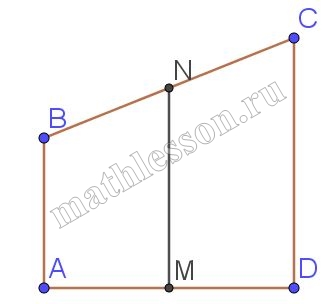
Наклонная балка поддерживается тремя столбами, стоящими вертикально на равном расстоянии друг от друга. Длины двух меньших столбов — 50 см и 70 см. Найдите длину большего столба. Ответ дайте в см.
ABCD -трапеция, MN-средняя линия: $$\frac{50+x}{2}=70\Leftrightarrow$$ $$50+x=140\Leftrightarrow$$ $$x=90$$
Задание 16
В треугольнике ABC проведена биссектриса AМ, угол AМC равен 130, угол ABC равен 110. Найдите угол ACB. Ответ дайте в градусах.
$$\angle AMB=180-\angle AMC=50$$
$$\Delta ABM$$: $$\angle BAM=180-(110+50)=20\Rightarrow$$ $$\angle A=20*2=40$$
$$\angle ACB=180-(110+40)=30$$
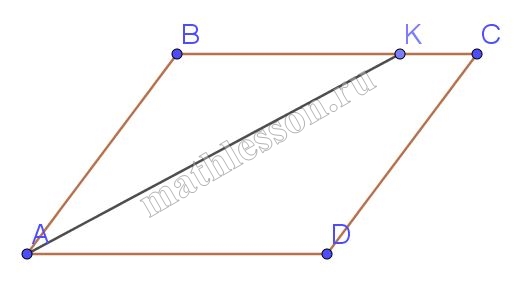
Задание 17
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=10, CK=18.
BC=10+18=28 $$\angle BAK=\angle KAD$$(AK-биссектриса )
$$\angle BKA=\angle KAD$$ (накрест лежащие)$$\Rightarrow \angle BAK=\angle BKA\Rightarrow$$
$$AB=BK=10$$ $$P=(10+28)*2=76$$
Задание 18
Высота равностороннего треугольника равна $$\sqrt{12}$$. Найдите его периметр.
Найдем сторону треугольника: $$AB=\frac{BH}{\sin A}=$$$$\frac{\sqrt{12}}{\sin 60}=$$$$\frac{\sqrt{12}*2}{\sqrt{3}}=4$$
Найдем периметр треугольника: $$P=4*3=12$$
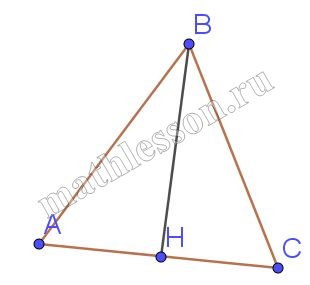
Задание 19
В треугольнике ABC угол C равен 90, CH — высота, BC=15, CH=9. Найдите sin A
$$\sin A=\sin HCB$$( из $$\Delta ABC\sim \Delta HCB$$)
$$\sin HCB=\frac{HB}{CB}$$
$$HB=\sqrt{15^{2}-9^{2}}=12$$
$$\sin HCB=\frac{12}{15}=0,8$$
Задание 20
Какие из следующих утверждений верны?
- Если угол острый, то вертикальный ему угол также является острым.
- Диагонали ромба взаимно перпендикулярны.
- В плоскости все точки, равноудалённые от заданной точки, лежат на одной прямой.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
- Если угол острый, то вертикальный ему угол также является острым - верно
- Диагонали ромба взаимно перпендикулярны - верно
- В плоскости все точки, равноудалённые от заданной точки, лежат на одной прямой - неверно, на окружности
Задание 21
Решите систему уравнений: $$\left\{\begin{matrix}x^{2}-xy+y^{2}=79\\ x-y=7\end{matrix}\right.$$
$$\left\{\begin{matrix}x^{2}-xy+y^{2}=79\\x-y=7\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}(7+y)^{2}-(7+y)y+y^{2}=79\\x=7+y\end{matrix}\right.$$
$$49+14y+y^{2}-7y-y^{2}+y^{2}-79=0\Leftrightarrow$$$$y^{2}+7y-30=0$$
$$\left\{\begin{matrix}y_{1}+y_{2}=-7\\y_{1}y_{2}=-30\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}y_{1}=-10\\y_{2}=3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=7-10=-3\\x_{2}=7+3-10\end{matrix}\right.$$
Задание 22
Два насоса, работая одновременно, заполняют бак за 3 часа 12 минут. Первый насос заполнил часть объёма бака, проработав 2 часа, а затем оставшуюся часть на 800л большую заполнил второй насос, проработав 4 часа. Каков объём бака?
Пусть x-производительность первого (л\г), y-второго, V-объем. Тогда :
$$\frac{V}{x+y}=3\frac{12}{60}$$ - работали вместе
$$4y-2x=800$$ - разность в 800 метров
$$2x+4y=V$$ - заполнили за 2 и 4
$$\left\{\begin{matrix}\frac{V}{x+y}=3\frac{1}{5}=\frac{16}{5}\\4y-2x=800\\4y+2x=V\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}5V=16(x+y)\\8y=V+800\\2x=4y-800\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}5V=16x+16y\\8y=V+800\\4x=V+800-1600\end{matrix}\right. \Leftrightarrow$$ $$\left\{\begin{matrix}5V=16x+16y\\8y=V+800\\4x=V-800\end{matrix}\right.$$
$$5V=4(V-800)+2(V+800)\Leftrightarrow$$ $$5V=4V-3200+2V+1600\Leftrightarrow$$ $$1600=V$$
Задание 23
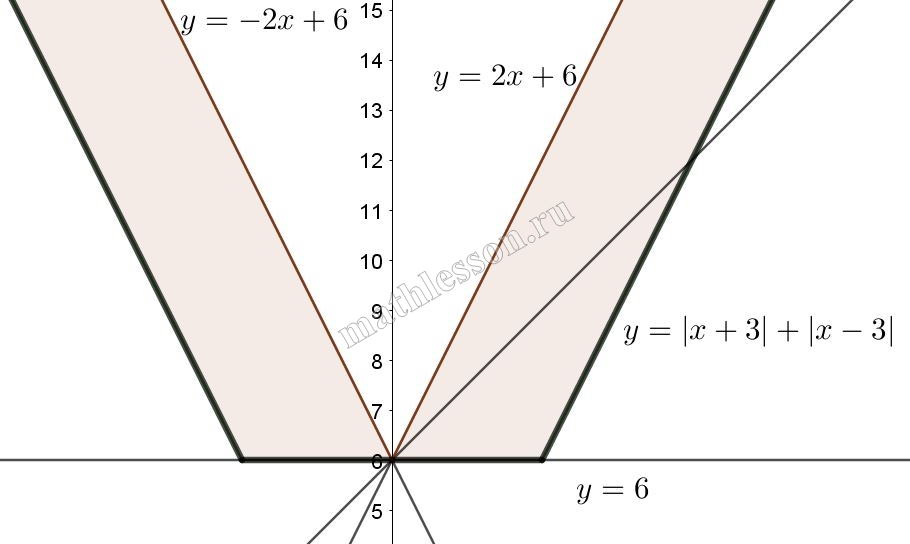
Постройте график функции $$y=|x+3|+|x-3|$$ и найдите все значения а, при которых прямая $$y=ax+6$$ имеет с графиком ровно две общие точки.
Раскроем модуль:
$$x\leq -3\Leftrightarrow y=-x-3-x+3=-2x$$
$$x \in (-3, 3]\Leftrightarrow y=x+3-x+3=6$$
$$x>3\Rightarrow y=x+3+x-3=2x$$
Начертим график:
Видим, что две точки пересечения будут в том случае, если прямая лежит в первой четверти при $$a\in(0;2)$$ (от момента, когда она будет параллельна оси Ох, до момента, когда она будет параллельна прямой $$y=2x$$) и, если прямая лежит во второй четверти при $$a\in(-2;0)$$ (от момента, когда она будет параллельна $$y=-2x$$, до момента, когда она будет параллельна оси Ох): $$a \in (-2;0)\cup (0;2)$$
Задание 24
Площадь равнобедренного треугольника с острым углом при вершине равна 48, а боковая сторона равна 10. Найдите высоту, опущенную на основание.
1) $$S=\frac{1}{2}AB*BC *\sin B\Rightarrow$$ $$\sin B=\frac{2S}{AB^{2}}=$$$$\frac{2*48}{100}=0,96\Rightarrow$$ $$\cos B=\sqrt{1-0,96^{2}}=0,28$$
2) $$AC=\sqrt{AB^{2}+BC^{2}-2AB*BC\cos B}=$$$$\sqrt{10^{2}+10^{2}-2*10*10*0,28}=12$$$$\Rightarrow HC=6$$
3) из $$\Delta BHC$$: $$BH=\sqrt{BC^{2}-HC^{2}}=\sqrt{10^{2}-6^{2}}=8$$
Задание 25
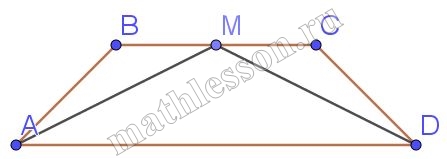
Биссектрисы углов А и D равнобедренной трапеции АВСD пересекаются в точке М стороны ВС. Докажите, что М – середина ВС.
1) $$\angle A=\angle D\Rightarrow$$ $$\angle BAM=\angle MDC$$
2) $$\angle BAM=\angle MAD$$(AM-биссектриса ); $$\angle MAD=\angle BMA$$(накрест лежащие) $$\Rightarrow \angle BAM=\angle BMA\Rightarrow$$ $$\Delta ABM$$ - равнобедренный
3)Аналогично $$\Delta MCD$$ - равнобедренный $$\Rightarrow$$ $$AB=BM; MC=CD$$, но $$AB=CD\Rightarrow BM=MO$$
Задание 26
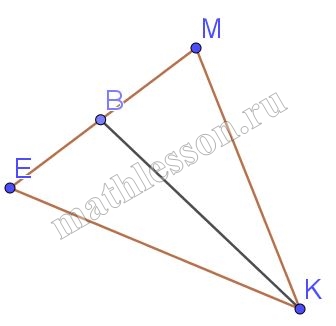
В треугольнике КЕМ длина стороны КЕ равна 27, длина биссектрисы КВ равна 24, а длина отрезка МВ равна 8. Найдите периметр треугольника КМВ.
1) Пусть KE=a=27; KM=b; EB=x; BM=y=8; KB=m=24; $$\angle EKB=\angle BKM=\alpha$$
2) По свойству биссектрисы: $$\frac{x}{y}=\frac{a}{b}(1)$$
3) Рассмотрим теорему косинусов для $$\Delta EBK$$ и $$\Delta BMK$$:
$$\left\{\begin{matrix}y^{2}=m^{2}+b^{2}-2mb \cos \alpha\\x^{2}=m^{2}+a^{2}-2ma \cos \alpha\end{matrix}\right.$$
Умножим первое и второе уравнения на a и b соответственно и вычтем из первого второе :
$$\left\{\begin{matrix}y^{2}a =m^{2}a+b^{2}a-2mab \cos \alpha\\x^{2}b=m^{2}b+a^{2}b-2mab \cos \alpha\end{matrix}\right.$$
Получим: $$y^{2}a-x^{2}b=m^{2}a+b^{2}a-m^{2}b-a^{2}b$$
Рассмотрим левую часть равенства: $$y^{2}a-x^{2}b=xy(\frac{ya}{x}-\frac{xb}{y})$$ .С учетом , что $$\frac{x}{y}=\frac{a}{b}$$, получим : $$xy(\frac{b}{a}*a-\frac{a}{b}*b)=xy(b-a).$$
Рассмотрим правую часть равенства: $$m^{2}a+b^{2}a-m^{2}b-a^{2}b=m^{2}(a-b)-ba(a-b)$$. Получим : $$xy(b-a)=m^{2}(a-b)-ba(a-b)$$.
Т.к. $$a\neq b$$ (иначе получим равнобедренный), то поделим $$a-b$$: $$-xy=m^{2}-ba\Rightarrow m^{2}=ab-xy(2)$$ - вообще, это формула длины биссектриссы через две стороны и отрезки третьей, но в учебниках за 7-9 класс ее не встречал, потому необходимо ее выводить.
4) Итого имеем систему: $$\left\{\begin{matrix}\frac{x}{y}=\frac{a}{b}\\m^{2}=ab-xy\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{x}{8}=\frac{27}{b}\\24^{2}=27b-8x\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{216}{b}\\576=27b-\frac{8*216}{b}\end{matrix}\right.$$
$$576b=27b^{2}-1728\Leftrightarrow$$ $$27b^{2}-576b-1728=0|:9\Leftrightarrow$$ $$3b^{2}-64b-192=0$$
$$D=4096+2304=6400$$
$$b_{1}=\frac{64+80}{6}=\frac{144}{6}=24$$
$$b_{2}=\frac{64-80}{6}<0$$
5) $$P_{BMK}=m+y+b=24+8+24=56$$