ОГЭ математика 2018. Разбор варианта Алекса Ларина № 181.

Найдите значение выражения $$\frac{25^{-5}\cdot 25^{-6}}{25^{-12}}$$

В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми. 

Какой вывод о суточном потреблении жиров, белков и углеводов женщиной можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 65 г жиров, 55 г белков и 275 г углеводов? В ответе укажите номера верных утверждений.

1. Потребление жиров в норме.

2. Потребление белков в норме.

3. Потребление углеводов в норме. 

На координатной прямой точками отмечены числа $$\frac{5}{11}$$, $$\frac{13}{7}$$, $$2,3$$, $$0,3$$

Какому числу соответствует точка C? 

 Варианты ответа:

1)$$\frac{5}{11}$$,

2) $$\frac{13}{7}$$,

3) $$2,3$$,

4) $$0,3$$

Какое из выражений равно степени $$2^{5+k}$$?

Варианты ответа:

1) $$\frac{2^{5}}{2^{k}}$$;

2) $$\frac{2^{5}}{2^{-k}}$$;

3) $$2^{5}+2^{k}$$;

4) $$(2^{5})^{k}$$

На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Найдите наименьшее значение температуры. Ответ дайте в градусах Цельсия.

Решите уравнение $$x(2-x)=1$$

В начале учебного года в школе было 480 учащихся, а к концу года их стало 600. На сколько процентов увеличилось число учащихся за учебный год число учащихся? 

На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей. 

Какие из следующих утверждений верны?

1. пользователей из Аргентины меньше, чем пользователей из Казахстана.

2. пользователей из Бразилии вдвое больше, чем пользователей из Аргентины.

3. примерно треть пользователей — не из Бразилии.

4. пользователей из Аргентины и Беларуси более 3 миллионов человек. 

В среднем из каждых 80 поступивших в продажу аккумуляторов 68 аккумуляторов заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен. 

График какой из приведенных ниже функций изображён на рисунке? 

Варианты ответа:

1) $$y=x^{2}-2$$;

2) $$y=-x^{2}+2$$;

3) $$y=x^{2}+4$$;

4) $$y=-x^{2}+4$$

Дана арифметическая прогрессия $$(a_{n})$$, для которой $$a_{4}=-18$$, $$a_{10}=-234$$. Найдите разность прогрессии. 

Упростите выражение $$\frac{b+2}{b^{2}+3b}-\frac{1+b}{b^{2}-9}$$ и найдите его значение при $$b=5$$.

Закон Менделеева–Клапейрона можно записать в виде $$PV=vRT$$, где P — давление (в паскалях), V — объём (в м³), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T=700 К, P=20941,2 Па, V=9,5 м³. 

 Укажите неравенство, которое не имеет решений: 

1) $$x^{2}-6x-38>0$$;

2) $$x^{2}-6x+38<0$$;

3) $$x^{2}-6x-38<0$$;

4) $$x^{2}-6x+38>0$$.

К вершинам двух столбов привязан гибкий шнур. На середину шнура сел аист, и шнур провис до земли. На каком расстоянии (в метрах) от столба высотой 3 метра аист коснулся земли, если высота второго столба 2 метра, а расстояние между ними 5 метров? 

Касательные в точках A и B к окружности с центром O пересекаются под углом $$68^{\circ}$$. Найдите угол ABO. Ответ дайте в градусах.

Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке Е. Найдите периметр параллелограмма, если BЕ=5, CЕ=14

В трапецию, сумма длин боковых сторон которой равна 52, вписана окружность. Найдите длину средней линии трапеции. 

В треугольнике ABC угол C равен $$90^{\circ}$$, CH — высота, BC=15, CH=9. Найдите $$\sin A$$. 

Какие из следующих утверждений верны? 
1. Если угол острый, то смежный с ним угол также является острым  

2. Сумма смежных углов равна 180°.

3. В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности. 
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов 

Решите систему уравнений $$\left\{\begin{matrix}x^{3}+xy^{2}=10\\y^{3}+x^{2}y=5\end{matrix}\right.$$

Дорога между пунктами А и В, длиной 36км, состоит из подъёма и спуска. Велосипедист, двигаясь на спуске со скоростью на 6км/ч большей, чем на подъёме, затрачивает на путь из А в В 2 ч 40 мин, а на обратный путь на 20 мин меньше. Найдите скорость велосипедиста на подъёме и на спуске.

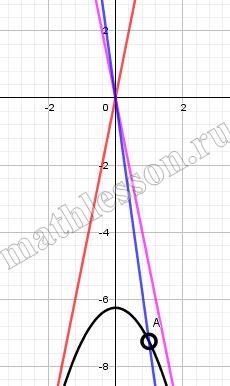
Постройте график функции $$y=\frac{(x^{2}+6,25)(x-1)}{1-x}$$ и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.

Углы, образуемые диагоналями ромба с одной из его сторон относятся как 2:3. Найдите углы ромба.

Докажите, что в прямоугольном треугольнике сумма катетов равна сумме диаметров вписанной и описанной окружностей.

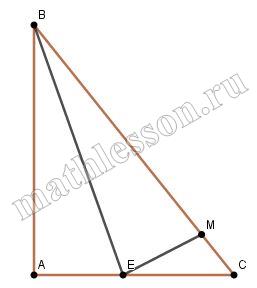
В прямоугольном треугольнике ABC проведена биссектриса ВЕ, а на гипотенузе ВС взята точка М так, что $$EM \perp BE$$. Найдите площадь треугольника АВС, если СМ=1, СЕ=2..