ОГЭ математика 2018. Разбор варианта Алекса Ларина № 183.
Решаем ОГЭ 183 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №183 (alexlarin.com)
Решаем ОГЭ 183 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №183 (alexlarin.com)
Задание 1
Найдите значение выражения $$\frac{1}{\frac{1}{30}+\frac{1}{42}}$$
$$\frac{1}{\frac{1}{30}+\frac{1}{42}}=$$$$\frac{1}{\frac{1}{5*6}+\frac{1}{7*6}}=$$$$\frac{1}{\frac{5+7}{5*6*7}}=$$$$\frac{5*6*7}{12}=17,5$$
Задание 2
|
Магазин
|
Орехи (за кг)
|
Щоколад (за плитку)
|
Зефир (за кг)
|
|
"Ладья"
|
600
|
45
|
144
|
|
"Восторг"
|
585
|
65
|
116
|
|
"Галатея"
|
660
|
53
|
225
|
1) В «Ладье»:$$(600*0,6+45*6+144*2,5)*0,9=891$$ 2) B «Восторге»:$$585*0,6+65*6+116*2,5=1031$$ 3) B «Галатее»:$$(660*0,6+225*2,5)*0,8+53*6=1084,8$$ Наименьшая цена в "Ладье", что соответствует 1 варианту ответа
Задание 3
На координатной прямой отмечено число a. Найдите наибольшее из чисел $$a^{2}$$, $$a^{3}$$, $$a^{4}$$
Число $$a$$ меньше -1, пусть $$a=-2$$, тогда $$a^{2}=4 ; a^{-3}=-8 ; a^{4}=16$$. Наибольшее значение соответствует $$a^{4}$$ или 3 варианту ответа
Задание 4
Найдите значение выражения $$\sqrt{0,03}\cdot\frac{1}{\sqrt{75}}$$
$$\sqrt{0,03}\cdot\frac{1}{\sqrt{75}}=$$$$\sqrt{\frac{3}{100}*\frac{1}{75}}=$$$$\sqrt{\frac{1}{10^{2}*5^{2}}}=$$$$\frac{1}{10*5}=0,02$$, что соответствует 3 варианту ответа
Задание 5
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры за сутки.
$$max = 1 ; min = -10$$, тогда $$max - min = 1-(-10)=11$$
Задание 6
Решите уравнение $$4x^{2}-5(x-1)+9x-4=0$$
$$4x^{2}-5(x-1)+9x-4=0 \Leftrightarrow$$$$4x^{2}-5x+5+9x-4=0 \Leftrightarrow$$$$4x^{2}+4x+1=0\Leftrightarrow$$$$(2x+1)^{2}=0\Leftrightarrow$$$$x=-0,5$$
Задание 7
В начале года число абонентов телефонной компании «Берег» составляло 800 тыс. чел., а в конце года их стало 900 тыс. чел. На сколько процентов увеличилось за год число абонентов этой компании?
Изменение составило: $$900-800=100$$ тыс. Первоначальное число ( с которым сравнивают ) принимаем за 100%, тогда 100 - x % 800 - 100% 100 - x% $$x=\frac{100*100}{800}=12,5$$
Задание 8
На В магазине продаются футболки пяти размеров: XS, S, M, L и XL. Данные по продажам в июне представлены на круговой диаграмме.
1. Больше всего было продано футболок размера S
1. Больше всего было продано футболок размера S - неверно, сегмент, соответствующий данному размеру не самый большой по площади 2. Меньше 30% проданных футболок — футболки размеров L и XL - неверно, в сумме их сегменты составляют больше 30% от круга 3. Футболок размеров S и XS вместе продано больше 30 - верно, так как 30 составляет четвертую часть от 120, а сумма их сегментов больше четверти круга 4. Футболок размера XL было продано меньше 30 штук - верно (аналогично 3)
Задание 9
В турнире участвуют 6 футбольных клубов: «Витязь», «Парнас», «Сириус», «Бекас», «Нептун» и «Буревестник». Команды случайным образом распределяют на две группы по три команды. Какова вероятность того, что «Парнас» и «Сириус» окажутся в одной группе?
Групп 2, команд 6, значит в одной группе будет 3 команды. Пусть "Парнас" уже находится в какой - то группе, тогда свободных мест в ней остается 2, а команд остается 5. Следовательно, вероятность, что "Сириус" попадет в эту же группу: $$P=\frac{2}{5}=0,4$$
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают.
ФОРМУЛЫ:
1) $$y=-\frac{4}{x}$$;
2) $$y=2x+4$$;
3) $$y=2x^{2}$$;
4) $$y=\frac{4}{x}$$
А: Представлена линейная функция, общий вид которой $$y=ax+b$$. Данному вида соответствует вариант под номером 2 Б: Представлена квадратичная функция, вид которой для данного графика выглядит как $$y=ax^{2}$$. Ему соответствует 3 вариант. В: Представлена обратная пропорциональность, вид которой для данного графика $$y=-\frac{k}{x}$$ (так как располагается во второй и третьей координатных четвертях). Ему соответствует 1 вариант ответа.
Задание 11
Дана геометрическая прогрессия 8, 20, ... Какое число стоит в этой последовательности на 5-м месте?
Найдем знаменатель геометрической прогрессии: $$q=\frac{b_{n+1}}{b_{n}}=\frac{20}{8}=2,5$$. Найдем пятый член геометрической прогрессии: $$b_{n}=b_{1}*q^{n-1}=8*2,5^{5-1}=312,5$$
Задание 12
Найдите значение выражения $$\frac{1}{4x}-\frac{4x+y}{4xy}$$ при $$x=\frac{1}{2}$$; $$y=\frac{1}{3}$$
$$\frac{1}{4x}-\frac{4x+y}{4xy}=$$$$\frac{y}{4xy}-\frac{4x+y}{4xy}=$$$$\frac{y-4x-y}{4xy}=$$$$\frac{-4x}{4xy}=$$$$\frac{-1}{y}=$$$$\frac{-1}{\frac{1}{3}}=-3$$
Задание 13
Период колебания математического маятника (в секундах) приближённо можно вычислить по формуле $$T=2\sqrt{l}$$ , где l — длина нити в метрах. Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 15 секунд.
$$T=2\sqrt{l} \Rightarrow$$$$\sqrt{l}=\frac{T}{2} \Rightarrow$$$$l=(\frac{T}{2})^{2}=$$$$(\frac{15}{2})^{2}=56,25$$
Задание 14
$$x^{2}+5x\leq0 \Leftrightarrow$$$$x(x+5)\leq0 \Leftrightarrow$$$$\left\{\begin{matrix}x\geq -5\\ x\leq 0\end{matrix}\right.\Leftrightarrow$$$$x \in [-5;0]$$, что соответствует 2 варианту ответа
Задание 15
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 18 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними через 5 часов?
Первый пройдет за 5 часов : $$18*5=90$$км , а второй $$24*5=120$$км. По теореме Пифагора расстояние между ними: $$S=\sqrt{120^{2}+90^{2}}=150$$км
Задание 16
Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором $$AB=BC$$ и $$\angle ABC=108^{\circ}$$. Найдите величину угла ВОС. Ответ дайте в градусах.
Из треугольника $$ABC$$: $$\angle BAC = \frac{180-108}{2}=36$$ ( так как треугольник равнобедренный ). $$\angle BOC$$ является центральным, и он опирается на ту же дугу, что и вписанный $$\angle BAC$$, то есть он в два раза больше последнего: $$36*2=72$$
Задание 17
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=10 и BC=BM. Найдите AH.
1) BM = BC, значит треугольник BMC - равнобедренный, тогда BH - высота и медиана, тогда MH=HC=0,5MC 2)AM=MC=0,5AC ( так как BM - медиана ), тогда MH = 0,25AC , и AH = 0,75AC = 0,75*10 = 7,5
Задание 18
Площадь трапеции вычисляется как полусумму оснований на высоту: $$S = \frac{7+9+12}{2}*12=168$$
Задание 19
$$AB = \sqrt{AC^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}}=5$$ $$sin \angle ABC = \frac{AC}{AB}=\frac{3}{5}=0,6$$
Задание 20
1. В прямоугольном треугольнике тангенс одного из углов равен 0.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
1. В прямоугольном треугольнике тангенс одного из углов равен 0 - неверно, в таком случае один из углов 0 или 180 градусов 2. Во всяком треугольнике против большей стороны лежит угол $$90^{\circ}$$ - неверно, против большей стороны лежит больший угол, но не обязательно 90 градусов 3. Внешний угол треугольника равен сумме углов треугольника, не смежных с ним - верно
Задание 21
Решите уравнение $$\frac{6}{(x+1)(x+2)}+\frac{8}{(x-1)(x+4)}=1$$
$$\frac{6}{(x+1)(x+2)}+\frac{8}{(x-1)(x+4)}=1$$ ОДЗ: $$\left\{\begin{matrix}x+1\neq 0\\ x+2\neq 0\\ x-1\neq 0\\ x+4\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}x\neq -1\\ x\neq -2\\ x\neq 1\\ x\neq -4\end{matrix}\right.$$ Раскроем скобки в знаменателях: $$\frac{6}{(x^{2}+3x+2}+\frac{8}{(x^{2}+3x-4}=1$$ Пусть $$x^{2}+3x+2=y$$ , тогда $$x^{2}+3x-4=x^{2}+3x+2-6=y-6$$ $$\frac{6}{y}+\frac{8}{y-6}=1\Leftrightarrow $$ $$6(y-6)+8y=y(y-6)\Leftrightarrow $$ $$6y-36+8y-y^{2}+6y=0|\cdot(-1)\Leftrightarrow $$ $$y^{2}-20y+36=0\Leftrightarrow $$ $$D=400-144=256=16^{2}$$ $$\left [ \begin{matrix}y_{1}=\frac{20+16}{2}=18\\ y_{2}=\frac{20-16}{2}=2\end{matrix}\right.\Leftrightarrow $$ $$\left [ \begin{matrix}x^{2}+3x+2=18\\ x^{2}+3x+2=2\end{matrix}\right.\Leftrightarrow $$$$ \left [ \begin{matrix}x^{2}+3x-16=0(1) \\ x^{2}+3x=0(2) \end{matrix}\right.$$ $$1)x^{2}+3x-16=0$$ $$D=9+64=73$$ $$x_{1,2}=\frac{-3\pm \sqrt{73}}{2}$$ $$2)x^{2}+3x=0\Leftrightarrow $$$$x(x+3)=0 \Leftrightarrow $$$$x=0 ; x=-3$$
Задание 22
Из города А в город В с интервалом в 10 мин отправились три рейсовых автобуса. Первый автобус шел со скоростью на 5 км/ч меньше положенной, второй сохранял положенную скорость, а третий превышал ее на 6 км/ч. В результате все три автобуса пришли в Б одновременно. Определите расстояние между городами A и B.
Пусть скорость второго равна x км/ч, тогда скорость первого х-5 км/ч, скорость третьего х+6 км/ч. Пусть S - расстояние от А до В в км. Тогда: $$t_{1}=\frac{S}{x-5}$$ - время первого $$t_{2}=\frac{S}{x}$$ - время второго $$t_{3}=\frac{S}{x+6}$$ - время третьего Разница во времени у них составляет 10 минут, то есть $$\frac{1}{6}$$ часа. Получаем систему: $$\left\{\begin{matrix}t_{1}-t_{2}=\frac{1}{6}\\t_{2}-t_{3}= \frac{1}{6}\end{matrix}\right.$$ Подставим имеющиеся выражения: $$\left\{\begin{matrix}\frac{S}{x-5}-\frac{S}{x}=\frac{1}{6}\\\frac{S}{x}-\frac{S}{x+6}= \frac{1}{6}\end{matrix}\right.\Leftrightarrow $$ $$\left\{\begin{matrix}\frac{S(x-(x-5))}{(x(x-5)}=\frac{1}{6}\\\frac{S((x+6)-x)}{x(x+6)}= \frac{1}{6}\end{matrix}\right.$$ Поделим первое на второе: $$\frac{5}{x(x-5)} : \frac{6}{x(x+6)}= 1 \Leftrightarrow $$$$\frac{5(x+6)}{6(x-5)}=1 \Leftrightarrow $$$$5x+30=6x-30 \Leftrightarrow $$$$x=60$$ Подставим полученное значение в первое уравнение: $$\frac{S*5}{60*55}=\frac{1}{6} \Leftrightarrow $$$$30S=60*55 |:30 \Leftrightarrow$$$$S=110$$
Задание 23
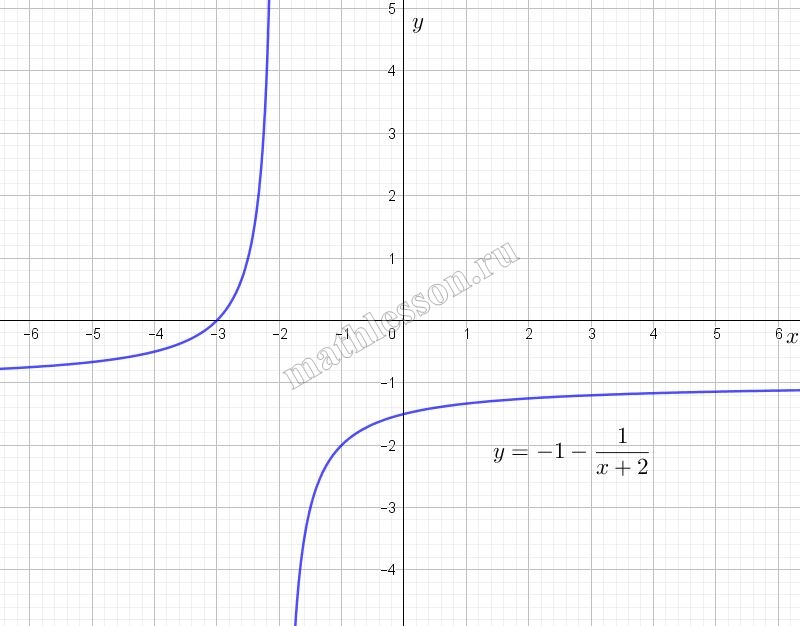
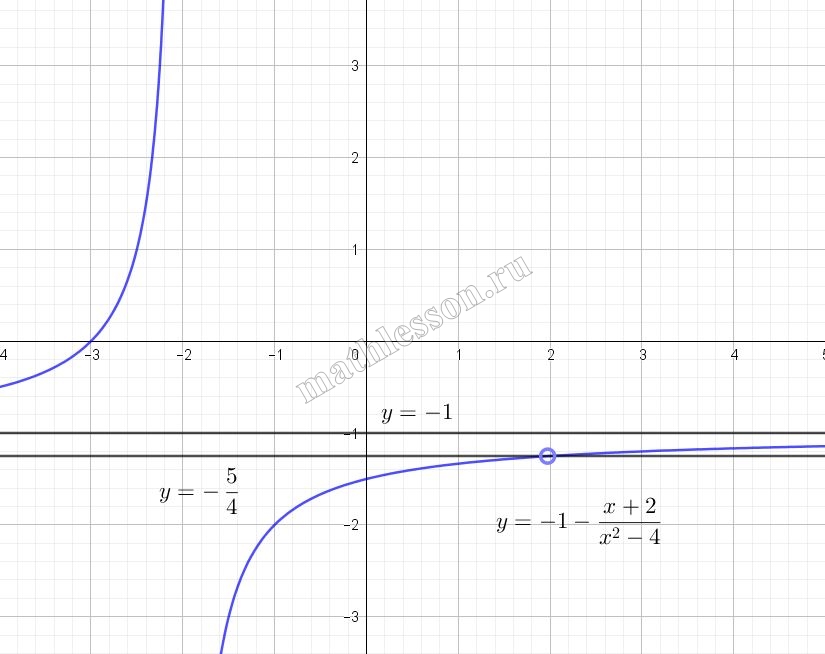
Постройте график функции $$y=-1-\frac{x-2}{x^{2}-4}$$ и определите, при каких значениях $$a$$ прямая $$y=a$$ не имеет с графиком ни одной общей точки.
ОДЗ: $$x^{2}-4 \neq 0 \Leftrightarrow$$$$x\neq\pm 2$$. Преобразуем правую часть функции: $$-1-\frac{x-2}{x^{2}-4}=$$$$-1-\frac{x-2}{(x-2)(x+2)}=$$$$-1-\frac{1}{x+2}$$
То есть график функции $$y_{1}=-1-\frac{1}{x+2}$$ и график искомой функции совпадают, если к $$y_{1}$$ применить ОДЗ для искомой. График функции $$y_{1}$$ - гипербола, смещенная на 1 единицу вних и на две влево относительно графика эталонной обратной пропорциональности $$y=\frac{1}{x}$$. Начертим график функции $$y_{1}$$:
Учтем, что $$x\neq\pm 2$$. В случае $$x\neq -2$$ можно отдельно не рассматривать, так как это условие уже выполняется для графика функции $$y_{1}$$. Для $$x\neq 2$$: подставим значение $$x=2$$ в функции $$y_{1}$$: $$y_{1}(2)=-1-\frac{1}{2+2}=-\frac{5}{4}$$. То есть точку, с координатами $$(2;-\frac{5}{4})$$ необходимо отметить пустой на графике функции $$y_{1}$$ и тогда мы получим график искомой функции:
Прямая $$y=a$$ - прямая паралленая оси Ох, чтобы она не имела с графиком искомой функции точек пересечения она должны использоваться следующие значения $$a=-1;-\frac{5}{4}$$:
Задание 24
Одна из сторон параллелограмма равна $$4\sqrt{3}$$ см, его площадь равна 12 см2, а острый угол между сторонами равен $$60^{\circ}$$. Найдите длину другой стороны параллелограмма.
Площадь параллелограмма вычисляется как произведение длин сторон на синус угла между ними. Пусть х - вторая сторона. Тогда; $$4\sqrt{3} * x * \sin 60^{\circ}=12 \Leftrightarrow$$$$x=\frac{12}{4\sqrt{3}*\frac{\sqrt{3}}{2}}=2$$
Задание 25
В выпуклом четырёхугольнике ABCD углы DAC и DBC равны. Докажите, что углы CDB и САВ также равны.
1) $$\angle CBD=\angle CAD$$ они опираются на $$CD$$ $$\Rightarrow$$ $$ABCD$$ можно вписать в окружность
2) $$\angle CDB$$ и $$\angle CAB$$ опираются на $$BC$$ и из пункта 1 получаем, что они вписанные $$\Rightarrow$$ т.к. на одну хорду опираются, то $$\angle CDB=\angle CAB$$
ч.т.д.
Задание 26
Сторона равностороннего треугольника АВС равна 14. Через его центр проведена прямая $$l$$, пересекающая сторону ВС и проходящая на расстоянии $$\sqrt{7}$$ от середины стороны АВ. В каком отношении прямая $$l$$ делит сторону ВС?