ОГЭ математика 2022. Разбор варианта Алекса Ларина № 297.
Больше разборов на моем ютуб-канале
Задания 1-5
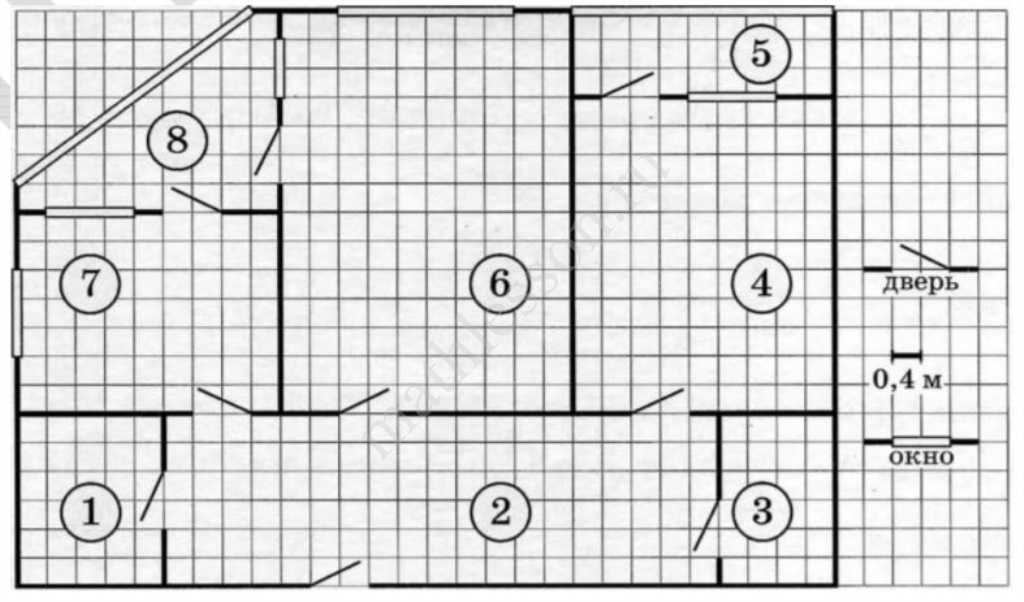
На рисунке (см. выше) изображён план двухкомнатной квартиры в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна, а также указано, что длина стороны клетки на плане соответствует 0,4 м. Вход в квартиру находится в прихожей. Слева от входа в квартиру располагаются кухня и санузел, а также одна из лоджий, в которую можно попасть из кухни. В эту же лоджию можно пройти и из гостиной. Наименьшую площадь имеет кладовая. В квартире есть ещё одна лоджия, куда можно попасть из прихожей, пройдя через спальню.
1. Для помещений, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность пяти цифр без пробелов, запятых и других разделительных символов.
| Помещения | кухня | спальня | гостиная | кладовая | прихожая |
| Цифры |
2. Найдите площадь (в м2) гостиной.
3. Найдите ширину (в метрах) остекления той лоджии, которая примыкает к кухне.
4. Плитка для пола размером 20 см × 20 см продаётся в упаковках по 8 штук. Сколько упаковок плитки необходимо купить, чтобы выложить пол кухни?
5. На сколько процентов площадь кухни меньше площади гостиной?
Задание 10
В группе из 20 российских туристов несколько человек владеют иностранными языками. Из них пятеро говорят только по‐английски, трое только по‐французски, двое по‐французски и по‐английски. Какова вероятность того, что случайно выбранный турист говорит по‐французски?
Задание 11
Ниже представлены графики функции вида $$y=ax^{2}+c$$. Установите соответствие между графиками и знаками коэффициентов a и c. В ответе укажите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.
- $$a<0, c<0$$
- $$a<0, c>0$$
- $$a>0, c<0$$
- $$a>0, c>0$$
Задание 12
Закон всемирного тяготения можно записать в виде $$F=\gamma\frac{m_{1}m_{2}}{r^{2}} $$, где F – сила притяжения между телами (в ньютонах), m1 и m2 – массы тел (в килограммах), r – расстояние между центрами масс тел (в метрах), а $$\gamma$$ – гравитационная постоянная, равная 6,67∙10-11H∙м2/кг2. Пользуясь этой формулой, найдите массу тела m1 в килограммах , если F=4,002 H, m2=4∙109 кг, r=2 м.
Задание 14
Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика в пятый день?
Задание 19
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.
- Один из углов треугольника всегда не превышает 60 градусов.
- Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
- Все диаметры окружности равны между собой
Задание 24
Окружности с центрами в точках O1 и O2 не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении m:n. Докажите, что диаметры этих окружностей относятся как m:n.