ОГЭ математика 2019. Разбор варианта Алекса Ларина № 193.
Решаем ОГЭ 193 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №193 (alexlarin.com)
Решаем ОГЭ 193 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №193 (alexlarin.com)
Задание 1
Найдите значение выражения $$(\frac{1}{9})^{-2}+19^{-3}:19^{-4}-2019$$
$$(\frac{1}{9})^{-2}+19^{-3}: 19^{-4}-2019=$$$$9^{2}+19^{-3-(-4)}-2019=61+19-2019=$$$$100-2019=1919$$
Задание 2
Для квартиры площадью 56 кв. м заказан натяжной потолок белого цвета. Стоимость работ по установке натяжных потолков приведена в таблице.
|
Цвет потолка |
Цена в рублях за 1 м2 (в зависмости от площали помещения) |
|||
|
до 10 м2 |
от 11 до 30 м2 |
от 31 до 60 м2 |
свыше 60 м2 |
|
|
белый |
1200 |
1000 |
800 |
600 |
|
цветной |
1350 |
1150 |
950 |
750 |
Какова стоимость заказа, если действует сезонная скидка в 5%?
В ответе укажите номер правильного варианта.
1) 4256 рублей
2) 44800 рублей
3) 42 560 рублей
4) 44 995 рублей
56*800=44800-стоимость без скидки 44800*0,95=42560-со скидкой, что соответствует 3 варианту ответа
Задание 3
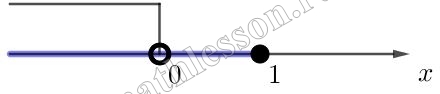
На координатной прямой отмечены числа a, b и c.
Какое из следующих утверждений об этих числах верно?
- $$a+b<c$$
- $$ab>c$$
- $$bc>1$$
- $$\frac{1}{c}<1$$
По условию задания: a<0<b<c<1. Пусть a=-0,5; b=0,4; c=0,8
- $$a+b<c\Leftrightarrow -0,5+0,4<0,8$$-верно
- $$ab>c-0,5*0,4>0,8$$-неверно
- $$bc>10,4*0,8>1$$-неверно
- $$\frac{1}{c}<1\frac{1}{0,8}<1$$-неверно
Верным является только первый вариант ответа
Задание 4
Значение какого из выражений является числом рациональным?
Варианты ответа
- $$\sqrt{8}*\sqrt{12}$$
- $$(\sqrt{8}-\sqrt{12})(\sqrt{8}+\sqrt{12})$$
- $$\frac{\sqrt{8}}{\sqrt{12}}$$
- $$(\sqrt{8}+\sqrt{12})^{2}$$
- $$\sqrt{8-12}=\sqrt{96}$$-иррационально
- $$(\sqrt{8}-\sqrt{12})(\sqrt{8}+\sqrt{12})=8-12=-4$$
- $$\frac{\sqrt{8}}{\sqrt{12}}=\sqrt{\frac{2}{3}}$$-иррационально
- $$(\sqrt{8}+\sqrt{12})^{2}=8+2\sqrt{96}+12$$-иррационально
Рациональным является только второй вариант ответа
Задание 5
На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 20 минут дебатов?
Кандидат A: 15 Кандидат Б: 10 В сумме : 15+10=25
Задание 6
Решите уравнение $$\frac{9}{x-5}=\frac{5}{x-9}$$
$$9(x-9)=5(x-5)\Leftrightarrow$$ $$9x-81=5x-25\Leftrightarrow$$ $$4x=56\Leftrightarrow$$ $$x=14$$
Задание 7
В в школе учится 1200 учащихся, среди которых 156 отличников. Сколько процентов составляют отличники этой школы?
1200-100% 156-x% $$x=\frac{156*100}{1200}=13$$
Задание 8
На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей.
Какие из следующих утверждений неверны?
- пользователей из Аргентины больше, чем пользователей из Польши.
- пользователей из Аргентины примерно втрое больше, чем пользователей из Парагвая.
- пользователей из Аргентины и Беларуси вместе — меньше четверти общего числа пользователей.
- пользователей из Бразилии примерно 8 миллионов человек
- верно
- не верно
- не верно
- верно
Задание 9
Аня выбирает трехзначное число. Найдите вероятность того, что оно делится на 11
Количество чисел до 999 делящихся на 11: $$999*11=90,(81)\Rightarrow 90$$ До 99 - 99:11=9 Всего трехзначных чисел: 999-99=900 $$P=\frac{90-9}{900}=\frac{81}{900}=0,09$$
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают.
функции
- $$y=-\frac{6}{x}$$
- $$y=-\frac{1}{2}x^{2}$$
- $$y=\frac{1}{2}x-2$$
- $$y=-\frac{1}{2}x^{2}-2$$
A - линейная функция $$\Rightarrow 3$$
Б - обратная пропорциональность $$\Rightarrow 1$$
B - квадратичная вида $$y=-ax^{2}\Rightarrow 2$$
Задание 11
Выписаны первые три члена арифметической прогрессии: 20; 13; 6; … Найдите шестой член этой прогрессии.
Найдем разность арифм. Прогрессии : $$d=a_{n+1}-a_{n}=13-20=-7$$ Найдем шестой член используя формулу n-го члена: $$a_{n}=a_{1}+d(n-1)$$ $$a_{6}=2a-7(6-1)=-15$$
Задание 12
Найдите значение выражения $$(x-5)^{2}-x(10+x)$$ при $$x=-\frac{1}{20}$$
$$(x-5)^{2}-x(10+x)=$$$$x^{2}-10x+25-10x-x^{2}=$$$$-20+25=-20(-\frac{1}{20})+25=26$$
Задание 13
Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T=700 K, P = 20 941,2 Па, V = 9,5 м3.
Выразим количество вещества из формулы: $$v=\frac{PV}{RT}$$ Найдем значение количества вещества: $$v=\frac{20941,2*9,5}{8,31*700}=\frac{209412*95*10^{-2}}{831*700*10^{-2}}=\frac{252*95}{700}=34,2$$
Задание 14
Решите неравенство $$9x^{2}-(3x-5)^{2}\leq 5(3x+4)$$
Варианты ответа:
- $$[3;+\infty)$$
- $$[-3;+\infty)$$
- $$(-\infty;3]$$
- $$(-\infty;-3]$$
$$9x^{2}-(3x-5)^{2}\leq 5(3x+4)\Leftrightarrow$$$$9x^{2}-9x^{2}+30x-25-25x-20\leq 0$$$$15\leq 45\Leftrightarrow x\leq 3$$, что соответствует 3 варианту ответа
Задание 15
Площадь квадрата: $$8^{2}=64$$ Площадь прямоугольника: $$5*3=15$$ $$S=64-15=49$$
Задание 17
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 5 и 8. Найдите длину основания BC.
Пусть $$BH_{1}\left | \right |CH$$ и $$BH_{1}=CH$$
Тогда $$AH_{1}=DH=5$$
$$HH_{1}=AH-AH_{1}=8-5=3=BC$$
Задание 19
Катеты прямоугольного треугольника равны $$5\sqrt{3}$$ и 5. Найдите синус наименьшего угла этого треугольника.
$$CB>AC\Rightarrow \angle B<\angle A$$
$$AB=\sqrt{5^{2}+(5\sqrt{3})^{2}}=10$$
$$\sin A=\frac{AC}{AB}=\frac{5}{10}=0,5$$
Задание 20
Какие из следующих утверждений верны?
- Все равнобедренные треугольники подобны.
- Каждая из биссектрис равнобедренного треугольника является его высотой.
- Равнобедренный треугольник с углом 60 - равносторонний.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
1.нет - только с равными соответствующими друг другу углами 2.нет - только та, что выходит из вершины, противоположной основанию. 3.да
Задание 21
Решите неравенство $$\frac{(x+2)(x+1)}{x^{2}-|x|-2}\leq -3x$$
Область определения: $$x^{2}-|x|-2\neq 0\Leftrightarrow$$$$|x|\neq 2, |x|\neq -1\Leftrightarrow$$$$x\neq \pm 2$$
Раскроем модуль:
1) При $$x\geq 0 \Rightarrow$$ $$\frac{(x+2)(x+1)}{x^{2}-x-2} \leq -3x\Leftrightarrow$$ $$\frac{(x+2)(x-1)}{(x-2)(x+1)}\leq -3x\Leftrightarrow$$ $$\frac{x+2}{x-2}+3x\leq 0$$
Рассматриваем числитель дроби, чтобы разбить его на множители: $$3x^{2}-5x+2=0$$
$$D=25-24=1$$
$$x_{1}=\frac{5+1}{6}=1$$
$$x_{2}=\frac{5-1}{6}=\frac{2}{3}$$
Следовательно,$$\frac{(x-\frac{2}{3})(x+1)}{x-2}\leq 0$$
2) При $$x<0 \Rightarrow$$$$\frac{(x+2)(x+1)}{x^{2}+x-2}\leq -3x\Leftrightarrow$$ $$\frac{(x+2)(x+1)}{(x+2)(x-1)}+3x\leq 0\Leftrightarrow$$$$\frac{x+1}{x-1}+3x\leq 0\Leftrightarrow$$ $$\frac{x+1+3x^{2}-3x}{x-1}\leq 0\Leftrightarrow$$ $$\frac{3x^{2}-2x+1}{x-1}\leq 0$$
Рассмотрим числитель полученной дроби:
$$3x^{2}-2x+1=0$$
$$D=4-12<0$$
Следовательно, числитель данной дроби всегда положителен и не влияет на знак неравенства: $$\frac{1}{x-1}\leq 0$$
С учетом обрасти опредеделения:
$$x \in (-\infty ;-2)\cup(-2;\frac{2}{3})\cup [1; 2)$$
Задание 22
Моторная лодка спустилась вниз по течению реки на 20 км и поднялась вверх по притоку еще на 10 км, затратив на весь путь 1 ч 10 мин. На обратный путь лодке потребовалось 1 ч 20 мин. Зная, что скорость реки равна скорости течения притока, найти собственную скорость лодки.
Пусть x-скорость лодки в стоячей воде (км\ч ),y км\ч - скорость течения
$$\left\{\begin{matrix}\frac{20}{x+y}+\frac{10}{x-y} =1\frac{1}{6} \\\frac{10}{x+y}+\frac{20}{x-y}=1\frac{1}{3} \end{matrix}\right.$$
Умножим второе на 2 и вычтем из первого:
$$\frac{10}{x-y}-\frac{40}{x-y}=\frac{7}{6}-\frac{8}{3}$$
$$-\frac{30}{x-y}=\frac{7-16}{6}=-\frac{9}{6}=-\frac{3}{2}$$
$$x-y=\frac{39*2}{3}=20$$
$$y=x-20$$
Подставим в первое:
$$\frac{20}{x+x-20}+\frac{10}{x-x+20}=\frac{7}{6}$$
$$\frac{20}{2x-20}+\frac{1}{2}=\frac{7}{6}$$
$$\frac{10}{x-10}=\frac{7-3}{6}=\frac{2}{3}$$
$$2(x-10)=30\Leftrightarrow$$ $$2x-20=30\Leftrightarrow$$ $$2x=50\Leftrightarrow$$ $$x=25$$
Задание 23
При каких значениях р вершины парабол $$y=x^{2}-6px+p$$ и $$y=-x^{2}+2px+3$$ расположены по одну сторону от оси х?
Вершина $$y=x^{2}-6px+p$$: $$x_{01}=-\frac{6p}{2}=3p$$, $$y_{01}=9p^{2}-18p^{2}+p=p-9p^{2}$$
Вершина $$y=-x^{2}+2px+3$$: $$x_{02}=-\frac{2p}{-2}=p$$, $$y_{02}=-p^{2}+2p^{2}+3=p^{2}+3$$
По одну сторону от OX:
$$\left[\begin{matrix}\left\{\begin{matrix}y_{01}>0\\y_{02}>0\end{matrix}\right.\\\left\{\begin{matrix}y_{01}<0\\y_{02}<0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$$$\left[\begin{matrix}\left\{\begin{matrix}p-9p^{2}>0 \\p^{2}+3>0 \end{matrix}\right. \\\left\{\begin{matrix}p-9p^{2}<0 \\p^{2}+3<0 \end{matrix}\right. \end{matrix}\right.\Leftrightarrow$$$$\left[\begin{matrix}\left\{\begin{matrix}p-9p^{2}>0 \\p \in R \end{matrix}\right. \\\left\{\begin{matrix}p-9p^{2}<0 \\p \in \varnothing \end{matrix}\right. \end{matrix}\right.\Leftrightarrow$$$$p(1-9p)>0\Leftrightarrow$$ $$p\in (0 ;\frac{1}{9})$$
Задание 24
В прямоугольном треугольнике, периметр которого равен 36 см, вписана окружность. Гипотенуза делится точкой касания в отношении 2 : 3. Найдите длину гипотенузы.

1) Пусть $$\frac{AH}{HB}=\frac{2}{3}$$, тогда AH=2x; HB=3x
2) По свойству касательных MB=HB=3x, NA=AH=2x
3) Пусть ON=OH=OM=y, но NC=CM=y. Тогда по т. Пифагора :$$(y+2x)^{2}+(y+3x)^{2}=(5x)^{2}(1)$$
4) т.к. P=36, то $$y+2x+y+3x+5x=36$$, $$2y=36-10x\Leftrightarrow y=18-5x$$
Подставим в (1)
$$(18-5x+2x)^{2}+(18-5x+3x)^{2}=25x^{2}$$
$$324-108x+9x^{2}+324-72x+4x^{2}=25x^{2}$$
$$12x^{2}+180x-648=0$$
$$x^{2}+15x-54=0$$
$$\left\{\begin{matrix}x_{1}+x_{2}=-15\\x_{1}*x_{2}=-54\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=3\\x_{2}=-18\end{matrix}\right.$$
-18 не может быть, так как длина - число положительное, следовательно, $$5x=5*3=15$$ - длина гипотенузы
Задание 25
Докажите, что в прямоугольном треугольнике произведение длин отрезков, на которые делит гипотенузу точка касания с вписанной окружностью, равна площади треугольника.

1) Пусть AH=x; HB=y; NO=OM=OH=r. По свойству касательных: AN=AH=x, MB=HB=y
2) $$S_{ABC}=\frac{1}{2}AC*CB=$$$$\frac{1}{2}(x+r)(y+r)=$$$$\frac{1}{2}xy+\frac{1}{2}xr+\frac{1}{2}yr+\frac{1}{2}r^{2}(1)$$
С другой стороны : $$S_{ABC}=2S_{AOH}+2S_{HOB}+S_{CNOM}=$$$$2S_{AOB}+S_{CNOM}=2*\frac{1}{2}(x+y)r+r^{2}=xr+yr+r^{2}(2)$$
Приравняем (1) и (2):
$$\frac{1}{2}xy+\frac{1}{2}xr+\frac{1}{2}yr+\frac{1}{2}r^{2}=xr+yx+r^{2}$$
$$\frac{1}{2}xy=\frac{1}{2}xr+\frac{1}{2}yr+\frac{1}{2}r^{2}|*2$$
$$xy=xr+y^{2}+r^{2}=S_{ABC}$$
Задание 26
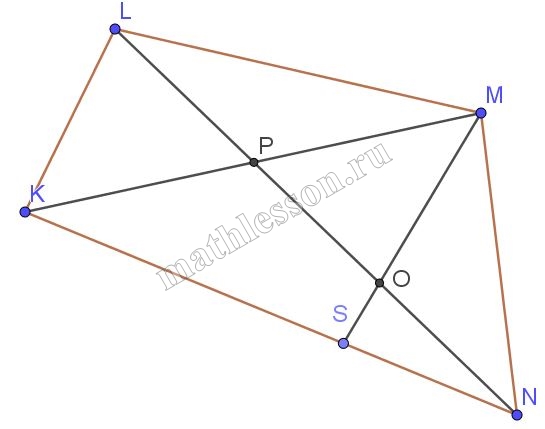
В выпуклом четырехугольнике KLMN отрезок MS, соединяющий вершину М с точкой S, расположенной на стороне КN, пересекает диагональ LN в точке О. Известно, что KL : MN = 6 : 7, KM : ON = 2 : 1 и $$\angle KLN + \angle KMN=180$$. Найдите отношение отрезков MO и OS.
1) Пусть $$KM\cap LN=P$$, $$\angle KLN=\alpha$$ , тогда $$\angle KMN=180-\alpha$$ ,$$\angle LPK=\angle MPN=\beta$$ (вертикальные)
2) из $$\Delta LPK$$ по теореме синусов: $$\frac{KP}{\sin \alpha }=\frac{LK}{\sin \beta }(1)$$
Из $$\Delta PMN : \frac{PN}{\sin (180-\alpha )}=\frac{MN}{\sin \beta }$$
С учетом , что $$\sin \alpha =\sin (180-\alpha )$$, получаем: $$\frac{PN}{\sin \alpha }=\frac{MN}{\sin \beta }(2)$$
Поделим (1) и (2): $$\frac{KP}{PN}=\frac{LK}{MN}=\frac{6}{7}$$
3) Пусть KM=2y; ON=y, тогда KP=6x, PN=7x, PM=2y-6x, PO=7x-y;
4)По т. Менелая из $$\Delta KPN$$ и секущей MS : $$\frac{MO}{OS}*\frac{SN}{NK}*\frac{KP}{PM}=1$$
Пусть $$\frac{SO}{OS}=m$$, тогда $$m*\frac{SN}{SN+SK}*\frac{6x}{2y-6x}=1(3)$$
По т. Менелая из $$\Delta KMS$$ и секущей NP: $$\frac{NO}{OP}*\frac{PM}{MK}*\frac{MS}{SN}=1$$
Пусть $$\frac{SK}{SN}=n$$, тогда $$\frac{SN}{SN+SK}=\frac{\frac{SN}{SN}}{\frac{SN}{SN}+\frac{SK}{SN}}=\frac{1}{1+n}$$
Получаем: $$\frac{y}{7x-y}*\frac{2y-6x}{2y}*n=1(4)$$
Выразим в (3) m: $$m=\frac{2y-6x}{6x}*(1+n)=\frac{(y-3x)(1+n)}{3x}(5)$$
Выразим в (4) n: $$n=\frac{y}{y-3x}*\frac{7x-y}{y}=\frac{7x-y}{y-3x}$$
Выразим в (5): $$m=\frac{(y-3x)(1+\frac{7x-y}{y-3x})}{3x}=$$$$\frac{y-3x+7x-y}{3x}=\frac{4x}{3x}=\frac{4}{3}$$