ОГЭ математика 2019. Разбор варианта Алекса Ларина № 203.
Решаем ОГЭ 203 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина № 203 (alexlarin.com)
Решаем ОГЭ 203 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина № 203 (alexlarin.com)
Задание 1
Найдите значение выражения $$5*10^{-1}+3*10^{-2}+1*10^{-4}$$
$$5* 10^{-1}+3*10^{-2}+1*10^{-4}=$$$$\frac{5}{10}+\frac{3}{100}+\frac{1}{10000}=0,5301$$
Задание 2
В таблице приведены нормативы по прыжкам с места для учеников 10 класса.
| Мальчики | Девочки | |||||
| Отметка | «5» | «4» | «3» | «5» | «4» | «3» |
| Расстояние, см | 230 | 220 | 200 | 185 | 170 | 155 |
Какую оценку получит девочка, прыгнувшая на 177 см?
Варианты ответа:
- «5»
- «4»
- «3»
- «Неудовлетворительно»
177 см попадает в диапазон [175;185), что соответствует оценке 4 или 2 варианту ответа
Задание 3
Между какими числами заключено число $$3\sqrt{3}$$?
Варианты ответа
- 5 и 6
- 6 и 7
- 8 и 9
- 9 и 10
Представим число в виде квадратного корня: $$3\sqrt{3}=\sqrt{3^{2}*3}=\sqrt{27}$$$$\Rightarrow$$$$\sqrt{25}<\sqrt{27}<\sqrt{36}$$$$\Leftrightarrow$$ $$5<3\sqrt{3}<6$$, что соответствует 1 варианту ответа
Задание 4
Найдите значение выражения $$\sqrt{3^{6}*4^{4}*5^{2}}$$
$$\sqrt{3^{6}*4^{4}*5^{2}}=$$$$3^{3}*4^{2}*5=27*16*5=2160$$
Задание 5
При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости. По горизонтальной оси откладывается скорость в километрах в час, по вертикальной — тормозной путь в метрах. Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 60 км/ч
Задание 6
Решите уравнение $$(x+3)^{2}=(x-13)^{2}$$
$$(x+3)^{2}=(x-13)^{2}$$$$\Leftrightarrow$$ $$(x+3)^{2}-(x-13)^{2}=0$$$$\Leftrightarrow$$ $$(x+3-(x-13))(x+3+(x-13))=0$$$$\Leftrightarrow$$ $$16*(2x-10)=0$$$$\Leftrightarrow$$ $$2x=10$$$$\Leftrightarrow$$ $$x=5$$
Задание 7
Магазин делает пенсионерам скидку на определённое количество процентов от цены покупки. Пачка масла стоит в магазине 105 рублей. Пенсионер заплатил за неё 84 рубля. Сколько процентов составляет скидка для пенсионеров?
Пусть 105руб. -100% , а 84 руб-x%. Составим пропорцию:
Тогда $$x=\frac{84*100}{105}=80$$% , следовательно, скидка составила $$100-80=20$$%
Задание 8
На диаграмме показан возрастной состав населения Китая.
Сколько примерно человек младше 14 лет проживает в Китае, если население Китая составляет 1,3 млрд человек?
Варианты ответа:
- около 100 млн
- около 260 млн
- около 325 млн
- около 150 млн
Сегмент группы до 14 лет составляет примерно пятую часть от круга. Следовательно, количество людей будет $$\frac{1300}{5}=260$$ млн, что соответствует 2 варианту ответ
Задание 9
В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайным образом. Вика покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Вика не найдет приз в своей банке
В одной из десяти есть приз, следовательно, в 9 из 10 – нет, тогда , вероятность не найти приз: $$P=\frac{9}{10}=0,9$$
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
ФОРМУЛЫ
- $$y=\frac{1}{9x}$$
- $$y=-\frac{1}{9x}$$
- $$y=-\frac{9}{x}$$
- $$y=\frac{9}{x}$$
Во всех случаях представлен график обратной пропорциональности ($$y=\frac{k}{x}$$). Если $$k>0$$, то график в 1 и 3 четвертях, $$k<0$$ - во 2 и 4. Если $$\left | k \right |>1$$, то идет расширение от точки (0;0), $$\left | k \right |<1$$ - сужение. Тогда:
Задание 11
Последовательность (an) задана условиями a1=2 , an+1=an+5. Найдите a10
Найдем разность арифметической прогрессии: $$d=a_{n+1}-a_{n}=a_{n}+5-a_{n}=5$$
Найдем 10-ый член: $$a_{n}=a_{1}+d(n-1)$$$$\Rightarrow$$ $$a_{10}=2+5(10-1)=47$$
Задание 12
Найдите значение выражения $$\frac{b-4}{b^{2}}:\frac{b-4}{b^{2}+4b}$$ при b=-0,5
$$\frac{b-4}{b^{2}}:\frac{b-4}{b^{2}+4b}=$$$$\frac{b-4}{b^{2}}*\frac{b(b+4)}{b-4}=$$$$\frac{b+4}{b}=\frac{-0,5+4}{-0,5}=-7$$
Задание 13
Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s=nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l=60 см, n=1200? Ответ выразите в километрах.
Найдем расстояние в см: $$S=60*1200=72 *10^{3}$$ см. С учетом , что 1 км.=$$10^{3}$$ м=$$10^{3}*10^{2}$$ см., получим : $$S=\frac{72*10^{3}}{10^{5}}=0,72$$ км.
Задание 14
На каком рисунке изображено множество решений системы неравенств $$\left\{\begin{matrix} -12+3x>0\\ 9-4x>-3\end{matrix}\right.$$
$$\left\{\begin{matrix} -12+3x>0\\ 9-4x>-3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix} 3x>12\\ 9+3x>4x\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix} x>4\\ x<3\end{matrix}\right.\Leftrightarrow$$ $$x \in \varnothing$$, что соответсвует 4 варианту .
Задание 15
На сколько градусов повернётся земля вокруг своей оси за 7 часов?
Полный оборот Земли вокруг своей оси (3600) происходит за 24 часа $$\Rightarrow$$ за 7 часов Земля повернется на $$\frac{360}{24}*7=105^{\circ}$$
Задание 16
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 65°. Найдите вписанный угол ACB. Ответ дайте в градусах.
1) $$\angle AOD=\angle BOC$$ (вертикальные)
2) $$\Delta BOC$$-равнобедренный (OB=OC –радиусы )$$\Rightarrow$$ $$\angle OCB=\angle OBC=\frac{180-\angle BOC}{2}=57,5$$
Задание 17
Основания трапеции равны 10 и 18. Найдите длину отрезка, соединяющего середины диагоналей трапеции
1) из $$\Delta ABD$$: $$MK=\frac{AD}{2}=9$$
2) из $$\Delta ABC$$: $$ML=\frac{BC}{2}=5$$
3) $$LK=MK-ML=4$$
Задание 18
Разобьем фигуру на трапецию и треугольник:
$$S_{1}=\frac{4+5}{2}*2=9$$ - площадь трапеции
$$S_{2}=\frac{1}{2}*3*5=7,5$$ - площадь треугольника
$$S=1_{1}+S_{2}=16,5$$ - общая площадь
Задание 19
В равнобедренном треугольнике ABC АВ = ВС, AС = 24, cos A = 0,48. Найдите площадь треугольника АВС.
Опустим высоту (медиану) BH
1) $$AH=\frac{AC}{2}=12$$
2) $$AB=\frac{AH}{\cos A}=\frac{12}{0,48}=25$$
3) По формуле Герона: $$S=\sqrt{p(p-a)(p-b)(p-c)}$$; $$p=\frac{a+b+c}{2}$$
$$p=\frac{25+25+24}{2}=37$$
$$S=\sqrt{37*12*12*13}=12\sqrt{481}$$
Задание 20
Какие из следующих утверждений верны?
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
- нет, противоположные равны
- нет, взаимоперпендикулярны и делятся пополам точкой пересечения .
- да.
Задание 21
Сократите дробь $$\frac{441^{n}}{7^{2n+1}*3^{2n-1}}$$
$$\frac{441^{n}}{7^{2n+1}*3^{2n-1}}=$$$$\frac{21^{2n}}{7^{2n+1}*3^{2n-1}}=$$$$\frac{7^{2n}*3^{2n}}{7^{2n+1}*3^{2n-1}}=$$$$7^{2n-(2n+1)}*3^{2n-(2n-1)}=$$$$7^{-1}*3^{1}=\frac{3}{7}$$
Задание 22
Иван шёл от дома до автобусной остановки пешком со скоростью 4 км/ч, затем ехал на автобусе до школы со скоростью 30 км/ч и затратил на весь путь 1 час. Обратно из школы он ехал на автобусе со скоростью 36 км/ч и шёл пешком от остановки до дома со скоростью 3 км/ч. На обратную дорогу он потратил 1 час 5 мин. Найти путь, который Иван проехал на автобусе, и расстояние от дома до остановки.
Пусть x км.-расстояние от дома до остановки , y км - от остановки до школы, тогда ( с учетом , что $$t=\frac{S}{v}$$):
$$\left\{\begin{matrix}\frac{x}{4}+\frac{y}{30}=1\\\frac{y}{36}+\frac{x}{3}=1\frac{5}{60}\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{x}{4}+\frac{y}{30}=1|*60\\\frac{y}{36}+\frac{x}{3}=\frac{13}{12}|*36\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}15x+2y=60\\y+12x=39\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}2y+15x=60\\2y+24x=78\end{matrix}\right.\Leftrightarrow$$ $$24x-15x=78-60\Leftrightarrow$$ $$x=2\Rightarrow$$ $$y+12*2=39\Leftrightarrow$$ $$y=15$$
Задание 23
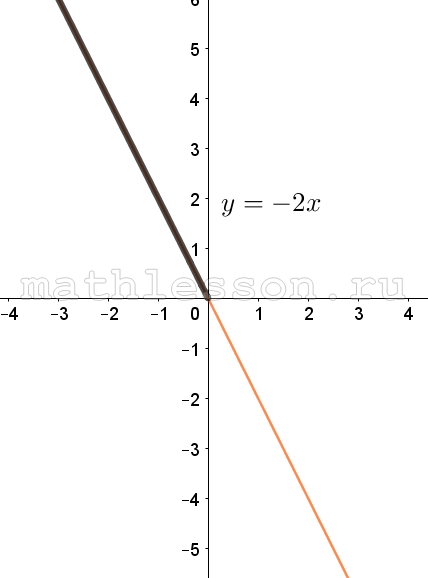
Постройте график функции $$y=\left\{\begin{matrix}-x^{2}-4x, x\geq 0\\-2x, x<0\end{matrix}\right.$$ и определите, при каких значениях m он имеет ровно две общие точки с прямой y=m.
Построим $$y=-x^{2}-4x$$. Вершина параболы: $$x_{0}=-\frac{-4}{-2}=-2$$, тогда $$y_{0}=-(-2)^{2}-4(-2)=4$$ (Черным выделена часть графика, с учетом $$x\geq 0$$):
Построим $$y=-2x$$ - это прямая, проходящая во второй и четвертой четвертях через начало координат (черным выделено с учетом условия $$x<0$$:
Объединим полученные кусочные функции:
С учетом того, что график функции $$y=m$$ - это прямая, параллельная оси Ох, то 2 точки пересечения с первоначальным графиком быть не может
Задание 24
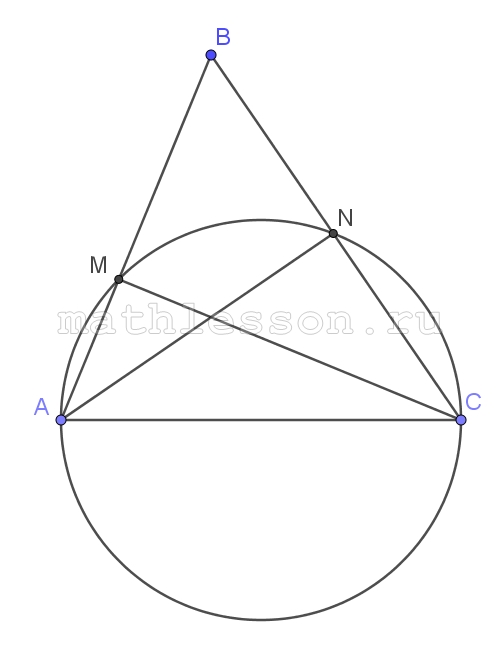
В треугольнике ABC на стороне AC как на диаметре построена окружность, которая пересекает сторону AB в точке M, а сторону BC – в точке N. Известно, что AC=2, AB=3, AM : MB = 2 : 3. Найдите AN..
1) $$AM :MB= 2: 3$$, $$AB=3$$$$\Rightarrow$$ $$AM=1,2$$, $$MB=1,8$$
2) $$\Delta AMC$$: $$MC=\sqrt{AC^{2}-AM^{2}}=1,6$$
3) $$\Delta MBC$$: $$BC=\sqrt{MB^{2}+MC^{2}}=\sqrt{5,8}$$
4) $$\Delta ABN\sim \Delta CMB$$ (оба прямоугольные ,$$\angle B$$ - общий )$$\Rightarrow$$ $$\frac{AN}{MC}=\frac{AB}{BC}$$$$\Rightarrow$$ $$AN=\frac{1,6*3}{\sqrt{5,8}}=\frac{4,8}{\sqrt{5,8}}$$
Задание 25
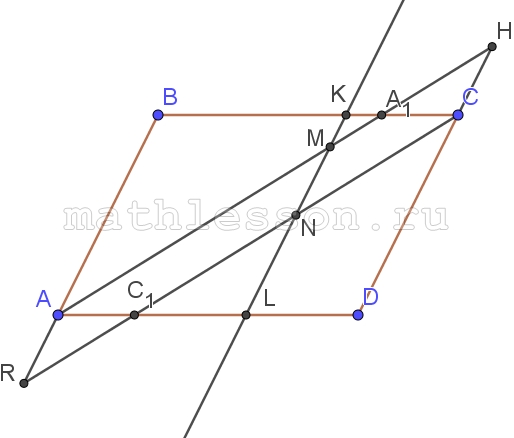
Дан параллелограмм ABCD. Прямая, параллельная AB, пересекает биссектрисы углов A и C в точках M и N соответственно. Докажите, что углы ADM и ABN равны
Биссектрисы $$AA_{1}$$ и $$CC_{1}$$; $$AA_{1}\cap CD=H$$; $$CC_{1}\cap AB=R$$
1) Пусть $$\angle A=2\alpha$$ $$\Rightarrow$$ $$\angle BAA_{1}=\angle A_{1}AD=$$$$\angle BCC_{1}=\angle C_{1}CD=\alpha $$($$AA_{1}; CC_{1}$$ - биссектрисы)
2) $$\angle AHC=\angle BAA_{1}=\alpha$$ ; $$\angle ARC=\angle C_{1}CR=\alpha$$ (накрест лежащие ) $$\Rightarrow$$ $$BC=AD$$, то равнобедренные $$\Delta RBC=\Delta AHD$$$$\Rightarrow$$ $$RB=AD(1)$$
3) $$\angle BAM=\angle BRN=\alpha$$ $$\Rightarrow$$ $$AM\left | \right |RN, AR\left | \right |NM$$ (по построению ) $$\Rightarrow$$ AMNR - параллелограмм $$\Rightarrow$$ $$RN=AM(2)$$
4)С учетом (1) и (2) , и, что $$\angle BRN =\angle MAD=\alpha$$ $$\Rightarrow$$ $$\Delta BRN=\Delta MAD$$$$\Rightarrow$$ $$\angle ABN=\angle ADM$$
Задание 26
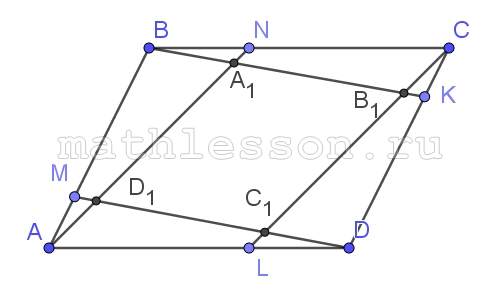
На сторонах AB, BC, CD и DA параллелограмма ABCD взяты соответственно точки M, N, K и L, причём AM : MB = CK : KD = 1/2 а BN : NC = DL : LA = 1/3. Найдите площадь четырёхугольника, вершины которого – пересечения отрезков AN, BK, CL и DM, если площадь параллелограмма ABCD равна 1
1) Введем обозначения, как показано на рисунке.
2) В силу равенства BLи AD и AB и CD, а так же, $$\frac{AM}{MB}=\frac{CK}{KD}$$ и $$\frac{BN}{NC}=\frac{DL}{AD}$$, получим равенство $$\Delta BKC$$ и $$\Delta AMD$$ ; $$\Delta ABN$$ и $$\Delta CDL$$, и что MBKD, ANCL - параллелограммы $$\Rightarrow$$ $$BK\left | \right |MD$$ и $$AN\left | \right |CL$$
3) Тогда по т. Фалеса $$\frac{BA_{1}}{BB_{1}}=\frac{BN}{BC}=\frac{1}{4}$$$$\Rightarrow$$, если $$S_{BNA_{1}}=y$$, то $$S_{BCB_{1}}=16y$$ (площади подобных относятся как квадрат коэффициента подобия)$$\Rightarrow$$ $$S_{NCB_{1}A_{1}}=15y$$. Аналогично, $$S_{DC_{1}L}=y$$; $$S_{AD_{1}C_{1}L}=15y$$
Если $$S_{AMD_{1}}=x$$ , то $$S_{ABA_{1}}=9x$$$$\Rightarrow$$ $$S_{MBA_{1}D_{1}}=8x$$
Аналогично, $$S_{CKB_{1}}=x$$; $$S_{B_{1}KDC_{1}}=8x$$ ,пусть $$S_{A_{1}B_{1}C_{1}D_{1}}=Z$$
4) $$S_{MBKD}=\frac{MB}{AB}*S_{ABCD}=\frac{2}{3}=2*8x+z$$
$$S_{ABCL}=\frac{NC}{BC}*S_{ABCD}=\frac{3}{4}=2*15y+z$$
$$S_{ABCD}=1=2*16y+2*9x+z$$
Получим :
$$\left\{\begin{matrix}16x+z=\frac{2}{3}\\30y+z=\frac{3}{4}\\32y+18x+z=1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{\frac{2}{3}-z}{16}\\y=\frac{\frac{3}{4}-z}{30}\\32(\frac{\frac{3}{4}-z}{30}+18(\frac{\frac{2}{3}-z}{16})+z=1|*120\end{matrix}\right.\Leftrightarrow$$$$8(12-16z)+15(6-9z)+120z=120\Leftrightarrow$$$$143z=66\Leftrightarrow$$$$z=\frac{6}{13}$$