ОГЭ математика 2019. Разбор варианта Алекса Ларина № 192.
Решаем ОГЭ 192 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №192 (alexlarin.com)
Решаем ОГЭ 192 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №192 (alexlarin.com)
Задание 1
Найдите значение выражения $$(1\frac{8}{15}-\frac{2}{15}):\frac{7}{15}$$
$$(1*\frac{8}{15}-\frac{2}{15}):\frac{7}{15}=$$$$(\frac{23}{15}-\frac{2}{15})*\frac{15}{7}=$$$$\frac{21}{15}*\frac{15}{7}=3$$
Задание 2
В нескольких эстафетах, которые проводились в школе, команды показали следующие результаты:
|
Команда |
I эстафета, мин. |
II эстафета, мин. |
III эстафета, мин. |
IV эстафета, мин. |
|
«Непобедимые» |
3,4 |
5,9 |
2,9 |
5,8 |
|
«Прорыв» |
4,5 |
4,3 |
3,2 |
5,4 |
|
«Чемпионы» |
4,9 |
4,8 |
2,7 |
6,3 |
|
«Тайфун» |
3,7 |
4,5 |
2,4 |
5,1 |
За каждую эстафету команда получает количество баллов, равное занятому в этой эстафете месту, затем баллы по всем эстафетам суммируются. Какое итоговое место заняла команда «Чемпионы», если победителем считается команда, набравшая наименьшее количество очков?
В ответе укажите номер правильного варианта.
Расставим места, которые заняли команды в каждой эстафете:
|
Команда |
I эстафета, мин. |
II эстафета, мин. |
III эстафета, мин. |
IV эстафета, мин. |
|
«Непобедимые» |
1 |
4 |
3 |
3 |
|
«Прорыв» |
3 |
1 |
4 |
2 |
|
«Чемпионы» |
4 |
3 |
2 |
4 |
|
«Тайфун» |
2 |
2 |
1 |
1 |
Тогда суммарные очки для каждой команды:
Задание 3
Между какими числами заключено число $$2\sqrt{5}$$
Варианты ответа
- 9 и 11
- 5 и 6
- 24 и 26
- 4 и 5
Представим $$2\sqrt{5}$$ в виде корня $$2\sqrt{5}=\sqrt{2^{2}*5}=\sqrt{20}$$. Очевидно что данное число располагается между $$\sqrt{16}$$ и $$\sqrt{25}$$ или 4 и 5, что соответствует 4 варианту.
Задание 4
Представьте выражение $$\frac{(c^{-3})^{-5}}{c^{-10}}$$ в виде степени с основанием c
Варианты ответа
- $$c^{-25}$$
- $$c^{-10}$$
- $$c^{-5}$$
- $$c^{-18}$$
$$\frac{(c^{-3})^{5}}{c^{-10}}=$$$$\frac{c^{-15}}{c^{10}}=$$$$c^{-15-{10}}=c^{-5}$$, что соответствует 3 варианту ответа
Задание 5
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Найдите разность между наименьшим и наибольшим значениями температуры. Ответ дайте в градусах Цельсия.
$$t_{min}=8$$ (между 21:00 и 00:00) $$t_{max}=24$$ (между 12:00 и 15:00) $$t_{min}-t_{max}=8-24=-16$$
Задание 6
Решите уравнение $$-2(x+1)-3(2-3x)=34$$
$$-2(x+1)-3(2-3x)=34$$ $$-2x-2-6+9x=34$$ $$7x=34+8=42$$ $$x=6$$
Задание 7
Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?
Частным лицам принадлежит : 100-60=40% Пусть x-сумма в млн.р. 40 млн.р.-100% X млн.р.-40% $$x=\frac{40*40}{100}=16$$ млн.р.
Задание 8
На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей. Какие из следующих утверждений неверны?
- пользователей из России больше, чем пользователей из Украины;
- больше трети пользователей сети — из Украины;
- пользователей из Беларуси больше, чем пользователей из Украины;
- пользователей из России больше 4 миллионов человек.
- пользователей из России больше, чем пользователей из Украины - верно
- больше трети пользователей сети — из Украины - неверно (сегмент меньше трети круга)
- пользователей из Беларуси больше, чем пользователей из Украины - неверно (сегмент Беларуси меньше)
- пользователей из России больше 4 миллионов человек - верно
Задание 9
На одной тарелке 12 пирожков, 4 из которых с капустой, а на другой тарелке 8 пирожков, 6 из которых с капустой. Из каждой тарелки взяли по одному пирожку. Какова вероятность того, что оба пирожка с капустой?
Вероятность взять с капустой из первой :$$P_{1}=\frac{4}{12}=\frac{1}{3}$$ Из второй :$$P_{2}=\frac{6}{8}=\frac{3}{4}$$ Общая вероятность $$P=P_{1}*P_{2}=$$$$\frac{1}{3}*\frac{3}{4}=0,25$$
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают.
ФОРМУЛЫ
- $$y=2x$$
- $$y=x^{2}-2$$
- $$y=\sqrt{x}$$
- $$y=-\frac{2}{x}$$
A-парабола $$(y=ax^{2}-b)\Rightarrow 2$$ Б-прямая $$(y=kx)\Rightarrow 1$$ B-гипербола $$(y=-\frac{k}{x})\Rightarrow 4$$
Задание 11
Укажите номер первого отрицательного члена арифметической прогрессии: 18; 15; …
Первый член прогресси: $$a_{1}=18$$, ее разность: $$d=a_{2}-a_{1}=15-18=-3$$
$$a_{n}a_{1}+d(n-1)=18-3(n-1)=21-3n<0\Leftrightarrow $$$$-3n<-21\Leftrightarrow n>7$$
Так как $$n \in N, n=8$$
Задание 12
Найдите значение выражения $$9b-\frac{3a-9b^{2}}{b}$$ при $$a=3\sqrt{2}, b=\sqrt{8}$$
$$9b+\frac{3a-9b^{2}}{b}=\frac{9b^{2}+3a-9b^{2}}{b}=$$$$\frac{3a}{b}=\frac{3+3\sqrt{2}}{\sqrt{8}}=$$$$\frac{9}{\sqrt{4}}=\frac{9}{2}=4,5$$
Задание 13
Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта позволяет формула $$F=1,8C+32$$ , где С — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 194по шкале Фаренгейта? Ответ округлите до десятых.
Выразим градусы Цельсия из формулы: $$F=1,8C+32\Leftrightarrow$$ $$1,8C=F-32\Leftrightarrow$$ $$C=\frac{F-32}{1,8}$$ Найдем значение: $$C=\frac{194-32}{1,8}=90$$
Задание 14
На каком рисунке изображено множество решений неравенства $$x^{2}-2x-3 \leq 0$$ Укажите неравенство, которое не имеет решений.
$$x^{2}-2x-3\leq 0\Leftrightarrow f(x)\leq 0$$
Пусть $$f(x)=0\Leftrightarrow x^{2}-2x-2=0$$ $$\left\{\begin{matrix}x_{1}+x_{2}=2\\x_{1}*x^{2}=-3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=3\\x_{2}=-1\end{matrix}\right.$$
Отметим точки на прямой ,расставим знаки f(x) на полученных промежутках.
Надо $$f(x) \leq 0\Leftrightarrow x \in [-1; 3]$$, что соответствует 1 варианту ответа
Задание 15
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,6 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 1,5 м. Найдите длину троса. Ответ дайте в метрах.
$$x=\sqrt{3,6^{2}+1,5^{2}}=$$$$\sqrt{\frac{1296+25}{100}}=$$$$\frac{39}{10}=3,9$$
Задание 16
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 42° и 78°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
$$\angle B=42+78=120$$
По свойству углов паралеллограма: $$\angle A=180-\angle B=180-120=60$$
Задание 18
Найдите площадь квадрата, если его диагональ равна 8.
Пусть AB=BC=a
По т. Пифагора $$\Delta ABC$$: $$a^{2}+a^{2}=8^{2}$$
$$2a^{2}=64$$
$$a^{2}=32$$
$$S_{ABCD}=a^{2}=32$$
Задание 19
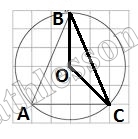
$$\angle BOC=\cup BC=135$$ $$\angle BAC=\frac{1}{2}\cup BC=\frac{135}{2}=67,5=\angle BCA$$ $$\angle ABC=180-67,5*2=45$$
Задание 20
Какие из следующих утверждений верны?
- Диагонали ромба равны.
- Площадь ромба равна половине произведения его диагоналей.
- Средняя линия трапеции равна половине основания трапеции.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
1.неверно (перпендикулярно и делятся пополам) 2.Верно 3.Неверно (полусумме оснований)
Задание 21
Решите систему уравнений $$\left\{\begin{matrix}x^{2}+xy+y^{2}=37\\ x^{3}-y^{3}=37\end{matrix}\right.$$
$$\left\{\begin{matrix}x^{2}+xy+y^{2}=37\\x^{3}-y^{3}=37\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x^{2}+xy+y^{2}=37\\(x-y)(x^{2}+xy+y^{2})=37\end{matrix}\right.$$ Поделим второе на первое уравнение :$$x-y=1\Leftrightarrow x=1+y$$ $$(1+y)^{2}+(1+y)y+y^{2}=37$$ $$1+2y+y^{2}+y+y^{2}+y^{2}=37$$ $$3y^{2}+3y-36=0|:3$$ $$y^{2}+y-12=0\Leftrightarrow$$ $$D=1+48=49\Leftrightarrow$$ $$\left\{\begin{matrix}y_{1}=\frac{-1+7}{2}=3\\y_{2}=\frac{-1-7}{2}=-4\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=1+3=4\\x_{2}=1-4=-3\end{matrix}\right.$$
Задание 22
Велосипедист проехал 25 км. При этом один час он ехал по ровной дороге, а один час – в гору. Какова скорость (в км/ч) велосипедиста по ровной дороге, если каждый километр по ровной дороге он проезжал на 2 минуты быстрее, чем в гору?
Пусть t-время 1 км по дороге , тогда $$t+\frac{2}{60}$$-время 1 км. в гору. Тогда $$v_{1}=\frac{1}{t}$$-скорость по дороге, $$v_{2}=\frac{1}{t+\frac{1}{30}}$$-скорость в гору. Тогда $$1*\frac{1}{t}+1*\frac{1}{t+\frac{1}{30}}=25$$
$$\frac{1}{t}+\frac{30}{30t+1}=25\Leftrightarrow$$ $$30t+1+30t=25(30t^{2}+t)$$
$$750t^{2}+25t-60t-1=0$$
$$750t^{2}-35t-1=0$$
$$D=1225+3000=65^{2}$$
$$t_{1}=\frac{35+65}{1500}=\frac{1}{15}$$
$$t_{2}<0$$
Тогда $$v_{1}=\frac{1}{\frac{1}{5}}=15$$
Задание 23
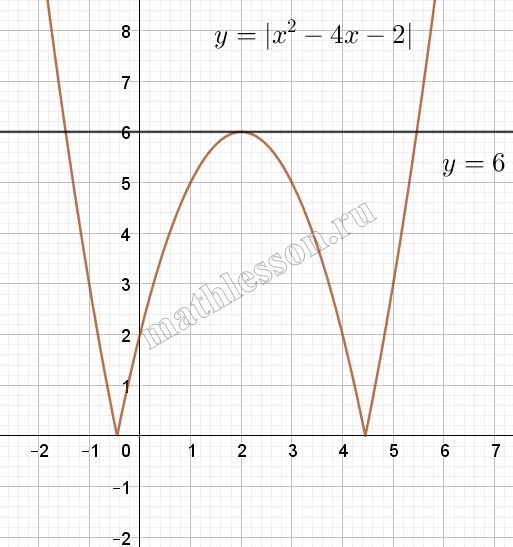
Постройте график функции $$y=|x^{2}-4x-2|$$ и определите, при каких значениях с прямая $$y=c$$ имеет с графиком три общие точки.
Данный график есть парабола $$y=x^{2}-4x-2$$, у которой часть ,которая располагается по Ox отображается симметрично Ox.
Найдем вершину параболы: $$x_{0}=-\frac{-4}{2}=2$$ $$y_{0}=\left | 4-8-2 \right |=6$$
$$y=c$$ - параллельна Ox, тогда при точки при y=6 , то есть c=6
Задание 24
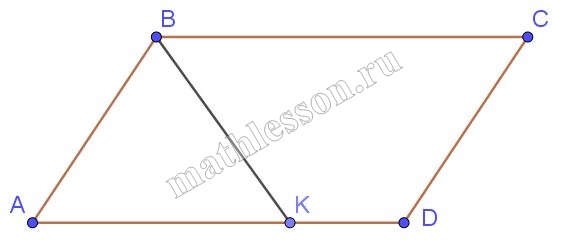
В параллелограмме ABCD биссектриса тупого угла B пересекает сторону АD в точке К. Найти периметр параллелограмма, если АВ = 12 и АК:КD = 4:3
a) Пусть $$K\in AD$$(внутри), тогда:
1) $$\angle ABK=\angle CBK$$(BK-биссектриса); $$\angle CBK=\angle AKB$$(накрест лежащие) $$\Rightarrow \Delta ABK$$-равнобедренный и $$AB = AK$$
2) пусть $$AB=4x =12\Rightarrow x=3, KD=3x=9$$$$\Rightarrow AD=21$$
3) $$P_{ABCD}=2(12+21)=66$$
b) вне AD. Аналогично $$AK=AB=12$$. Пусть $$DK=3x$$, тогда AK=4x и AD=x. Получаем $$4x=12\Rightarrow x=3$$ и $$P_{ABCD}=2(12+3)=30$$
Задание 25
На основаниях АВ и СD вне трапеции построены квадраты. Докажите, что прямая, соединяющая их центры, проходит через точку пересечения диагоналей трапеции.
Пусть $$K\in B_{1}C$$, $$O=BD\cap AC$$, $$M=KO\cap AD$$
1) $$\angle LCK=\angle MAN=45$$; $$\angle LCO=\angle OAN$$(накрест лежащие) $$\Rightarrow \angle KCA=\angle OAD_{1}\Rightarrow$$ $$CB_{1}\left | \right |AD_{1}$$
2) $$\angle LKC=\angle NMA$$(накрест лежащие) $$\Rightarrow \Delta KLC\sim \Delta ANM\Rightarrow$$ $$\frac{KC}{AM}=\frac{CL}{AN}=k$$
3) $$LC\left | \right |AN\Rightarrow$$ $$\Delta LCO\sim \Delta ONA\Rightarrow$$ $$\frac{LC}{AN}=\frac{LO}{ON}=k$$
4) $$LC\left | \right |AN \Rightarrow$$ $$\Delta BLO\sim \Delta OND\Rightarrow$$ $$\frac{LO}{ON}=\frac{BL}{ND}=k$$
5)т.к. $$\frac{LC}{AN}=k$$, $$\frac{BL}{ND}=k$$ $$\Rightarrow \frac{BC}{AD}=k$$,но $$\frac{KC}{AM}=k$$ и $$\angle KCL=\angle MAN\Rightarrow$$ $$\Delta KCB\sim \Delta ADC$$ и если K-центр , то и М-центр
Задание 26
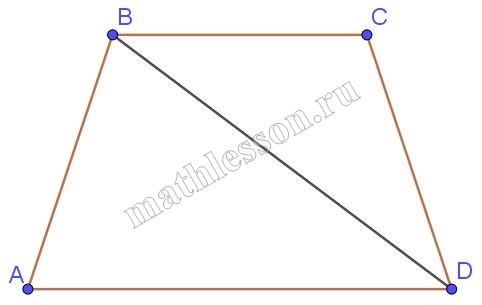
В равнобедренной трапеции ABCD длина боковой стороны АВ равна 2 и длина меньшего основания ВС равна 2. Найдите площадь трапеции, если $$BD\perp AB$$.
1) Пусть $$\angle DBC=\alpha$$ , тогда т.к. BC=CD, $$\angle BCD=\alpha$$, $$\angle C=180-2\alpha$$
2) По свойству углов трапеции $$\angle C+\angle D=180\Rightarrow$$ $$\angle D=180-(180-2\alpha )=2\alpha$$ $$\Rightarrow \angle BDA=\alpha$$
3) Пусть BD=y. Тогда из $$\Delta BCD$$:
$$CD^{2}=BC^{2}+AD^{2}-2BC*AD*\cos CBD$$
$$2^{2}=2^{2}+y^{2}-2*2*y*\cos \alpha \Leftrightarrow$$ $$y^{2}-4y*\cos \alpha =0$$
$$y(y-4\cos\alpha )=0$$, т.к. y-длина, то $$y\neq 0$$, тогда $$y-4\cos \alpha =0\Rightarrow y=4\cos\alpha$$
4) Из $$\Delta ABD$$:
$$\frac{AB}{BD}=tgBDA\Rightarrow$$ $$\frac{2}{4\cos\alpha }=tg\alpha =\frac{\sin\alpha }{\cos\alpha }\Leftrightarrow$$ $$\sin\alpha =\frac{1}{2}\Rightarrow$$ $$\alpha =30\Rightarrow$$ $$y=4*\frac{\sqrt{3}}{2}=2\sqrt{3}$$
5) $$S_{ABCD}=S_{BCD}+S_{ABD}=$$$$\frac{1}{2}*BC*BD*\sin CBD+\frac{1}{2}*AB*BD=$$$$\frac{1}{2}*2*2\sqrt{3}*\frac{1}{2}+\frac{1}{2}*2*2\sqrt{3}=$$$$\sqrt{3}+2\sqrt{3}=3\sqrt{3}$$