ОГЭ математика 2019. Разбор варианта Алекса Ларина № 195.
Решаем ОГЭ 195 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №195 (alexlarin.com)
Решаем ОГЭ 195 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №195 (alexlarin.com)
Задание 1
Найдите значение выражения $$\frac{1,5*3,2*10^{4}}{0,8*10^{5}}$$
$$\frac{1,5 *3,2*10^{4}}{0,8*10^{3}}=$$$$\frac{15*32*10^{2}}{8*10^{4}}=$$$$\frac{60}{10^{2}}=0,6$$
Задание 2
В таблице даны результаты забега девочек 9-го класса на дистанцию 30 м.
| Номер дорожки | 1 | 2 | 3 | 4 |
| Время (с) | 7,3 | 6,7 | 6,9 | 7,0 |
Зачёт выставляется, если показано время не хуже 6,8 с. Выпишите номера дорожек, по которым бежали девочки, получившие зачёт.
Не хуже, то есть меньше или равно. Тогда зачет получит только девочка со второй дорожки
Задание 3
На координатной прямой отмечено число a.
Какое из утверждений относительно этого числа является верным?
Варианты ответа
- 4 − a > 0
- 5 – a < 0
- а – 4 < 0
- a – 8 > 0
Пусть a=5,8. Проверим утверждения:
- $$4-a =4-5,8>0$$ - неверно
- $$5-a=5-5,8=-0,8<0$$ - верно
- $$a-4=5,8-4<0$$ - неверно
- $$a-8=5,8-8>0$$ - неверно
Задание 4
Какое из выражений равно степени $$7^{4-n}$$?
Варианты ответа
- $$\frac{7^{4}}{7^{n}}$$
- $$\frac{7^{4}}{7^{-n}}$$
- $$7^{4}-7^{n}$$
- $$(7^{4})^{-n}$$
$$7^{^4-n}=\frac{7^{4}}{7^{n}}$$, что соответствует 1 варианту
Задание 5
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее суточное количество осадков выпадало в Казани в данный период. Ответ дайте в миллиметрах.
15 числа выпало 6 миллиметров
Задание 6
Решите уравнение $$(x+15)^{2}=(x-11)^{2}$$
$$(x+15)^{2}=(x-11)^{2}\Leftrightarrow$$$$(x+15)^{2}-(x-11)^{2}=0\Leftrightarrow$$$$(x+15-x+11)(x+15+x-11)=0\Leftrightarrow$$$$26(2x+4)=0 2x=4=0\Leftrightarrow x=-2$$
Задание 7
Брюки стоят 2450 рублей, а пиджак – 3185 рублей. На сколько процентов пиджак дороже, чем брюки?
Пусть стоимость брюк -100% , тогда:
$$x=\frac{3185*100}{2450}=130$$ % составляет стоимость пиджака относительно стоимости брюк
130-100=30% - разница в процентах
Задание 8
На диаграмме показаны религиозные составы населения Германии, США, Австрии и Великобритании. Определите по диаграмме, в каких странах суммарная доля протестантов и католиков превышает 75%.
Варианты ответа:
Только в Австрии количество католиков и протестантов составляет более 75 процентов.
Задание 9
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,09. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Вероятность того, что пишет хорошо: $$P=1-0,09=0,91$$ (как противоположное событие)
Задание 10
Найдите значение с по графику функции $$y=ax^{2}+bx+c$$ , изображенному на рисунке.
Варианты ответа
- -3
- 1
- 2
- 3
Коэффициент c равен значению ординаты точки пересечения графика функции и оси Oy $$\Rightarrow c=3$$, что соответствует 4 варианту ответа
Задание 11
Дана арифметическая прогрессия: 30; 23; 16; … . Найдите первый отрицательный член этой прогрессии.
Найдем разность данной прогрессии: $$d=a_{n+1}-a_{n}=23-30=-7$$
Тогда $$a_{n}=a_{1}+d(n-1)=30-7(n-1)=37-7n<0\Leftrightarrow$$ $$-7n<-3,7\Leftrightarrow$$ $$n>\frac{37}{7}$$.
С учетом, что $$n \in N$$, $$n=6$$, тогда $$a_{6}=30-7(6-1)=-5$$
Задание 12
Найдите значение выражения $$20ab-5(-2a-b)^{2}$$ при $$a=\sqrt{5}, b=\sqrt{6}$$
$$20ab-5(-2a-b)^{2}=$$$$20ab-5(4a^{2}+4ab+b^{2})=$$$$-5(4(\sqrt{5})^{2}+(\sqrt{5})^{2})$$$$=-5(20+6)=-130$$
Задание 13
Закон Джоуля–Ленца можно записать в виде Q=I2Rt, где Q — количество теплоты (в джоулях), I — сила тока (в амперах), R — сопротивление цепи (в омах), а t — время (в секундах). Пользуясь этой формулой, найдите время t (в секундах), если Q=378 Дж, I=3 A, R=7 Ом.
Задание 14
При каких значениях a выражение 12 – 0,3a принимает положительные значения?
Варианты ответа
- a > 40
- a < 40
- a < − 40
- a > − 40
$$12-0,3a>0\Leftrightarrow$$ $$-0,3a>-12\Leftrightarrow$$$$a<40$$, что соответствует 2 варианту ответа
Задание 15
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота средней опоры 2,2 м, высота большей опоры 2,5 м. Найдите высоту меньшей опоры. Ответ дайте в метрах
Пусть x – высота меньшей, тогда $$\frac{x+2,5}{2}=2,2\Leftrightarrow$$ $$x+2,5=4,4\Leftrightarrow$$ $$x=1,9$$
Задание 16
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 35. Найдите величину угла MOK. Ответ дайте в градусах
$$\angle OKM=\angle OMK$$($$\Delta OMK$$ - равнобедренный ) $$\angle OKM=90-35=55$$ $$\angle MOK=180-2*55=70$$
Задание 17
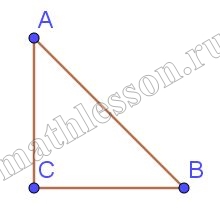
Катеты прямоугольного треугольника равны 24 и 7. Найдите высоту, проведённую к гипотенузе.
Пусть c-гипотенуза, h-высота $$c=\sqrt{24^{2}+7^{2}}=25$$ (по т. Пифагора) $$h=\frac{24*7}{25}=6,72$$
Задание 18
$$S=\frac{3+7}{2}*4=20$$ клеток Площадь клетки: $$5*5=25$$ Итоговая площадь $$20*25=500$$
Задание 19
Площадь прямоугольного треугольника равна $$49\sqrt{12}$$ . Один из острых углов равен 30°. Найдите длину гипотенузы треугольника.
Пусть x-гипотенуза AB, тогда $$AC=\frac{x}{2}$$
$$S=\frac{1}{2}*AB*AC*\sin A=49\sqrt{12}\Leftrightarrow$$$$\frac{1}{2}*x*\frac{x}{2}*\frac{\sqrt{3}}{2}=49\Leftrightarrow$$$$\sqrt{12} x^{2}=49*2*2^{3}\Leftrightarrow$$ $$x=7*4=28$$
Задание 20
Какие из следующих утверждений верны?
- Площадь трапеции равна произведению средней линии на высоту.
- Площадь параллелограмма равна произведению его сторон.
- Площадь квадрата равна произведению его диагоналей.
- Верно
- Неверно(на синус угла между ними)
- Неверно( половине произведения)
Правильным ответом будет вариант под номером 1
Задание 21
Найдите значение выражения: $$\sqrt{21+8\sqrt{5}}-\sqrt{21-8\sqrt{5}}$$
Выделим полные квадраты под корнем (чтобы восользоваться формулой $$\sqrt{a^{2}}=|a|$$:
Пусть $$\left\{\begin{matrix} a^{2}+b^{2}=21\\ 2ab=8\sqrt{5}\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix} a^{2}+b^{2}=21\\ab=4\sqrt{5}\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix} a=4\\b=\sqrt{5}\end{matrix}\right.$$
Тогда: $$\sqrt{(4+\sqrt{5})^{2}}-\sqrt{(4-\sqrt{5})^{2}}=$$$$\left | 4+\sqrt{5} \right |-\left | 4-\sqrt{5} \right |=$$$$4+\sqrt{5}-4+\sqrt{5}=2\sqrt{5}$$ (учитываем знак подмодульного выражения (если положительное, то раскрываем модуль не меняя знаки, если отрицательное - то меняем) при раскрытии модуля)
Задание 22
Моторная лодка спускается вниз по реке от А до В за 6 часов, причем собственная скорость лодки в три раза больше скорости течения реки. За какое время лодка поднимется вверх по реке от В до А.
Пусть x - собственная скорость лодки (в частях расстояния в час), y - течения . Пусть расстояние равно 1. Тогда : $$\frac{1}{x+y}=6$$
При этом $$x=3y\Rightarrow \frac{1}{3y+y}=6\Leftrightarrow$$ $$\frac{1}{4y}=6\Leftrightarrow$$ $$y=\frac{1}{24}$$ частей расстояния в час
Тогда время вверх по течению: $$\frac{1}{3y-y}=\frac{1}{2y}=\frac{1}{2*\frac{1}{24}}=12$$ часов
Задание 23
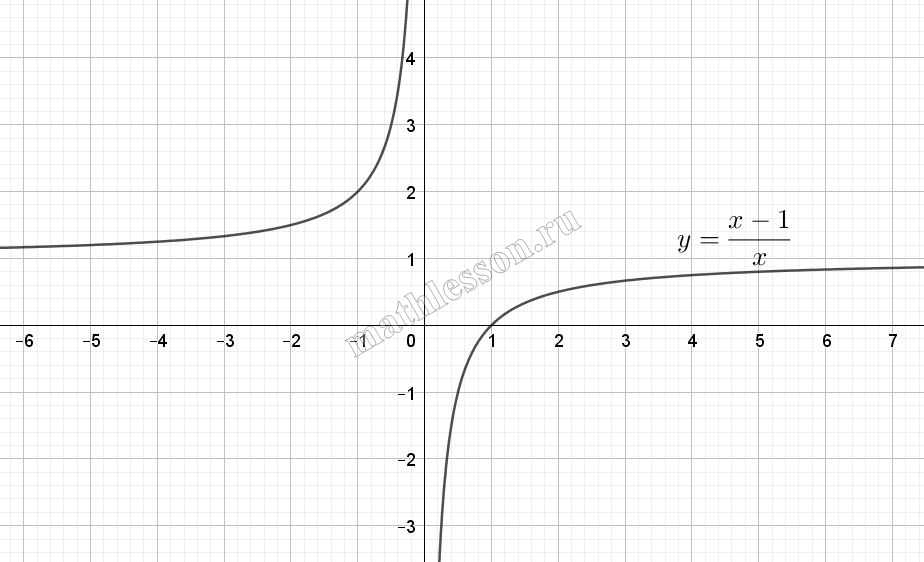
Постройте график функции $$y=|\frac{x-1}{x}|$$ и определите, при каких значениях а прямая y=ах имеет с графиком ровно две общие точки.
Преобразуем правую часть функции: $$y=\left | \frac{x-1}{x} \right |=\left | 1-\frac{1}{x} \right |$$. То есть у нас дан график функции $$y=\frac{1}{x}$$, смещенный на 1 вверх по оси Оу и отображенный относительно оси Оу.
Кроме того, наличие модуля отобрадает ту часть графика, которая находится под осью Ох (показана на рисунке), симметрично относительно Ох:
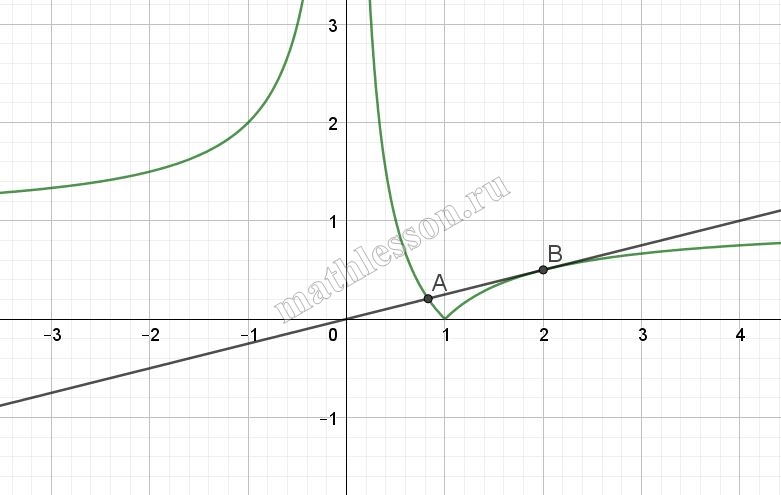
Итоговый график функции будет выглядить, как:
Необходимо найти такое значение а, при котором будет ровно два решения. В таком случае график прямой должен касаться графика исходной функции (точка B):
Так как касается в той части графика, где функции (с учетом раскрытия модуля) выглядит как $$y=1-\frac{1}{x}$$. Так как там касается, то должна быть одна точка пересечения с данным графиком: $$ax=1-\frac{1}{x}\Leftrightarrow$$$$\frac{ax^{2}-x+1}{x}=0$$ При этом $$D=1-4a=0\Leftrightarrow$$$$a=\frac{1}{4}=0,25$$
Задание 24
В равнобедренной трапеции с основаниями 10 и 26 см диагональ является биссектрисой острого угла. Найдите площадь трапеции.
1) $$\angle BAC=\angle CAD$$ (AC-бисссектриса), $$\angle CAD=\angle BCA$$ ( накрест лежащие ), тогда $$\angle BAC=\angle ACA$$, следовательно, $$\Delta ABC$$ - равнобедренный, и AB=BC=10
2) Пусть BH=CM - высота, тогда $$AH=MD=\frac{AD-BC}{2}=8$$
3) из $$\Delta ABH:$$ $$BH=\sqrt{AB^{2}-AB^{2}}=6$$
4) $$S_{ABCD}=\frac{10+26}{2}*6=108$$
Задание 25
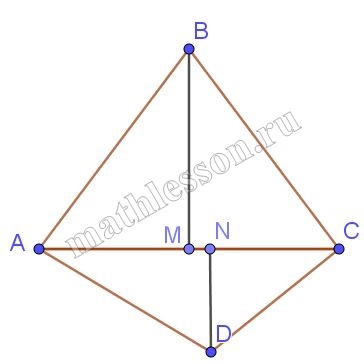
В выпуклом четырёхугольнике ABCD противоположные углы А и С прямые. На диагональ АС опущены перпендикуляры ВМ и DN. Докажите, что СМ = NA.
1) Пусть $$\angle ABM=\alpha$$, тогда из $$\Delta ABM: \angle BAM=90-\alpha$$ , тогда $$\angle MAD=\alpha$$ и из $$\Delta ADH:$$$$\angle ADN =90-\alpha \Rightarrow$$ $$\Delta ABM\sim \Delta AND$$, тогда : $$\frac{DH}{AM}=\frac{AN}{BM}\Rightarrow$$ $$DN*BM=AM*AN(1)$$
2) Аналогично $$\Delta BMC\sim \Delta CHD$$ и $$\frac{DH}{CM}=\frac{NC}{BM}\Rightarrow$$ $$DN*BM=CM*NC(2)$$
3) С учетом (1) и (2): $$AM *AN=CM*NC$$ или $$AM(AM+MN)=CN(CN+MN)\Leftrightarrow$$ $$AM^{2}+AM*MN=CN^{2}+CN*MN\Leftrightarrow$$ $$AM^{2}-CN^{2}+AM*MN-CN*MN=0\Leftrightarrow$$ $$(AM-CN)(AM+CN)+MN(AM-CN)=0\Leftrightarrow$$ $$(AM-CN)(AM+CN+MN)=0$$. $$AM+CN+MN>0$$ всегда, следовательно, $$AM-CN=0$$ или $$AM=CN$$
Задание 26
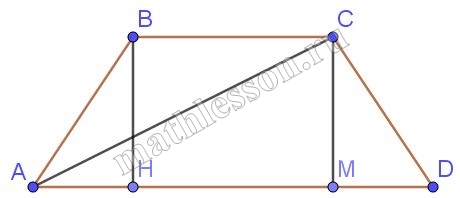
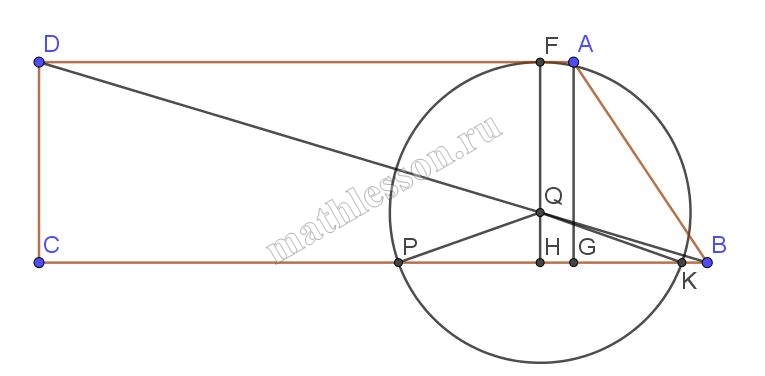
На диагонали BD прямоугольной трапеции ABCD ($$\angle D=90^{\circ}$$, ВС ॥ AD) взята точка Q так, что BQ : QD = 1 : 3. Окружность с центром в точке Q касается прямой AD и пересекает прямую ВС в точках Р и К. Найдите длину стороны АВ, если ВС = 9, AD = 8, РК = 4
1) Пусть F точка касания и $$CD=x$$. Опустим перпендикуляры FH(через Q) и $$AC_{1}$$. Тогда $$CD=FH=AC_{1}=x$$
2) $$\Delta QHB\sim \Delta DCB$$: $$\frac{CD}{QH}=\frac{BD}{BQ}\Rightarrow$$ $$QH=\frac{1}{4}EB=\frac{1}{4}x\Rightarrow$$$$FQ=x-\frac{1}{4}x=\frac{3}{4}x$$. Но QP=QF (радиус)
3) из $$\Delta QHP:$$ $$PH=\frac{1}{2}PK=2$$. Тогда по т. Пифагора : $$PQ^{2}=QH^{2}+PH^{2}\Leftrightarrow$$ $$(\frac{3}{4}x)^{2}=(\frac{1}{4}x)^{2}+2^{2}\Leftrightarrow$$ $$\frac{x^{2}}{2}=4\Rightarrow$$ $$x^{2}=8$$
4)из $$\Delta AC_{1}B$$ : $$AB=\sqrt{AC_{1}^{2}+C_{1}B^{2}}$$. $$C_{1}B=CB-AD=9-8=1$$, $$AC_{1}^{2}=x^{2}=8$$, тогда $$AB=\sqrt{8+1}=3$$