ОГЭ математика 2022. Разбор варианта Алекса Ларина № 293.
Больше разборов на моем ютуб-канале
Задания 1-5
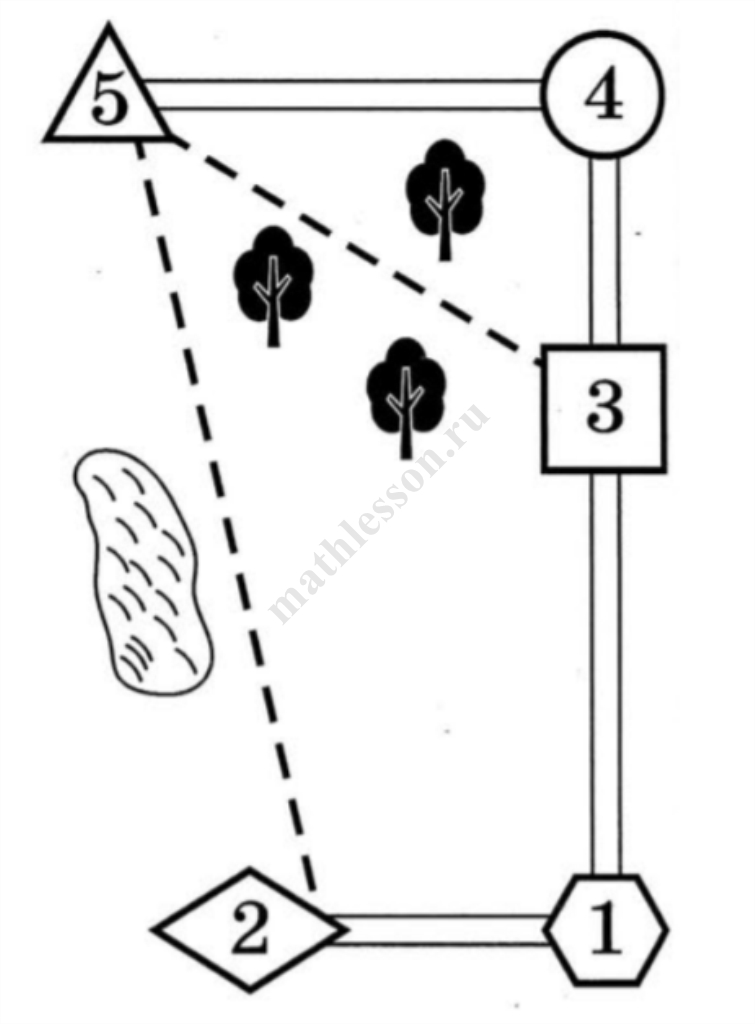
Юра летом отдыхает у дедушки и бабушки в деревне Казаково. Юра с дедушкой собираются съездить на велосипедах в село Бор на железнодорожную станцию. Из Казаково в Бор можно проехать по шоссе до деревни Заулки, где нужно свернуть под прямым углом направо на другое шоссе, ведущее в Бор через посёлок Малахово. Из Казаково в Бор можно проехать через посёлок Малахово и не заезжая в Заулки, но тогда первую часть пути надо проехать по прямой лесной дорожке. Есть и третий маршрут: доехать по прямой тропинке мимо пруда до села Шокша и там, повернув налево, по шоссе добраться до Бора.
По шоссе Юра с дедушкой едут со скоростью 15 км/ч, а по лесной дорожке и тропинке – 12 км/ч. Расстояние по шоссе от Казаково до Заулок равно 24 км, от Бора до Заулок – 30 км, от Бора до Малахово – 20 км, а от Бора до Шокши – 8 км.
Дороги из Шокши в Бор и из Малахово в Бор пересекаются под прямым углом.
1. Пользуясь описанием, определите, каким цифрами на плане обозначены населённые пункты. Заполните таблицу. В ответе запишите последовательность пяти цифр без пробелов, запятых и других разделительных символов.
| Населённые пункты | с. Бор | д. Заулки | д. Казакова | п. Малахово | с. Шокша |
| Цифры |
2. Сколько километров проедут Юра с дедушкой, если они поедут на станцию по шоссе через Заулки?
3. На сколько процентов скорость, с которой едут Юра с дедушкой по тропинке, меньше их скорости по шоссе?
4. Найдите расстояние (в км) от деревни Казаково до села Шокша по прямой тропинке.
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Юра с дедушкой, если поедут этим маршрутом.
Задание 11
На рисунке изображён график функции $$y=ax^{2}+bx+c$$. Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. В ответе укажите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.
| утверждения | промежутки |
| А) функция убывает на промежутке | $$-\frac{\sqrt{5}+1}{2};\frac{\sqrt{5}-1}{2}$$ |
| Б) функция возрастает на промежутке | $$(-\infty;-\frac{\sqrt{5}+1}{2}];[\frac{\sqrt{5}-1}{2};+\infty)$$ |
| В) функция неотрицательна на промежутке | $$(-\infty;-0,5]$$ |
| Г) функция неположительна на промежутке | $$[-0,5;+\infty)$$ |
Задание 14
Лене надо подписать 972 открытки. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Лена подписала 20 открыток. Определите, сколько открыток было подписано за седьмой день, если вся работа была выполнена за 18 дней.
Задание 19
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.
- Диагонали параллелограмма равны.
- Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
- Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.