ЕГЭ Профиль
Задание 4697
Две окружности с центрами O1 и O2 пересекаются в точках A и B, причём точки O1 и O2 лежат по разные стороны от прямой AB. Продолжения диаметра CA первой окружности и хорды CB этой окружности пересекают вторую окружности в точках D и E соответственно.
Задание 4699
Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что $$\sin \angle AOC = \frac{\sqrt{15}}{4}$$ Прямые PC и AQ пересекаются в точке K. Найдите отношение QK : KA
Задание 4701
В трапеции АBCD угол BAD прямой. Окружность, построенная на большем основании АD как на диаметре, пересекает меньшее основание BC в точке C и M.
а) Докажите, что угол BАM равен углу CАD.
б) Диагонали трапеции АBCD пересекаются в точке O. Найдите площадь треугольника АOB, если АB = 6, а BC = 4BM.
Задание 4774
В треугольнике АВС точка D есть середина АВ, точка Е лежит на стороне ВС, причем $$BE=\frac{1}{3}AC$$ . Отрезки АЕ и CD пересекаются в точке О.
Задание 4865
Задание 4916
АК ‐ биссектриса треугольника АВС, причем ВК:КС=2:7. Из точек В и К проведены параллельные прямые, которые пересекают сторону АС в точках D и F соответственно, причем AD:FC=3:14
Задание 5011
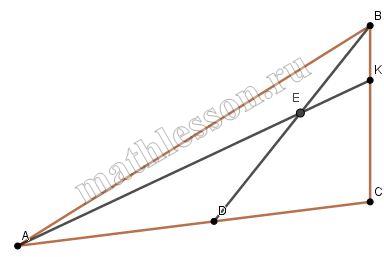
На стороне ВС треугольника АВС отмечена точка К. Оказалось, что отрезок АК пересекает медиану ВD в точке Е так, что АЕ=ВС.
а) 1) По т. Менелая: $$\frac{AE}{EK}\cdot\frac{BK}{BC}\cdot\frac{CD}{DA}=1$$; $$AE=BC$$; $$CD=DA$$ $$\Rightarrow$$ $$\frac{BK}{EK}\cdot\frac{1}{1}\cdot\frac{1}{1}=1$$ $$\Rightarrow$$ $$BK=EK$$
ч.т.д.
б) 1) Пусть $$BK=EK=x$$; $$AK=7+x$$; $$KC=7-x$$; $$AC=8$$
$$\bigtriangleup ABC$$: $$\cos C=\frac{AC^{2}+BC^{2}-AB^{2}}{2AC\cdot BC}=\frac{64+49-169}{2\cdot8\cdot7}=-\frac{1}{2}$$ $$\Rightarrow$$ $$\angle C=120^{\circ}$$; $$\bigtriangleup AKC$$: $$AK^{2}=AC^{2}+KC^{2}-2AC\cdot KC\cdot\cos C$$ $$\Leftrightarrow$$ $$(7+x)^{2}=8^{2}+(7-x)^{2}-2\cdot8\cdot(7-x)(-\frac{1}{2})$$; $$49+14x+x^{2}=64+49-14x+x^{2}+56-8x$$; $$36x=120$$ $$\Leftrightarrow$$ $$x=\frac{120}{36}=\frac{10}{3}$$ $$\Rightarrow$$ $$KC=7-\frac{10}{3}=\frac{11}{3}$$;
2) По т. Менелая: $$\frac{BE}{ED}\cdot\frac{AD}{AC}\cdot\frac{CK}{KB}=1$$; $$\frac{BE}{ED}\cdot\frac{4}{8}\cdot\frac{11}{3}\cdot\frac{3}{10}=1$$; $$\frac{BE}{ED}=\frac{20}{11}$$ $$\Rightarrow$$ $$\frac{BE}{ED}=\frac{20}{31}$$
3) $$\frac{S_{BEK}}{S_{BDC}}=\frac{BE\cdot BK}{BD\cdot BC}=\frac{20}{31}\cdot\frac{10}{3\cdot7}=\frac{200}{651}$$ $$\Rightarrow$$ $$S_{BEK}=\frac{200}{651}S_{BDC}$$ $$\Rightarrow$$ $$S_{DEKC}=\frac{451}{651}S_{BDC}$$;
4) $$S_{BDC}=\frac{1}{2}S_{ABC}=\frac{1}{2}\cdot\frac{1}{2}\cdot8\cdot7\cdot\frac{\sqrt{3}}{2}=7\sqrt{3}$$; $$S_{DEKC}=\frac{451\cdot7\sqrt{3}}{651}=\frac{451\sqrt{3}}{93}$$
Задание 5059
Дана трапеция ABCD с основаниями AD и ВС. Диагонали АС и BD пересекаются в точке О, а прямые АВ и CD – в точке К. Прямая КО пересекает стороны ВС и AD в точках М и N соответственно, и угол BAD равен $$30^{\circ}$$. Известно, что в трапеции ABMN и NMCD можно вписать окружность.
А) 1) $$AB\cap DC=K$$; $$AC\cap DB=O$$. По замечательному свойству трапеции середины AD и BC лежат на прямой $$KO\Rightarrow$$ M и N – середины BC и AD. По условию в трапеции ABMN и NMCD можно вписать окружность $$\Rightarrow$$ $$\left\{\begin{matrix}BM+AN=AB+MN\\MC+ND=CD+MN\end{matrix}\right.$$. А так как BM=MC, AC=ND, AB=CD, ABCD -равнобедренная трапеция. Тогда $$\Delta AKD$$ - равнобедренный и $$\angle AKD=120$$ - тупой угол
Б) 1) Пусть AD=a, BC=b; $$\frac{S_{AKD}}{S_{BKC}}=(\frac{a}{b})^{2}\Rightarrow$$ $$S_{AKD}=(\frac{a}{b})^{2}S_{BKC}$$; $$S_{ABCD}=S_{AKD}-S_{BKC}=(\frac{a}{b})^{2}S_{BKC}=((\frac{a}{b})^{2}-1)S_{BKC}$$. Тогда $$\frac{S_{BKC}}{S_{ABCD}}=\frac{1}{(\frac{a}{b})^{2}-1}$$
2) $$AB+MN=BM+AN=\frac{a+b}{2}$$;$$MN=BF=\frac{1}{2}AB$$, т.к. $$MN\perp AD \angle BAD=30\Rightarrow$$ $$\frac{3}{2}AB=\frac{a+b}{2}$$, откуда $$AB=\frac{a+b}{3}$$.
3) С другой стороны $$AB=\frac{AF}{\cos 30}=\frac{a-b}{2}:\frac{\sqrt{3}}{2}=\frac{a-b}{\sqrt{3}}$$
4) Тогда $$\frac{a+b}{3}=\frac{a-b}{\sqrt{3}}$$, откуда найдем $$\frac{a}{b}=\frac{\sqrt{3}+1}{\sqrt{3}-1}$$
5) $$\frac{S_{BKC}}{S_{ABCD}}=\frac{1}{(\frac{\sqrt{3}+1}{\sqrt{3}-1})^{2}-1}=$$$$\frac{(\sqrt{3-1})^{2}}{(\sqrt{3}+1)^{2}-(\sqrt{3}-1)^{2}}=$$$$\frac{4-2\sqrt{3}}{2*2\sqrt{3}}=$$$$\frac{2-\sqrt{3}}{2\sqrt{3}}=\frac{2\sqrt{3}-3}{6}$$
Задание 6043
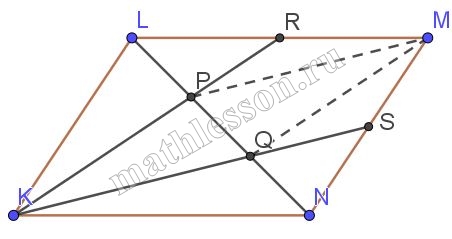
На диагонали LN параллелограмма KLMN отмены точки Р и Q, причем LP=PQ=QN
а)1) Построим MQ:NQ=PL;
$$NM=KL \angle QLM=\angle KLP\Rightarrow \Delta KLP=\Delta QMN$$ и $$MQ=KP$$
2)Аналогично, построим MP из равенства $$\Delta LMP$$ и $$\Delta KQN$$ MP=KQ;
3)из п.1 и п.2= KPMQ-паралелограмм $$\Rightarrow MP\left | \right |KQ$$,тогда по т. Фалеса т.к. PQ=QN, то MS=SN , аналогично : $$\angle P=PQ$$, тогда $$\angle R=RM$$;
б )1) Пусть $$S_{KLMN}=S$$,тогда $$S_{MLN}=\frac{1}{2}*S$$.
2) $$\frac{S_{RLP}}{S_{MLN}}=\frac{RL*LP}{ML*LN}=$$$$\frac{\frac{1}{2}*ML*\frac{1}{3}*LN}{ML*LN}=$$$$\frac{1}{6}\Rightarrow S_{RLP}=\frac{1}{6}*S_{MLN}$$.
3)Аналогично п2: $$S_{QNS}=\frac{1}{6}*S_{MNL}\Rightarrow S_{MRPQS}=S_{MLN}-2*\frac{1}{6}*S_{MNK}=$$$$\frac{2}{3}*S_{MKN}=\frac{1}{2}*\frac{2}{3}*S=\frac{1}{3}*S$$.
4)$$\frac{S_{KLMN}}{S_{MRPQS}}=\frac{1}{3}*S=\frac{3}{1}$$