Показательные функции

Скрыть

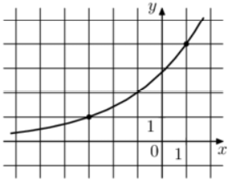
Точки $$A(0;-4)$$ и $$B(1;-2)$$ принадлежат графику функции, тогда:

$$\left\{\begin{matrix} -4=a^0+b\\ -2=a^1+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -4=1+b\\ -2=a+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=-5\\ a=-2+5=3 \end{matrix}\right.$$

Тогда:

$$f(4)=3^4-5=81-5=76$$

Скрыть

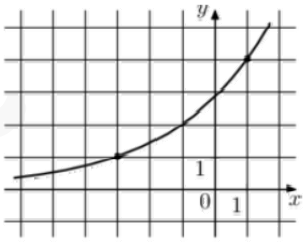
Точки A(0;2) и B(-1;3) принадлежат графику функции. Получили:

$$\left\{\begin{matrix} 2=a^0+b\\ 3=a^{-1}+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 2=1+b\\ a^{-1}=3-b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=1\\ a^{-1}=2 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=1\\ a=\frac{1}{2} \end{matrix}\right.$$

Получили:

$$(\frac{1}{2})^x+1=33\Leftrightarrow(\frac{1}{2})^x=32=(\frac{1}{2})^{-5}\Leftrightarrow x=-5$$

Скрыть

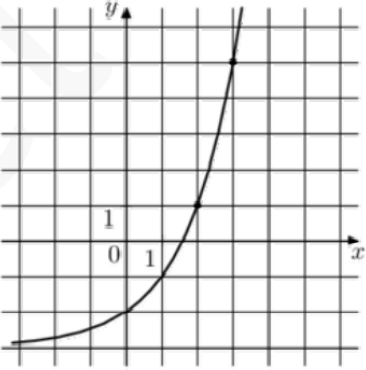
Точки $$(1;3)$$ и $$(2;1)$$ принадлежат графику функции $$f(x).$$ Тогда:

$$\left\{\begin{matrix} 3=a^{1+b}\\ 1=a^{2+b} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 3=\frac{a^{1+b}}{a^{2+b}}=a^{-1}\\ a^{2+b}=1 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=\frac{1}{3}\\ (\frac{1}{3})^{2+b}=1 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=\frac{1}{3}\\ b=-2 \end{matrix}\right.$$

Получили:

$$f(x)=(\frac{1}{3})^{x-2}$$

Тогда:

$$f(-1)=(\frac{1}{3})^{-1-2}=(\frac{1}{3})^{-3}=27$$

Скрыть

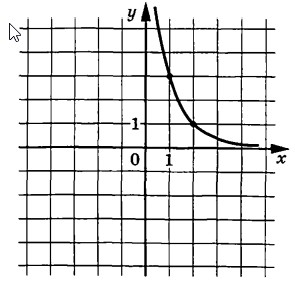
Точки $$(-2;1)$$ и $$(0;2)$$ принадлежат графику $$f(x).$$ Тогда:

$$\left\{\begin{matrix} 1=a^{-2+b}\\ 2=a^{0+b} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 2=a^{b-(b-2)}\\ 2=a^b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a^2=2\\ a^b=2 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=\sqrt{2}\\ b=2 \end{matrix}\right.$$

Получили:

$$f(x)=(\sqrt{2})^{x+2}$$

Тогда:

$$(\sqrt{2})^{x+2}=8$$

$$x+2=6$$

$$x=4$$

Скрыть

$$4=a^{1+b}​$$

$$​1=a^{-3+b}$$​

Откуда, логарифмируя, можно получить ​$$b=3​$$

​$$4=a^4$$​ пока так и оставим

$$​f(−7)=a^{−4}=\frac{1}{a^4}=\frac{1}{4}=0,25$$

Скрыть Из рисунка видно, какие точки лучше всего взять

$$​1=a^{−3+b}​$$

$$​4=a^{1+b}$$​

Можно по-разному решать, один из способов прологарифмировать и поделить одно на другое, выразить ​$$b$$​

Другой способ это умножить первое на 4 и вычесть одно из другого, откуда можно легко выразить $$a$$​

$$​f(x)=(\sqrt{2})^{x+3​}$$

$$​f(-7)=0,25$$

Скрыть

Из рисунка видно, какие точки удобнее всего взять

​$$1=a^2+b​$$

​$$5=a^3+b​$$

Вычтем одно из другого

$$​a^3−a^2=4​$$

$$​a(a^2−a)=4​$$, очевидно, что ​$$a=2​$$

Значит, $$​b=3$$

$$​f(x)=2^x−3​$$

​$$f(6)=61$$

Скрыть

Скрыть

Скрыть

Скрыть

Скрыть

Скрыть

Скрыть

Скрыть

Скрыть