ЕГЭ Профиль
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1098
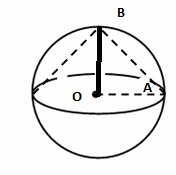
В шар вписан конус так, что центр основания конуса совпадает с центром шара. Найдите площадь боковой поверхности конуса, если известно, что площадь поверхности шара равна $$10\sqrt{2}$$

Ответ: 5
Скрыть
Площадь поверхности шара: $$S_1=4\pi R^{2}$$
Площадь боковой поверхности конуса: $$S=\pi R*l$$, где R - радиус шара, а в нашем случае и основания конуса, а l - образующая конуса
OA=OB=R
Значит $$BA = \sqrt{OA^{2}+OB^{2}}=R\sqrt{2}$$. То есть $$l=R\sqrt{2}$$.
Значит площадь боковой поверхности конуса:
$$S=\pi R*R\sqrt{2}=\pi R^{2}\sqrt{2}=\frac{S_{1}\sqrt{2}}{4}=$$
$$\frac{S_{1}\sqrt{2}}{4}=\frac{10*\sqrt{2}\sqrt{2}}{4}=5$$
Задание 2493
Площадь основания конуса равна $$16\pi $$, высота – 6. Найдите площадь осевого сечения конуса.
Ответ: 24
Скрыть
Sосн$$=16\pi=\pi R^{2}\Rightarrow R^{2}=16$$ $$\Rightarrow R=4$$
Sсечен$$=\frac{1}{2}\cdot 8\cdot 6=24$$
Задание 3112
Площадь боковой поверхности конуса равна 60. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь боковой поверхности усеченного конуса.
Ответ: 45
Скрыть
Sверхнего=$$\frac{S}{4}=\frac{60}{4}=15$$ (т.к. $$k=\frac{1}{2}$$; $$\frac{S_{1}}{S_{2}}=k^{2}$$)
$$60-15=45$$