ЕГЭ Профиль
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3371
Радиус основания конуса равен 3, а высота 4. Центр шара совпадает с центром основания конуса и касается боковой поверхности конуса. Найдите отношение объемов шара и конуса.
$$OB-R$$ конуса
$$OH-R$$ шара
из $$\bigtriangleup AOB$$: $$AB=\sqrt{OA^{2}+OB^{2}}=\sqrt{4^{2}+3^{2}}=5$$
$$OH=\frac{OA\cdot OB}{AB}=\frac{4\cdot3}{5}=2,4$$
Vконуса$$=\frac{1}{3}\cdot S_{osn}\cdot h=\frac{1}{3}\cdot\pi\cdot3^{2}\cdot4=12\pi$$
Vшара$$=\frac{4}{3}\cdot\pi\cdot R^{3}=18,432\pi$$
Vшара/Vконуса$$=\frac{18,432\pi}{12\pi}=1,536$$
Задание 4908
Во сколько раз уменьшится объем октаэдра, если все его ребра уменьшить в два раза?
Для решения данных заданий надо помнить, что периметры подобных фигур относятся как коэффициент подобия, площади - как квадрат коэффициента подобия, а объемы - как куб коэффициента подобия. То есть, если уменьшить ребро в два раза, объем изменится в 8 раз
Задание 5098
Для каждой грани куба с ребром 6 проделали сквозное квадратное отверстие со стороной квадрата 2. Найдите объем оставшейся части.
Внутри будет пространственный крест , состоящий из 7 кубов со стороной 2. Тогда его объем : $$V_{1}=2^{3}*7=56$$ Объем изначального куба: $$V=6^{3}=216$$ Объем оставшейся части: 216-56=160
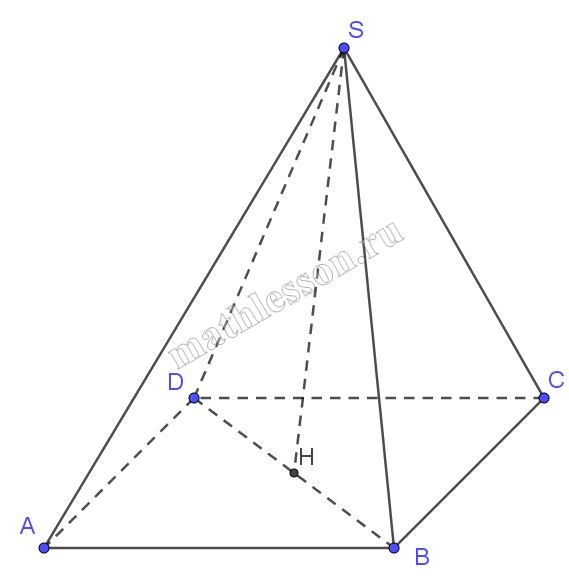
Задание 6563
Найдите объем октаэдра, ребро которого равно $$3\sqrt{2}$$ .
Рассмотрим четырехугольную пирамиду ABCDS с ребром $$3\sqrt{2}$$:
1)$$S_{ABCD}=(3\sqrt{2})^{2}=18$$
2) $$BD=\sqrt{(3\sqrt{2})^{2}+(3\sqrt{2})^{2}}=6\Rightarrow BH=3$$
3) $$\Delta BHS$$: $$SH=\sqrt{(3\sqrt{2})^{2}-3^{2}}=3$$
4) $$V_{ABCDS}=\frac{1}{3}*18*3=18$$
5) Тогда объем октаэдра : $$V=2*V_{ABCDS}=2*18=36$$
Задание 6966
В конус вписан цилиндр так, что плоскость его верхнего основания делит высоту конуса пополам. Найдите объем цилиндра, если объем конуса равен 12.
Пусть R-радиус основания большого конуса, h-его высота, тогда $$V=\frac{1}{3}\pi R^{2} h=12$$ – его объем . Пусть r-радиус основания цилиндра ,тогда: $$r=\frac{R}{2}$$ и m-его высота, тогда $$m=\frac{h}{2}$$ Объем цилиндра: $$V_{1}= \pi r^{2}m=\pi *\frac{R^{2}}{4}*\frac{h}{2}=$$$$\frac{\pi R^{2}h}{8}=\frac{36}{8}=4,5$$
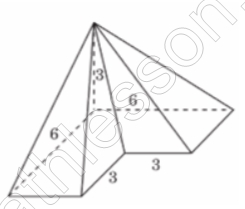
Задание 7033
Найдите объём пирамиды, изображённой на рисунке. Её основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых рёбер перпендикулярно плоскости основания и равно 3.
Найдем объем пирамиды без учета выреза: $$V_{1}=\frac{1}{3}*6*6*3=36$$
Найдем объем вырезанной: $$V_{2}=\frac{1}{3}*3*3*3=9$$
Найдем объем оставшейся: $$V=V_{1}-V_{2}=27$$