ЕГЭ Профиль
Задание 14432
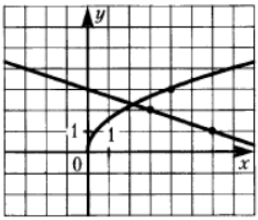
На рисунке изображён график функции $$f(x)=\frac{k}{x+a}$$.Найдите $$f(-7)$$.

Точка $$A(-4;1)$$ и $$B(-1;2)$$ принадлежат графику функции. Тогда:
$$\left\{\begin{matrix} -1=\frac{k}{-4a}\\ 2=\frac{k}{-1+a} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4-a=k\\ 2a-2=k \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4-a=2a-2\\ k=4-a \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=2\\ k=2 \end{matrix}\right.$$
Получим: $$f(-7)=\frac{2}{-7+2}=\frac{2}{-5}=-0,4$$
Задание 15261
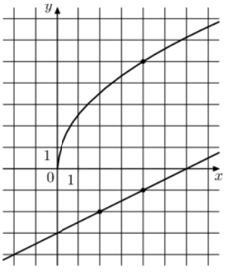
$$f(x)$$ проходит через $$(4;3).$$ Тогда:
$$3=a\cdot\sqrt{4}\Rightarrow a=\frac{3}{2}$$
Получим: $$f(x)=\frac{3}{2}\sqrt{x}.$$
$$g(x)$$ проходит через $$(0;3),$$ тогда $$b=3.$$ И через $$(3;2),$$ тогда: $$2=3k+3\Rightarrow k=-\frac{1}{3}$$
Получим: $$g(x)=-\frac{1}{3}x+3$$
$$-\frac{1}{3}x+3=\frac{3}{2}\sqrt{x}\Leftrightarrow -2x+18=9\sqrt{x}\Leftrightarrow\left\{\begin{matrix} 81x=324-72x+4x^2\\ -2x+18\geq0 \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} 4x^2-153x+324=0\\ x\leq9 \end{matrix}\right.\Leftrightarrow x=2,25$$
$$f(2,25)=\frac{3}{2}\cdot\sqrt{2,25}=1,5\cdot1,5=2,25$$
Задание 15400
Задание 15550
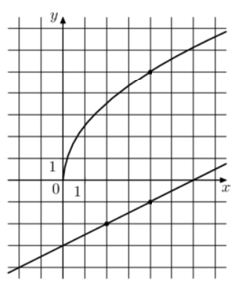
Угловой коэффициент прямой легко найти через тангенс $$\tg\alpha=k=0,5$$
$$b=−3$$
$$5\cdot a\cdot\sqrt{4},$$ откуда $$a=2,5$$
Теперь найдем точки пересечения:
$$2,5\sqrt{x}=0,5x-3$$ – решаем уравнение
$$x=36$$
$$f(36)=15$$
Задание 15828
График проходит через (4;7):
$$7=k\cdot\sqrt{4}\Rightarrow k=3,5$$
$$f(7,84)=3,5\sqrt{7,84}=3,5\cdot2,8=9,8$$