ЕГЭ Профиль
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1096
В трапеции АВСD (АВ||СD) угол АBС равен 130°. Окружность с центром в точке В проходит через точки А, D и С. Найдите величину угла ADC. Ответ дайте в градусах.
∠ ABC - центральный, а значит дуга AC, на которую он опирается, равна его величине, то есть 130°. Значит дуга CA (противоположная) равна: 360° - 130° = 230°. ∠ ADC опирается на эту дугу и он вписанный, значит равен половине величины дуги на которую он опирается, то есть 230°/2 = 115°
Задание 1925
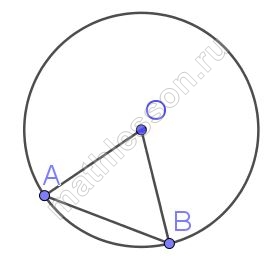
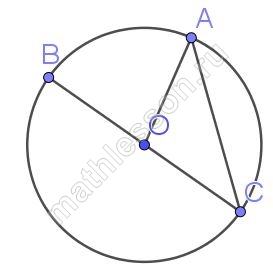
Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.
1) Треугольник AOB - равнобедренный (AO=OB - радиусы), тогда $$\angle OAB=\angle OBA=\frac{180-60}{2}=60^{\circ}$$, следовательно, OAB - равносторонний
2) Из п.1 получаем ,что AO=OB=AB=6
Задание 1926
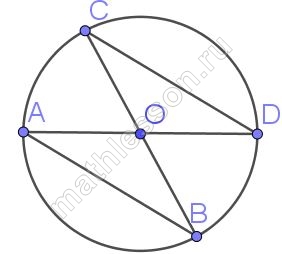
В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.
1) Треугольники COD и AOD равны, так как CO=OD=OA=OB (радиусы) и $$\angle COD=\angle AOD$$ (вертикальные углы)
2) Тогда $$\angle OAB=\angle CDO=\angle OCD=30^{\circ}$$
Задание 1927
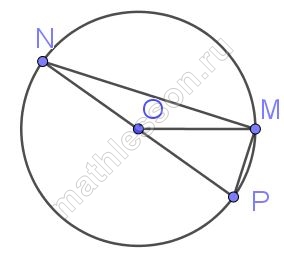
Найдите градусную меру ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.
1) Треугольник MON - равнобедренный (MO=ON - радиусы), тогда $$\angle ONM=\angle OMN$$
2) $$\angle MON=180-2*18=144^{\circ}$$
Задание 1928
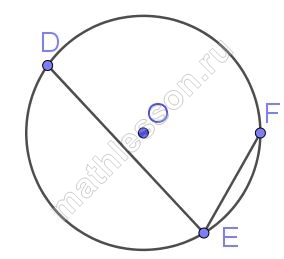
Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
1) $$\smile DF=360-150-68=142^{\circ}$$
2) $$\angle DEF=\frac{142}{2}=71^{\circ}$$ (по свойству вписанного угла)
Задание 1929
Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера ∠AOC равна 96°.
1) Треугольник OAC - ранвобедренный (OA=AC - радиусы), тогда $$\angle OAC=\angle OCA$$
2) $$\angle ACB=\angle ACO=\frac{180-96}{2}=42^{\circ}$$
Задание 1930
Найдите ∠KOM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°.
1) Меньшая дуга $$KM=KN-MN=180-124=56^{\circ}$$
2) $$\angle KOM=\smile MM-56^{\circ}$$ (по свойству центрального угла)
Задание 1931
В окружности с центром O AC и BD — диаметры. Угол ACB равен 26°. Найдите угол AOD. Ответ дайте в градусах.
1) $$\angle AOD=\angle COB$$ (по свойству вертикальных углов)
2) $$\angle COB=\angle OBC$$ (треугольник COB - равнобедренный, так как CO и OB - радиусы)
3) Из треугольника COB: $$\angle COB=180-2*26=128^{\circ}$$, тогда и $$\angle AOD=128^{\circ}$$
Задание 1932
Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?

1) Радиус описанной окружности около прямоугольного треугольника равен половине его гипотенузы. Пусть R - радиус описанной окружности
2) По теореме Пифагора из треугольника ABC: $$AC=\sqrt{12^{2}+5^{2}}=13$$, тогда $$R=\frac{1}{2}AC=6,5$$
Задание 1933
Точки A и B делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
1) Пусть меньшая дуга 9х, тогда большая дуга 11х
2) $$9x+11x=360\Leftrightarrow$$$$x=18$$ (по свойству градусной меры окружности), тогда меньшая дуга составляет $$9x=9*18=162$$
3) $$\angle AOB=\smile AOB=162^{\circ}$$ (по свойству центрального угла)
Задание 1934
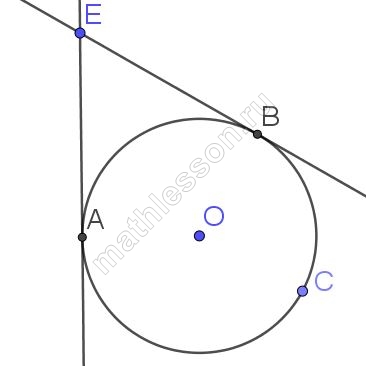
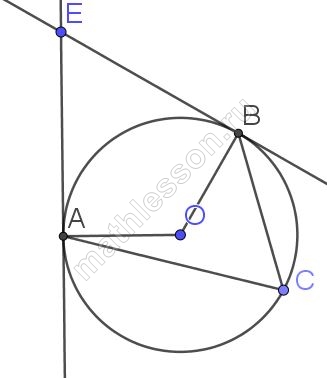
В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B. На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB.
1) OA и OB перпенидулярны сторонам угла (по свойству касательной и радиуса в точку касания)
2) Из четырехугольника AEOB: $$\angle AOB=360-2*90-70=110^{\circ}$$ (по свойству суммы углов выпуклого четырехугольника)
3) $$\angle ACB=\frac{1}{2}\angle AOB=55^{\circ}$$ (по свойству вписанного и центрального угла)