ЕГЭ Профиль
Задание 14396


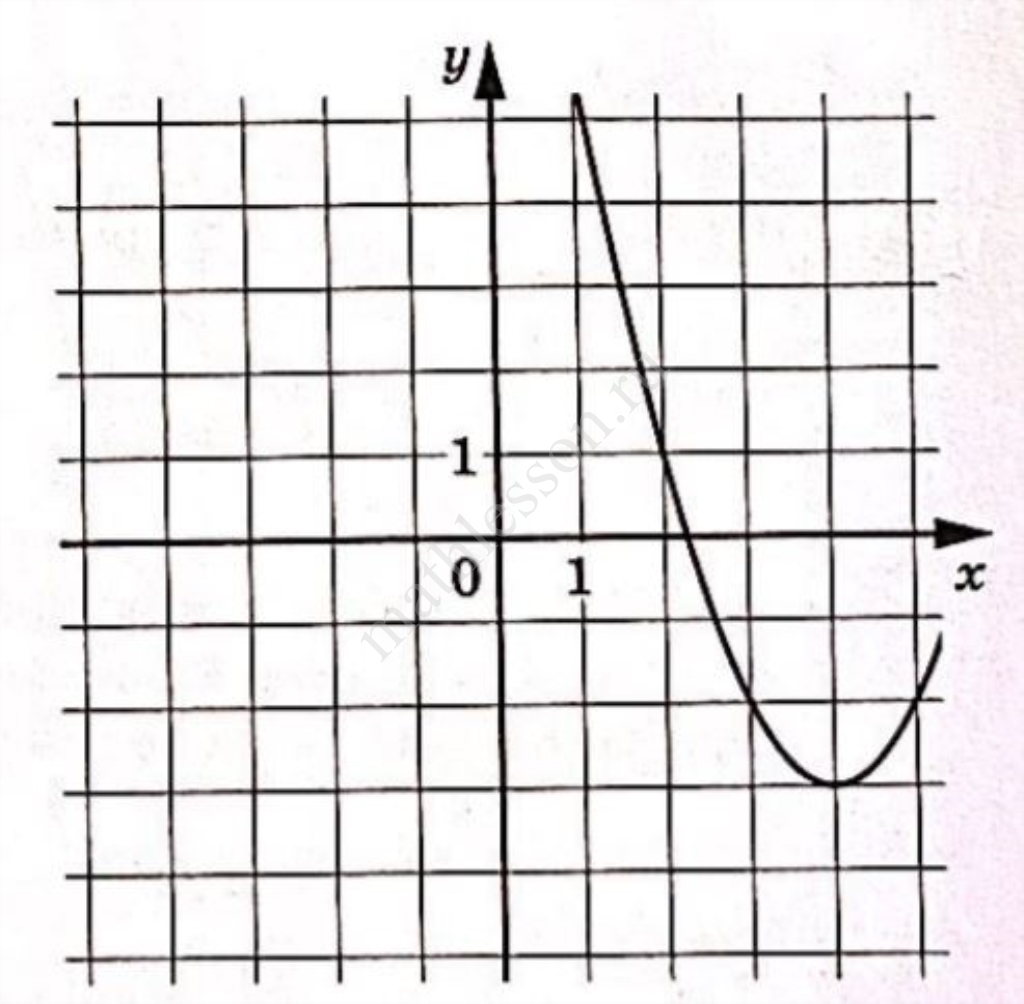
Коэффициент c всегда равен координате пересечения параболы оси $$Oy$$: $$c=-4$$Возьмём точку принадлежащую параболе $$(1:1)$$ подставим её координаты и значение $$c$$ в функцию, найдём $$b$$:
$$1=2\cdot1^2+b\cdot1-(-4)$$
$$b=3$$
Функция имеет вид:
$$f(x)=2x^2+3x-4$$
Найдём $$f(-5)$$:
$$f(-5)=2\cdot(-5)^2+3\cdot(-5)-4=50-15-4=31$$
Задание 14414
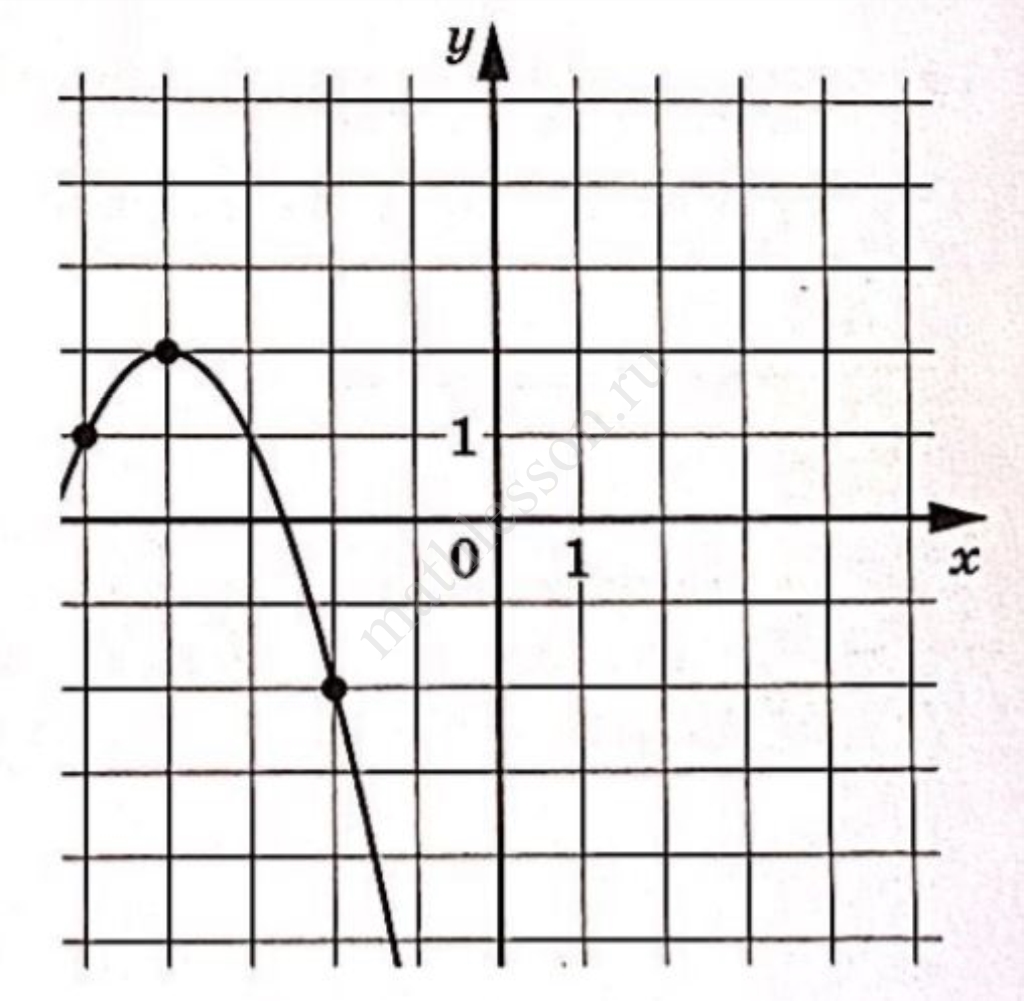
На рисунке изображён график функции $$f(х)=ах^2+8х+с$$. Найдите $$f(6)$$.

Точки $$A(1;2)$$ и $$B(4;-4)$$ принадлежат графику функции. Тогда:
$$\left\{\begin{matrix} 2=a+8+c\\ -4=16a+32+c \end{matrix}\right. \left\{\begin{matrix} a+c=-6\\ -6=15a+24 \end{matrix}\right. \left\{\begin{matrix} a=-2\\ c=-4 \end{matrix}\right.$$
$$f(x)=-2x^2+8x-4$$
$$f(6)=-72+48-4=-28$$
Задание 14492

Учтём, что абсцисса вершины параболы для $$f(x): x_0=-\frac{-5}{2\cdot2}=1,25$$ - правая парабола.
Левая парабола пересекает $$Oy$$ в $$(0;-3),$$ значит, $$c=-3.$$
Точки $$A(1;1)$$ и $$B(-2;-5)$$ принадлежат $$g(x)=ax^2+bx+c.$$ Тогда:
$$\left\{\begin{matrix} 1=a\cdot1^2+b\cdot1-3\\ -5=a\cdot(-2)^2+b\cdot(-2)-3 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 4=a+b\\ -2=4a-2b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 4=a+b\\ -1=2a-b \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} a=4-b\\ -1=8-2b-b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=1\\ b=3 \end{matrix}\right.$$
Получили:
$$g(x)=x^2+3x-3$$
Тогда:
$$x^2+3x-3=2x^2-5x+4$$
$$x^2-8x+7=0$$
$$\left[\begin{matrix} x_1=1\Rightarrow y_1=1+3-3=1\\ x_2=7\Rightarrow y_2=49+21-3=67 \end{matrix}\right.$$
Задание 14509

Абсцисса вершины для $$f(x): x_0=-\frac{(-2)}{(-2)\cdot2}=-\frac{1}{2}$$
Это правая парабола.
$$g(x)\cap Oy$$ в точке $$(0;1),$$ значит $$c=1.$$
Точки $$A(-2;5)$$ и $$C(-4;1)$$ принадлежат $$g(x).$$ Тогда:
$$\left\{\begin{matrix} 5=a\cdot(-2)^2+b\cdot(-2)+1\\ 1=a\cdot(-4)^2+b\cdot(-4)+1 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 4=4a-2b\\ 0=16a-4b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 2=2a-b\\ 4a=b \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} 2=2a-4a\\ b=4a \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=-1\\ b=-4 \end{matrix}\right.$$
Получили $$g(x)=-x^2-4x+1$$
Тогда:
$$-2x^2-2x+4=-x^2-4x+1$$
$$x^2-2x-3=0$$
$$\left[\begin{matrix} x_1=3\\ x_2=-1 \end{matrix}\right.$$
Задание 14524

Для того чтобы найти $$f(-18)$$ нам необходимо знать уравнение прямой, то есть значение коэффициентов k и b.
Прямая проходит через точки $$(3;-1)$$ и $$(-4;-3).$$ Подставим их координаты в уравнение прямой:
$$-1=3k+b$$ (1)
$$-3=-4k+b$$ (2)
Вычтем из (1) уравнения (2):
$$-1-(-3)=3k+b-(-4k+b)$$
Раскроем скобки:
$$-1+3=3k+b+4k- b$$
Приведем подобные слагаемые в обеих частях уравнения:
$$2=7k$$
Найдем k:
$$k=\frac{2}{7}$$
Найдем b из (1), подставив в него значение коэффициента $$k = \frac{2}{7}:$$
$$-1=3\cdot\frac{2}{7}+b$$
$$-1=\frac{6}{7}+b$$
$$b=-1-\frac{6}{7}$$
$$b=-\frac{13}{7}$$
Получим следующее уравнение прямой:
$$f(x)=\frac{2}{7}\cdot x-\frac{13}{7}$$
Найдем $$f(-18):$$
$$f(-18)=\frac{2}{7}\cdot(-18)-\frac{13}{7}$$
$$f(-18)=-\frac{36}{7}-\frac{13}{7}$$
$$f(-18)=-\frac{49}{7}$$
$$f(-18)=-7$$
Задание 14540

Точки $$(3;-3)$$ и $$(-1;4)$$ принадлежат графику функции. Тогда:
$$\left\{\begin{matrix} -3=k\cdot3+b\\ 4=k\cdot(-1)+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -7=4k\\ b=4+k \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} k=-\frac{7}{4}\\ b=\frac{9}{4} \end{matrix}\right.$$
Получили:
$$f(x)=-\frac{7}{4}x+\frac{9}{4}$$
Тогда:
$$-\frac{7}{4}x+\frac{9}{4}=-20,5$$
$$-7x+9=-82$$
$$-7x=-91$$
$$x=13$$
Задание 14555

Точки $$(0;5)$$ и $$(-2;-3)$$ принадлежат графику $$g(x).$$ Тогда:
$$\left\{\begin{matrix} 5=\alpha\cdot0+b\\ -3=\alpha\cdot(-2)+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=5\\ -3=-2\alpha+5 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=5\\ \alpha=4 \end{matrix}\right.$$
Получили:
$$g(x)=4x+5$$
Точки $$(0;5)$$ и $$(-2;-3)$$ принадлежат графику $$f(x).$$ Тогда:
$$-2=\frac{k}{-3}$$
$$k=6$$
Получили:
$$f(x)=\frac{6}{x}$$
Тогда:
$$4x+5=\frac{6}{x}\Rightarrow\left\{\begin{matrix} 4x^2+5x-6=0\\ x\neq0 \end{matrix}\right.$$
$$D=25+96=121$$
$$x_1=\frac{-5+11}{8}=0,75$$
$$x_2=\frac{-5-11}{8}=-2$$
Задание 14560

Точки $$(4;-2)$$ и $$(-4;-5)$$ принадлежат графику $$g(x).$$ Тогда:
$$\left\{\begin{matrix} -2=\alpha\cdot4+b\\ -5=\alpha\cdot(-4)+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -7=2b\\ a=\frac{-2-b}{4} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=-3,5\\ a=\frac{-2+3,5}{4}=\frac{3}{8} \end{matrix}\right.$$
Точка $$(4;-1)$$ принадлежит графику функции $$f(x).$$ Тогда:
$$-1=\frac{k}{4}\Leftrightarrow k=-4$$
Получили:
$$f(x)=-\frac{4}{x}$$
$$g(x)=\frac{3}{8}x-\frac{7}{2}$$
Тогда:
$$\frac{3}{8}x-\frac{7}{2}=-\frac{4}{x}\Leftrightarrow\left\{\begin{matrix} 3x^2-28x+32=0\\ x\neq0 \end{matrix}\right.$$
$$\frac{D}{4}=(14)^2-3\cdot32=100$$
$$x_1=\frac{14+10}{3}=8$$
$$x_2=\frac{14-10}{3}=\frac{4}{3}$$
Ордината $$B:$$
$$f(8)=-\frac{4}{8}=-0,5$$
Задание 14601

$$f(x)$$ проходит через $$(-7;2)$$ и $$(-2;4).$$ Тогда:
$$\left\{\begin{matrix} 2=-7k+b\\ 4=-k+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 2=-2,8+b\\ 2=5k \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=4,8\\ k=0,4 \end{matrix}\right.$$
Получили: $$f(x)=0,4x+4,8$$
Тогда: $$f(-10)=0,4\cdot(-10)+4,8=0,8$$
Задание 14607
На рисунке изображена часть графика функции $$f(x)=|kx+b|.$$ Найдите $$f(-15).$$

$$f(x)$$ проходит через $$(-2;4)$$ и $$(-7;2).$$
При этом изображено "положительное" раскрытие модуля, т. е. $$f(x)=kx+b,k\geq0.$$
Получим:
$$\left\{\begin{matrix} 4=-2k+b\\ 2=-7k+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} k=0,4\\ b=4,8 \end{matrix}\right.$$
Получим:
$$f(x)=|0,4x+4,8|, тогда: f(-15)=|0,4\cdot(-15)+4,8|=|-1,2|=1,2.$$
Задание 14659

Пусть $$f(x)=a(x-m)^2+n.$$ Вершина смещена относительно $$(0;0)$$ на 5 вправо $$\Rightarrow m=5$$ и на 2 вниз $$\Rightarrow n=-2.$$ Наклон параболы стандартный (соответствует $$y=x^2$$), значит $$a=1.$$ Получим $$f(x)=(x-5)^2-2.$$
Тогда $$f(-1)=(-1-5)^2-2=36-2=34$$
Задание 14796

Правый график уже, значит модуль коэффициента при $$x^2$$ у него больше, т.е. это $$f(x).$$
$$g(x)$$ проходит через $$(0;3),$$ значит $$c=3$$ и через $$(-1;1)$$ и $$(1;3).$$ Тогда:
$$\left\{\begin{matrix} 1=a\cdot(-1)^2+b\cdot(-1)+3\\ 3=a\cdot1^2+b\cdot1+3 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -2=a-b\\ 0=a+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 2a=-2\\ 2b=2 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=-1\\ b=1 \end{matrix}\right.$$
Получили $$g(x)=-x^2+x+3.$$ Тогда:
$$-2x^2+7x-2=-x^2+x+3\Rightarrow x^2-6x+5=0\Rightarrow\left[\begin{matrix} x=1\\ x=5 \end{matrix}\right.$$
Тогда $$B_x=5$$