ЕГЭ Профиль
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 900
Найдите радиус окружности, описанной около треугольника АВС, если известно, что ∠С = 90°, ВС=6, cos B = 2/3.
AB = BC / cos B = 6 * 3 / 2 = 9 Радиус описанной окружности вокруг прямоугольного треугольника равен половине гипотенузы. Получаем 9 / 2 = 4,5
Задание 1174
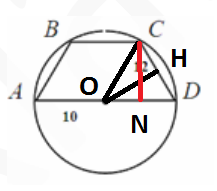
Трапеция АВСD вписана в окружность с диаметром АD. Найдите высоту трапеции, если радиус окружности равен 10, а боковая сторона трапеции равна 12.
Достроим треугольник OCD: OC = OD = 10 - радиусы, OH, CN - высоты. HD = 6 (OH - высота, биссектриса и медиана), отсюда по теореме Пифагора OH = $$\sqrt{OD^{2}-HD^{2}}=8$$.Тогда, используя формулу площади треугольника, получаем:
$$\frac{1}{2} OH*CD = \frac{1}{2} CN*OD$$
$$CN=\frac{OH*CD}{OD}=\frac{8*12}{10}=9.6$$
Задание 1919
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABH.
1) Для нахождения угла правильного n-угольника, можно воспользоваться формулой: $$\alpha=\frac{n-2}{n}*180$$
2) $$\angle ABC = \frac{8-2}{8}*180=135^{\circ}$$
3) Из треугольника HOA: $$\angle HOA=180-2\angle OHA=180-\angle H=45^{\circ}$$ (треугольник равнобедренный, OH - биссектрисса угла H)
4) Меньшая дуга $$HA=\angle HOA=45^{\circ}$$ (по свойству центрального угла)
5) $$\angle ABH=\frac{1}{2}\smile HA=22,5^{\circ}$$ (по свойству вписанного угла)
Задание 1921
Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
1) $$\angle ABC=\frac{1}{2}\smile AC$$ (по свойству вписанного угла), тогда $$\smile AC=2*120=240^{\circ}$$ (большая дуга)
2) Вся окружность равна $$360^{\circ}$$, тогда меньшая дуга AC составляет $$120^{\circ}$$
3) $$\angle AOC=\smile AC=120^{\circ}$$ (меньшей дуге, по свойству центрального угла), тогда треугольники ABC и AOC равны (оба равнобедренных, общая сторона), следовательно OC=4, и диаметр составляет 4*2=8
Задание 1922
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.
1) Треугольник ABC - равнобедренный, $$\angle BAC=\angle BCA=\frac{180-177}{2}=1,5$$.
2) $$\angle BAC=\frac{1}{2}BC$$ (по свойству вписанного угла), тогда $$\smile BC=2*1,5=3^{\circ}$$
3) $$\angle BOC=\smile BC=3^{\circ}$$ (по свойству центрального угла)
Задание 1923
Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
1) $$\angle ABC=\frac{1}{2}\smile AC$$ (по свойству вписанного угла), тогда $$\smile AC=140^{\circ}$$
2) $$\angle CAD=\frac{1}{2}\smile DC$$ (по свойству вписанного угла), тогда $$\smile DC=98^{\circ}$$
3) $$\smile AD=140-98=42^{\circ}$$, тогда $$\angle ABD=\frac{1}{2}\smile AD=21^{\circ}$$ (по свойству вписанного угла)
Задание 3572
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно $$95^{\circ}$$, $$49^{\circ}$$, $$71^{\circ}$$, $$145^{\circ}$$
. Найдите угол B этого четырехугольника. Ответ дайте в градусах.
-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 54°. Найдите n.
Задание 3853
Четырёхугольник ABCD вписан в окружность, причём BC =CD. Известно, что угол ADC равен 93°. Найдите, под каким острым углом пересекаются диагонали этого четырёхугольника. Ответ дайте в градусах.
1) $$\bigtriangleup AOD\sim \bigtriangleup COB$$ $$\Rightarrow$$
$$\angle ADO=\angle OCB=\alpha$$
$$\angle DAO=\angle OBC=\beta$$
2) $$\bigtriangleup DOC\sim \bigtriangleup AOB$$ $$\Rightarrow$$
$$\bigtriangleup DCB$$ - равнобедренный
$$\angle COB=\angle DCB=\beta$$ $$\Rightarrow$$ $$\alpha+\beta=93^{\circ}$$
$$\angle AOD=180^{\circ}-\alpha-\beta=87^{\circ}$$
Задание 4811
Точка O—центр описанной окружности остроугольного треугольника ABC. Найдите ∠ABC, если $$\angle OCA=37^{\circ}$$. Ответ дайте в градусах.
Если рассмотреть треугольник AOC, то он окажется равнобедренным, так как OA = OC - радиусы. В таком случае: $$\angle AOC = 180 -2*37=106^{\circ}$$. Но данный угол центральный, в то время как ∠ABC - вписанный, и тогда его градусная мера равна половине градусной меры ∠AOC, то есть 53
Задание 6797
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Центр лежит на пересечении серединных перпендикуляров $$\angle A=60\Rightarrow$$ $$\angle B=120$$
Пусть BM – биссектриса $$\Rightarrow$$ $$\angle ABM =60\Rightarrow$$ $$\Delta ABM$$ - равносторонний . Пусть CH- биссектриса $$\Rightarrow$$ $$\angle CMD=60\Rightarrow$$ $$\Delta CMD$$ - равносторонний и $$\Delta ABM=\Delta BMC=\Delta CMD$$(M и H совпадают )$$\Rightarrow$$ $$AB=BM=MC=MD$$ - радиусы $$\Rightarrow$$ $$R=6$$
Задание 7011
Четырёхугольник ABCD вписан в окружность, причём BC =CD. Известно, что угол ADC равен 930 . Найдите, под каким острым углом пересекаются диагонали этого четырёхугольника. Ответ дайте в градусах.
1) $$\angle ADC=93$$, пусть $$\angle CDB=\alpha$$$$\Rightarrow$$ $$\angle CBD =\alpha$$ 2) $$\angle ADB=\angle ADC-\angle CDB=93-\alpha$$ . Но $$\angle ACB=\angle ADB$$(опирают на одну дугу )$$\Rightarrow$$ из $$\Delta CHB$$ ($$AC \cap DB=H$$): $$\angle CHB=180-(93-\alpha +\alpha )=87$$
Задание 10548
Найдите площадь треугольника АВС, изображенного на рисунке.
Задание 10648
В треугольнике MNP известно, что $$MM_1$$ и $$PP_1$$ - медианы, $$MM_1=9\sqrt{3},PP_1=6,\angle MOP=150{}^\circ .$$ Найдите радиус окружности, описанной около треугольника $$MOP$$.
Задание 10871
Задание 12845
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 72$${}^\circ$$, угол CAD равен 58$${}^\circ$$. Найдите угол АВС. Ответ дайте в градусах.
Угол ∠АВD = 72° – вписанный в окружность угол. Вписанный в окружность угол измеряется половиной дуги, на которую он опирается, следовательно, дуга АD = 144°.
Угол ∠CAD = 58° – вписанный в окружность угол, следовательно, дуга CD = 116°.
Дуга AC = AD + DC AC = AD + DC = 144° + 116° = 260°
Угол ∠ABC – вписанный в окружность угол, который опирается на дугу АС, следовательно, ∠AВС = 130°.
