ЕГЭ Профиль
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 973
Прямая y=3х+4 является касательной к графику функции у=х2‐3x‐c. Найдите c.
Так как прямая является касательной, то мы можем приравнять производные данных функций, чтобы найти абсциссу точки касания: 3 = 2x - 3. Отсюда x = 3. Так же мы можем приравнять сами функции и подставить найденную абсциссу:
3x+4=х2‐3x‐c
3*3+4=32-3*3-с
13=-c, отсюда с = -13
Задание 1097
К графику функции у = f (x) в точке с абсциссой х0 проведена касательная, которая перпендикулярна прямой, проходящей через точки (4; 3) и (3; ‐1) этого графика. Найдите f / (x0).
Пусть прямая, проходящая через точки (4; 3) и (3; ‐1) задается формулой y = k1x+b. Найдем k1, подставив имеющиеся координаты в уравнение прямой:
$$\left\{\begin{matrix}3=4*k_{1}+b\\ -1=3*k_{1}+b\end{matrix}\right.$$ Найдем $$k_{1}$$. Решив систему получим, что $$k_{1}=4$$ Далее воспользуемся свойством: если k1 и k2 угловые коэффициенты двух линейных функций, то их графики буду перпендикулярны в том случае, когда k1k2=-1. Получаем, что k2=-1/k1=-1/4=-0.25. А значение производной в точке и есть величина углового коэффициента.
Задание 1236
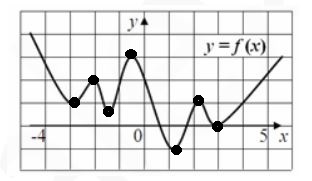
По графику функции у = f (x) определите количество точек на интервале (4;5), в которых касательная к графику параллельна оси абсцисс или совпадает с ней.
Если касательная параллельна оси ОХ, то производная равна 0. Производная равна нулю на данном графике функции в точках максимума и минимума ( они отмечены жирной точкой ). Их всего 7
Задание 1277
На рисунке приведен график f ' (x) – производной функции у = f (x). Определите абсциссу точки графика функции у = f (x), в которой касательная параллельна прямой у = 2х – 1 или совпадает с ней.
Так как касательная к графику параллельна или совпадает с прямой y = 2x - 1, и при этом значение производной равно коэффициенту k линейной функции ( в нашем случае этот коэффициент равен 2 ), то и значение производной, которое мы ищем, равно 2. А так как нам дан график производной, то мы смело находим точку с ординатой (ось Оу) равную 2 и ищем абсциссу этой точки. Она равна -3
Задание 2823
На рисунке изображён график функции $$y=f(x)$$. На оси абсцисс отмечены точки -2, -1, 2, 3. В какой из этих точек значение производной наибольшее? В ответе укажите
эту точку.
2 - т.к. там функция возрастает $$\Rightarrow$$ производная положительная; в -1 тоже возрастает, но если провести касательную, то угол будет меньше, чем в $$x=2$$.
Задание 2899
Прямая $$y=-4x-11$$ является касательной к графику функции $$y=x^{3}+7x^{2}+7x-6$$. Найдите абсциссу точки касания.
$$f'=-4x-11x^{3}+7x^{2}+7x-6=g$$ $$f'=-4$$ $$g'=3x^{2}+14x+7$$ $$f'=g'$$ $$\Rightarrow$$ $$3x^{2}+14x+7=-4$$ $$3x^{2}+14x+11=0$$ $$D=196-132=64$$ $$x_{1}=\frac{-14+8}{6}=-1$$ $$x_{1}=\frac{-14-8}{6}=-\frac{11}{3}$$ $$f(-1)=-4(-1)-11=-7$$ $$g(-1)=(-1)^{3}+7\cdot (-1)^{2}+7\cdot (-1)-6=-7$$ $$f(-1)=g(-1)$$ $$\Rightarrow$$ абсцисса -1
Задание 3028
Прямая $$y=7x-5$$ параллельна касательной к графику функции $$y=x^{2}+6x-8$$. Найдите абсциссу точки касания.
$$\left\{\begin{matrix}7x-5=x^{2}+6x-8\\7=2x+6\end{matrix}\right.$$ $$2x=1$$ $$x=0,5$$
Задание 3070
На рисунке приведен график производной $${g}'(x)$$, на графике отмечены шесть точек: х1, х2, …, х6. Сколько из этих точек принадлежит промежуткам возрастания функции g(x)?
Функция возрастает там, где $${g}'(x)>0$$ $$\Rightarrow$$ $$x_{1};x_{2};x_{3};x_{4};x_{6}$$
Задание 3152
На рисунке приведен график функции у=g(x). На графике отмечены шесть точек: х1, х2, …, х6. В скольких из этих точек производная g/(x) принимает положительные значения?
Производная принимает положительные значения там, где функция возрастает: на рисунке это точки х2,х5 и х6
Задание 3197
Прямая $$y=-9x+5$$ является касательной к графику функции $$f(x)=ax^{2}+15x+11$$. Найдите a.
$$\left\{\begin{matrix}-9=2ax+15\\-9x+5=ax^{2}+15x+11\end{matrix}\right.$$ $$\Leftrightarrow$$ $$x=-\frac{12}{a}$$ $$-9x+5-ax^{2}-15x-11=0$$ $$ax^{2}+24x+6=0$$ $$a\cdot\frac{144}{a^{2}}-\frac{288}{a}+6$$ $$-\frac{144}{a}=-6$$ $$a=\frac{144}{6}=24$$
Задание 3242
Функция у = f (x) определена на промежутке [‐4; 5]. На рисунке приведен график её производной. Найдите количество точек графика функции у = f (x), касательная в которых параллельна прямой 5х – 2у = 1 или совпадает с ней.
$$5x-2y=1$$ $$5x-1=2y$$ $$\Leftrightarrow$$ $$y=\frac{5x}{2}-\frac{1}{2}$$ $$y'=\frac{5}{2}$$ $$\Rightarrow$$ 4 точки
Задание 3323
На рисунке изображен график функции y=f(x), определенной на интервале (−5;8). Определите количество целых точек, в которых производная функции отрицательна.
Значение производной отрицательное в том случае, если функция убывает. Функция убывает на промежутке от -2 до 0, причем -2 и 0 это точки экстремума, и, следовательно, там производная равна 0, а значит отрицательна она только в -1 (если рассматривать только целые абсциссы), на промежутке от 2 до 5,5 (примерно), 2 так же точка экстремума, значит мы считаем только 3; 4; 5 и на промежутке от 7 до 8, где 7 и 8 точки экстремум, то есть нас устраивающих точек нет. В итоге всего 4 точки
Задание 3598
Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.
Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).