ЕГЭ Профиль
Задание 1289
В треугольнике АВС угол С равен 90º. Площади квадратов АВРК и АСЕМ равны 16 и 12 соответственно. Найдите площадь квадрата СВNT.
Задание 2984
Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Периметры подобных фигур относятся как коэффициент подобия. То есть в нашем случае k=3/5 Площади подобных фигур относятся как квадрат коэффициента подобия. Пусть х - площадь большей фигуры, тогда: $$\frac{18}{x}=\frac{9}{25}$$ $$x=\frac{25*18}{9}=50$$
Задание 4388
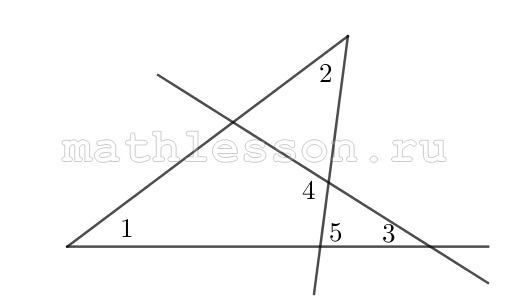
В треугольнике ABC известно, что $$\angle A=30^{\circ}$$ и $$\angle B=86^{\circ}$$. CD—биссектриса внешнего угла при вершине C, причём D лежит на прямой AB. На продолжении стороны AC за точку C выбрана точка E так, что CB = CE. Найдите $$\angle ADE$$. Ответ дайте в градусах.
из $$\bigtriangleup ABC$$: $$\angle C=180-\angle A-\angle B=180-30-86=64^{\circ}$$; $$\angle BCE=180-\angle C=180-64=116^{\circ}$$; $$\angle BCD=\frac{1}{2}\angle BCE=116\div2=58^{\circ}$$ (CD - биссектриса); $$\angle ADC=180-\angle A-\angle ADC=180-\angle A-\angle ACB-\angle BCD=180-30-64-58=28^{\circ}$$; $$BC=CE$$; $$\angle BCD=\angle ECD$$; CD - общая $$\Rightarrow$$ $$\bigtriangleup BCD=\bigtriangleup CED$$ $$\Rightarrow$$ $$\angle CDE=28^{\circ}$$ $$\Rightarrow$$ $$\angle ADE=2\cdot28=56^{\circ}$$
Задание 6318
На рисунке AB=4, BE=8, DE=5, прямая AB перпендикулярна прямой BD, CD перпендикулярна BD, EA перпендикулярна EC. Найдите CD.
Пусть $$\angle A=\alpha$$, тогда $$\angle AEB=90-\alpha$$. Но тогда $$\angle CED=\alpha$$, следовательно, треугольники ABE и CED подобны. Из подобия получаем отношение: $$\frac{AB}{BE}=\frac{ED}{CD}$$. Тогда $$CD=\frac{ED*BE}{AB}=\frac{5*8}{4}=10$$
Задание 7192
В правильном шестиугольнике АВСDEF $$AD=2\sqrt{3}$$ . Найдите АЕ.
По свойству правильного шестиугольника: $$\angle D=120$$ ; $$\angle CDA=\angle ADE=\frac{\angle D}{2}=60$$; $$AE\perp DE\Rightarrow$$ из $$\Delta ADE$$: $$AE=AD*\cos DAE=2\sqrt{3}\cos 30=$$$$2\sqrt{3}*\frac{\sqrt{3}}{2}=3$$
Задание 15920
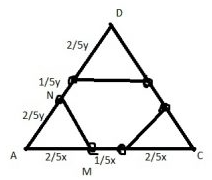
Треугольник AMN подобен ADC с коэффициентом подобия $$k=\frac{x}{\frac{2}{5}x}=2,5$$
$$S_{AMN}=\frac{100}{2,5^2}=16$$
Аналогично с остальными двумя (очевидно, что они будут равны)
В итоге $$S_{шест}=100−3\cdot16=52$$
Задание 16001
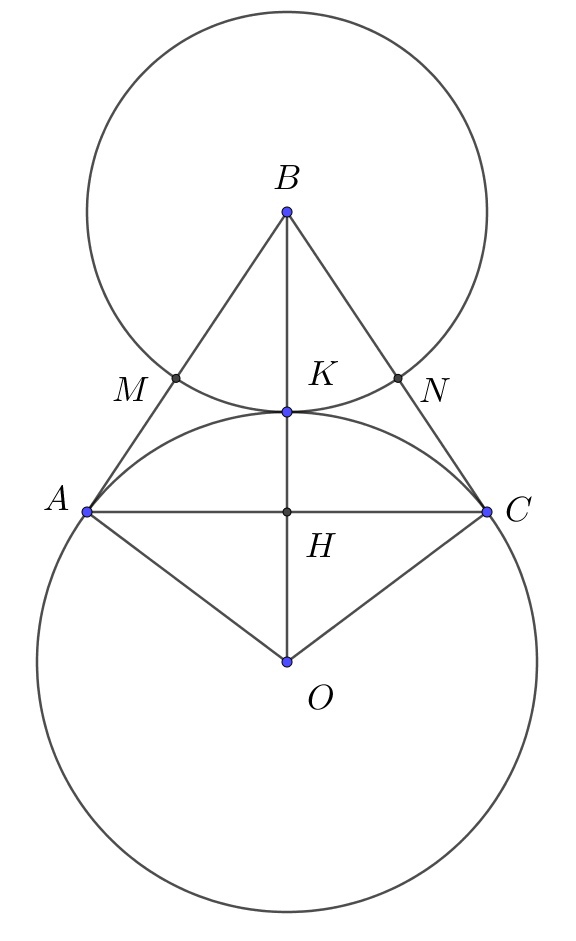
Пусть O - центр второй окружности. BH - высота $$\Delta ABC$$.
$$BH=\sqrt{25^2-15^2}=20$$. Тогда $$BK=15$$ и $$HK=20-15=5$$. При этом $$OK=OC=R$$ - радиусы второй окружности.
$$(R-5)^2+15^2=R^2\Leftrightarrow R^2-10R+25+225=R^2\Rightarrow R=25$$.
Задание 16021
Если четырехугольник можно вписать в окружность, то суммы противоположных сторон равны друг другу
$$3+x=10+8$$
$$x=15$$
Зная все стороны, мы знаем периметр и полупериметр.
Теперь вспоминаем формулу Герона
$$p=\frac{10+3+8+15}{2}=18$$
$$S=\sqrt{(p−10)(p−3)(p−8)(p−15)}=60$$
Задание 16162
Тут можно рассмотреть несколько случаев, когда высоты треугольников лежат по одну сторону от AC и нет. Но ответ конечно же не изменится.
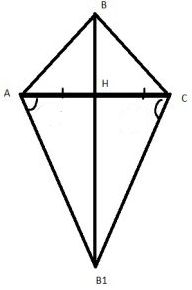
Рассмотрим такой рисунок, когда B и B1 находится на противоположных сторонах (остальные случаи рассматриваются аналогично)
$$\frac{S_{AB_1C}}{S_{ABC}}=\frac{0,5AC\cdot B_1H}{0,5AC\cdot BH}=\frac{B_1H}{BH}=3$$
Так как AB1C- равносторонний, то все его углы по 60, и высота – это и медиана и биссектриса
$$\tg60=\frac{B_1H}{AH}$$
$$B_1H=\tg60\cdot AH=\frac{\sqrt{3}}{2}AC$$ $$(AH=0,5AC)$$
Значит, $$BH=\frac{AC}{2\sqrt{3}}$$
$$tg\angle BAH=\frac{BH}{0,5AC}=\frac{1}{\sqrt{3}}$$
Значит, $$\angle BAH=30$$
и значит, наибольший угол будет $$\angle ABC=180-(30+30)=120$$
Задание 16259
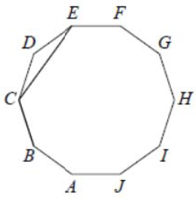
Вокруг любого правильного многоугольника можно описать окружность.
Центральный угол EOB равен $$\frac{360^{\circ}}{10}\cdot3=108^{\circ}$$.
Тогда большая дуга EB равна $$360^{\circ}-108^{\circ}=252^{\circ}$$.
Угол BCE опирается на ту же дугу EB, но является вписанным, поэтому равен половине дуги EB, т. е. $$126^{\circ}$$.