ЕГЭ Профиль
Задание 14432
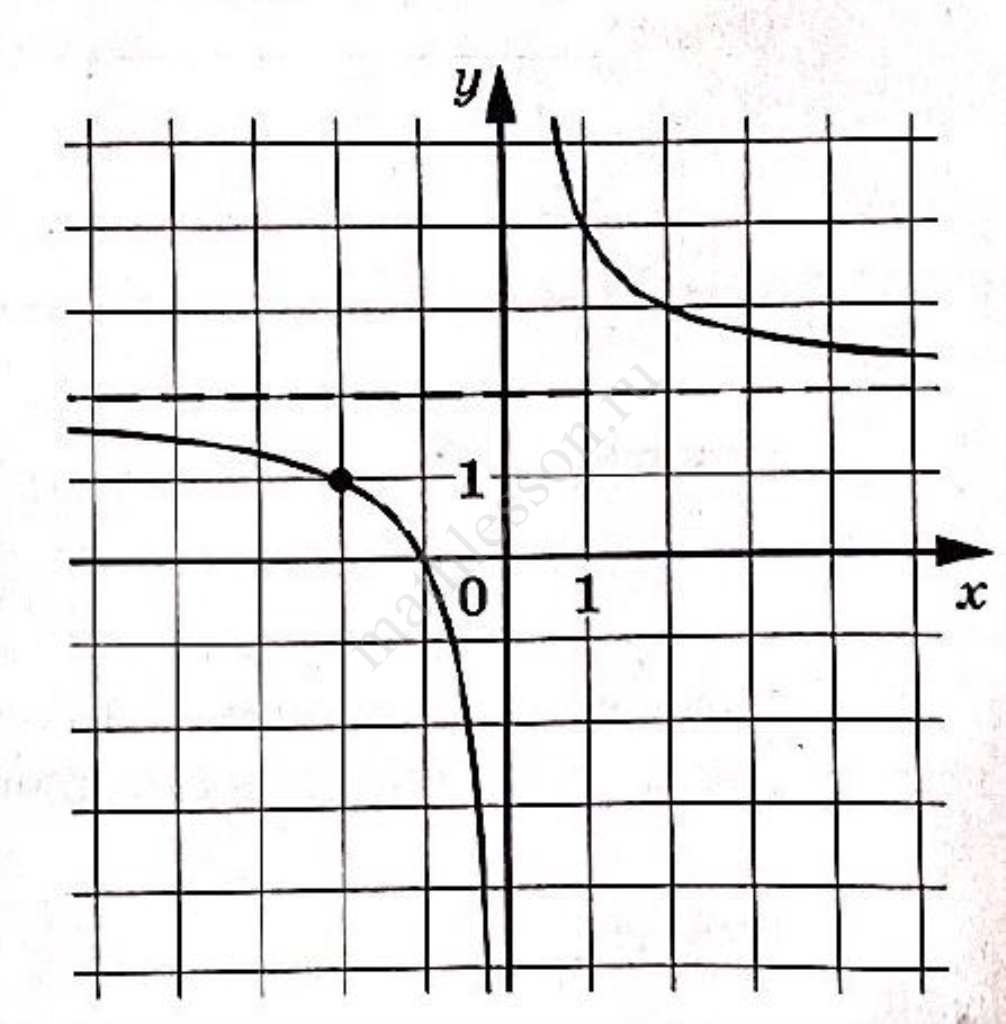
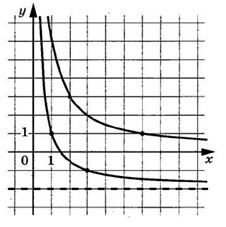
На рисунке изображён график функции $$f(x)=\frac{k}{x+a}$$.Найдите $$f(-7)$$.

Точка $$A(-4;1)$$ и $$B(-1;2)$$ принадлежат графику функции. Тогда:
$$\left\{\begin{matrix} -1=\frac{k}{-4a}\\ 2=\frac{k}{-1+a} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4-a=k\\ 2a-2=k \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4-a=2a-2\\ k=4-a \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=2\\ k=2 \end{matrix}\right.$$
Получим: $$f(-7)=\frac{2}{-7+2}=\frac{2}{-5}=-0,4$$
Задание 14449

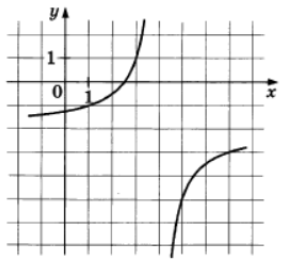
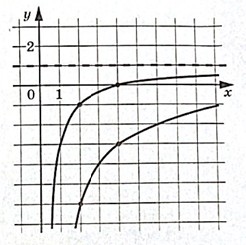
Вертикальная асимптота графика гиперболы проходит через точку $$x=2,$$ следовательно, параметр $$a=-2.$$
Второй параметр k вычислим из координаты точки $$(-1; -1)$$ на графике:
$$-1=\frac{k}{-1-2}\Rightarrow k=3$$
Получаем график гиперболы:
$$f(x)=\frac{3}{x-2}$$
Найдем точку x, при которой $$f(x)=-0,2:$$
$$-\frac{1}{5}=\frac{3}{x-2}\Rightarrow x=-3\cdot5+2=-13$$
Задание 14591

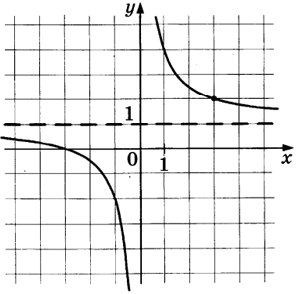
Точки $$(-4;-1)$$ и $$(-2;1)$$ принадлежат графику функции $$f(x).$$ Тогда:
$$\left\{\begin{matrix} -1=\frac{a-4k}{b-4}\\ 1=\frac{a-2k}{b-2} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a-4k=4-b\\ a-2k=-2+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 2a-6k=2\\ 2k=-6-2b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=3k+1\\ k=-3-b \end{matrix}\right.\Rightarrow b=-k-3$$
Точка $$(0;5)$$ принадлежит графику функции $$f(x).$$ Тогда:
$$\frac{a}{b}=5$$
$$a=5b$$
$$\left\{\begin{matrix} 3k+1=5b\\ b=-k-3 \end{matrix}\right.$$
$$3k+1=5(-k-3)$$
$$8k=-16$$
$$k=-2$$
Задание 14596

$$f(x)=\frac{kx+a}{x+b}=k+\frac{a-kb}{x+b}$$
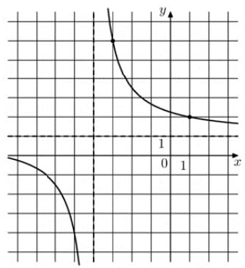
При этом $$b=-2,$$ так как вертикальная асимптота сдвинута на 2 единицы вправо.
Получим: $$f(x)=k+\frac{a+2k}{x-3}.$$
При этом $$k=-1,$$ так как горизонтальная асимптота сдвинута на 1 единицу вниз.
Получим: $$f(x)=-1+\frac{a-2}{x-3}.$$
График проходит через $$(-2;-2).$$
Получим: $$-2=-1+\frac{a-2}{-2-2}\Leftrightarrow -1=\frac{a-2}{-4}\Rightarrow a=6.$$
Задание 14621
График проходит через $$(4;-1)$$ и $$(2;-3)$$
Получим: $$\left\{\begin{matrix} -1=\frac{1}{4+a}+c\\ -3=\frac{1}{2+a}+c \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -c-1=\frac{1}{4+a}\\ -c-3=\frac{1}{2+a} \end{matrix}\right.$$
Вычтем из второго уравнения первое:
$$-2=\frac{1}{2+a}-\frac{1}{4+a}\Leftrightarrow -2=\frac{4+a-2-a}{(4+a)(2+a)}$$
$$-2(8+6a+a^2)=2\Leftrightarrow a^2+6a+8=-1\Leftrightarrow a^2+6a+9=0$$
$$\Rightarrow a=-3\Rightarrow -c-1=\frac{1}{4-3}\Rightarrow -c=1+1\Rightarrow c=-2$$
Задание 14875
Точки $$(2;1)$$ и $$(-4;-1)$$ принадлежат графику функции. Тогда:
$$\left\{\begin{matrix} \frac{k}{2+a}=1\\ \frac{k}{-4+a}=-1 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} k=2+a\\ k=4-a \end{matrix}\right.$$
$$2+a=4-a$$
$$2a=2$$
$$a=1$$
$$k=4-1=3$$
$$f(x)=\frac{3}{x+1}$$
$$f(19)=\frac{3}{19+1}=\frac{3}{20}=0,15$$
Задание 14894
График проходит через $$(1;-1); (3;1); (5;-5).$$ Получим:
$$\left\{\begin{matrix} -1=\frac{a\cdot1+b}{1+c}\\ 1=\frac{3a+b}{3+c}\\ -5=\frac{5a+b}{5+c} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -1-c=a+b\\ 3+c=3a+b\\ -25-5c=5a+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 4+2c=2a\\ 28+6c=-2a\\ 3+c=3a+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 32+8c=0\\ a=2+c\\ b=c+3-3a \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} c=-4\\ a=-2\\ b=5 \end{matrix}\right.$$
Получим: $$y=\frac{-2x+5}{x-4}.$$ Тогда $$f(29)=\frac{-2\cdot29+5}{29-4}=\frac{-53}{25}=-2,12$$
Задание 15049
Прямая проходит через $$(-2;-3)$$ и $$(0;5).$$ Получим:
$$\left\{\begin{matrix} -3=-2k+b\\ 5=0k+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -2k=-8\\ b=5 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} k=4\\ b=5 \end{matrix}\right.$$
Гипербола проходит через $$(-2;-3).$$ Тогда:
$$-3=\frac{k}{-2}\Rightarrow k=6.$$ Получим $$y=\frac{6}{x}.$$
$$\frac{6}{x}=4x+5\Leftrightarrow 4x^2+5x-6=0$$
$$D=25+96=121$$
$$x_1=\frac{-5+11}{2\cdot4}=\frac{1,5}{2}=0,75$$
$$x_2=\frac{-5-11}{2\cdot4}=-2$$
Задание 15068
График проходит через $$(-1;-1); (-2;0)$$ и $$(-4;-4).$$
Получим:
$$\left\{\begin{matrix} -1=\frac{a\cdot(-1)+b}{-1+c}\\ 0=\frac{a\cdot(-2)+b}{-2+c}\\ -4=\frac{a\cdot(-4)+b}{-4+c} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -1=\frac{b-a}{c-1}\\ 0=\frac{b-2a}{c-2}\\ -4=\frac{b-4a}{c-4} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 1-c=b-a\\ b-2a=0\\ 16-4c=b-4a \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 1-c=2a-a\\ b=2a\\ 16-4c-b=-4a \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} c=1-a\\ b=2a\\ 16-4+4a-2a=-4a \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=-2\\ b=-4\\ c=3 \end{matrix}\right.$$
Получим:
$$y=\frac{-2x-4}{x+3}.$$
$$y(17)=\frac{-34-4}{17+3}=\frac{-38}{20}=-1,9$$
Задание 15125
$$2=\frac{k}{3}+a$$
$$−2=\frac{k}{-1}+a$$
Решая систему, получаем:
$$f(x)=\frac{3}{x}+1$$
$$f(-12)=0,75$$
Задание 15302
График проходит через $$(1;2), (-3;6), (-5;-4).$$ Получим:
$$\left\{\begin{matrix} 2=\frac{k+a}{1+b}\\ 6=\frac{-3k+a}{-3+b}\\ -4=\frac{-5k+a}{-5+b} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 2+2b=k+a\\ -18+6b=-3k+a\\ 20-4b=-5k+a \end{matrix}\right.$$
Вычтем второе из первого и третьего:
$$\left\{\begin{matrix} 20-4b=4k\\ 38-10b=-2k \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 5-b=k\\ -19+5b=k \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 24-6b=0\\ 5-b=k \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=4\\ k=1 \end{matrix}\right.$$
Тогда:
$$2+2\cdot4=1+a\Rightarrow a=9$$