ЕГЭ Профиль
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1176
В равносторонний конус (диаметр основания конуса равен длине его образующей) вписан шар. Найдите отношение объема конуса к объему шара.
Объем конуса вычисляется по формуле:
$$V_{1}=\frac{1}{3}S*h=\frac{1}{3}\pi HB^{2}*AH$$
Объем шара вычисляется по формуле:
$$V_{2}=\frac{4}{3}\pi R^{3}=\frac{4}{3}\pi OH^{3}$$
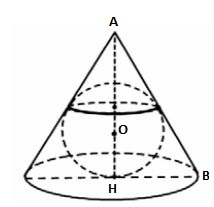
Дан равносторонний конус, то есть в осевом сечении будет равносторонний треугольник. Пусть AB = x, тогда HB = 0,5x и по теореме Пифагора из треугольника AHB: $$AH = \frac{\sqrt{3}}{2}x$$. OH - радиус вписанной в правильный треугольник окружности, и он равен 1/3 от высоты: $$OH = \frac{1}{3}AH = \frac{\sqrt{3}}{6}x$$
Значит объем конуса равен:
$$V_{1}=\frac{1}{3}S*h=\frac{1}{3}\pi (0.5x)^{2}* \frac{\sqrt{3}}{2}x$$
Объем шара равен:
$$V_{2}=\frac{4}{3}\pi R^{3}=\frac{4}{3}\pi (\frac{\sqrt{3}}{6}x)^{3}$$
Тогда:
$$\frac{V_{1}}{V_{2}}=\frac{\frac{1}{3}\pi (0.5x)^{2}* \frac{\sqrt{3}}{2}x}{\frac{4}{3}\pi (\frac{\sqrt{3}}{6}x)^{3}}$$
$$\frac{V_{1}}{V_{2}}=\frac{0.25x^{3}* \frac{\sqrt{3}}{2}}{ 4(\frac{\sqrt{3}}{6}x)^{3}}=2.25$$