ЕГЭ Профиль
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1278
В кубе с ребром, равным 3, сделано сквозное отверстие размером 1 х 1. Найдите площадь полной поверхности полученного многогранника.
Задание 2733
Найдите площадь поверхности многогранника (все двугранные углы прямые).
$$S=1\cdot3+1\cdot1+1\cdot2+1\cdot1+1\cdot1+1\cdot2+1\cdot2\cdot2+1\cdot2\cdot2=18$$
Задание 2939
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
$$S=2\cdot5+2\cdot5+2\cdot2+2\cdot2+5\cdot4+$$ $$+2\cdot6+2\cdot3+2\cdot3\cdot3+5\cdot3+$$ $$+5\cdot3+2\cdot3+5\cdot6=156$$
Задание 2986
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
При увеличении ребра в три раза, площадь каждой грани, а соответственно, и октаэдра, увеличится в 9 раз ( так как площади пободных фигур относятся как квадрат коэффициента подобия)
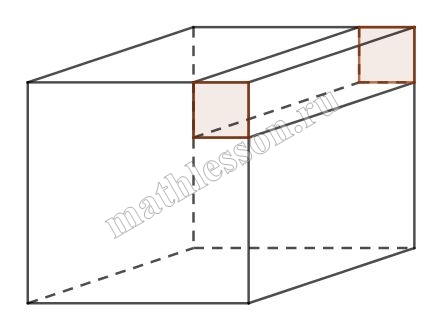
Задание 4955
Найдите площадь поверхности многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Для решения необходимо найти площади всех граней и сложить. Если "перенести" верхнюю грань куба, то можно рассматривать площадь поверхности начальной фигуры как сумму площадей поверхности нижнего параллелепипеда и боковой поверхности куба:
$$1\cdot2\cdot4+2\cdot2\cdot2+1\cdot1\cdot4=8+8+4=20$$
Задание 6414
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы — прямые).
В данном случае можно рассматривать фигуру, как параллелограмм (4*3*4), у которого вырезаны на передней и задней грани два квадрата со стороной 1.
Тогда площадь его поверхности составит: $$S=4*4*2+4*3*4-1*1*1=32+48-2=78$$
Задание 6693
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Рассмотрим куб со стороной 3 и параллели 1;5;5 . Если из их площади поверхности вычесть 2 раза по 3*3 , то получим площадь поверхности исходной фигуры: $$S=3*3*6+1*5*2+1*5*2+5*5*2-3*3*2=106$$
Задание 6819
Из куба с ребром 3 вырезана правильная четырёхугольная призма со стороной основания 2,5 и боковым ребром 3. Найдите площадь поверхности получившегося после вырезания многогранника.
Площадь поверхности куба, с учетом вырезов в основаниях: $$3*3*6-2,5*2,5*2=54-12,5=41,5$$
Площадь внутренней поверхности: $$2,5 *3*4=30$$
Площадь поверхности многогранника: $$41,5+30=71,5$$
