ЕГЭ Профиль
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1011
Ответ: 2
Скрыть
|
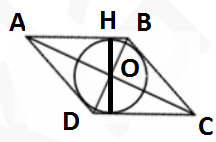
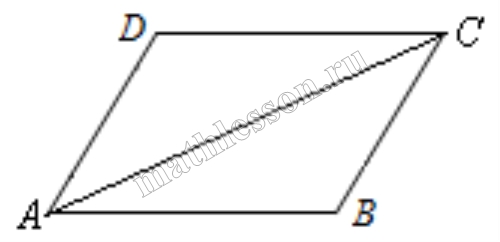
Площадь ромба вычисляется как половина произведения диагоналей. То есть $$S = 0.5 *2\sqrt{5}*4\sqrt{5}=20$$ С другой стороны, площадь равна произведению основания на высоту, а высота равна двум радиусам вписанной окружности. То есть S = AB * 2 OH = AB * 2r Найдем AB по теореме Пифагора из треугольника ABO (его катеты равны половинам диагоналей): $$AB = \sqrt{\sqrt{5}^{2}+2\sqrt{5}^{2}}=\sqrt{5+20}=5$$ Приравняем площади: 20 = 5 * 2r, r = 2 |