ЕГЭ Профиль
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 901
На графике производной функции у = f ' / (x) отмечены семь точек: х1,…, х7. Найдите все отмеченные точки, в которых функция f (x) возрастает. В ответе укажите количество этих точек.
| Так как дан график производной, то мы будем искать точки над осью OX (функция возрастает, производная положительна) |
Задание 937
На графике производной функции у = f' / (x) отмечены семь точек: х1,…, х7. Найдите все отмеченные точки, в которых угловой коэффициент касательной к графику функции f (x) положительный. В ответе укажите количество этих точек.
Угловой коэффициент касательной к графику это и есть значение производной, следовательно, мы ищем, где производная положительная. Так как дан нам график производной, то мы просто найдем количество точек, которые располагаются над осью ОХ: x1,x3,x4,x6 всего 4
Задание 1013
Производная непрерывной функции f (x) равна нулю в каждой точке отрезка [‐5; 4]. Известно, что f (– 5) = – 5. Найдите f (4)
Раз производная равна нулю на всем промежутке и функция непрерывна, то функция не возрастает и не убывает, то есть сохраняет свое значение. Значит f(– 5) =f(4)= – 5
Задание 1175
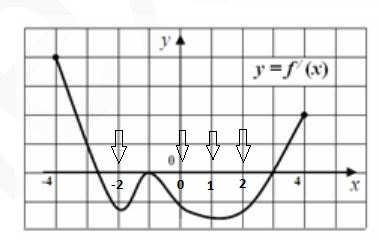
Функция у = f (x) определена на отрезке [‐4; 4]. На рисунке приведен график её производной. Найдите промежутки убывания функции. В ответе укажите сумму всех целых x, входящих в эти промежутки.
Функция убывает, когда производная отрицательная. То есть мы смотрим, где график производной лежит под осью оХ, и выбираем оттуда целые значения Х (в задании надо сумму целых чисел). Важно выбрать значения, где производная равна 0, так как считается, что если функция определена в точках максимума или минимума, то эти точки входят в промежутки возрастания и убывания. Получаем точки -2; -1; 0 ; 1 ; 2 ;3
-2-1+0+1+2+3=3
Задание 2350
На рисунке изображен график $$y={f}'(x)$$ – производной функции f (x), определенной на интервале (‐6; 5). Найдите точку экстремума функции f (x), принадлежащую отрезку [-5; 4]

| Точка экстремума там, где производная равна 0. Т. к. нам дан график производной, то она равна 0 там, где пересекает ось Ох, т. е. в точке -2. |  |
Задание 2784
На рисунке изображён график $$y={f}'x$$ – производной функции f (x). На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7 . Сколько из этих точек лежит на промежутках возрастания функции f (x)?
Промежутки возрастания функции там, где график производной над осью Ox: x1; x2 $$\Rightarrow$$ 2 точки.
Задание 2860
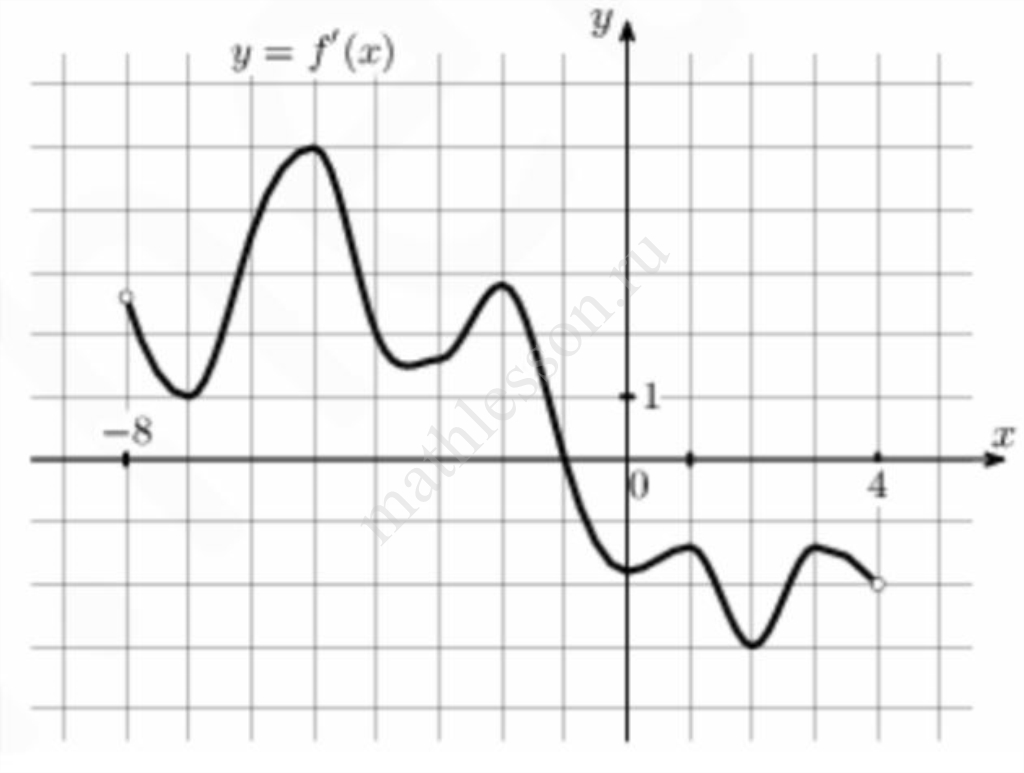
На рисунке изображён график y=f′(x) — производной функции f(x), определенной на интервале (-8;4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение?
На всем отрезке [-7; -3] f'(x) $$\Rightarrow$$ функция возрастает минимальное значение в начале отрезка $$\Rightarrow$$ -7
Задание 2938
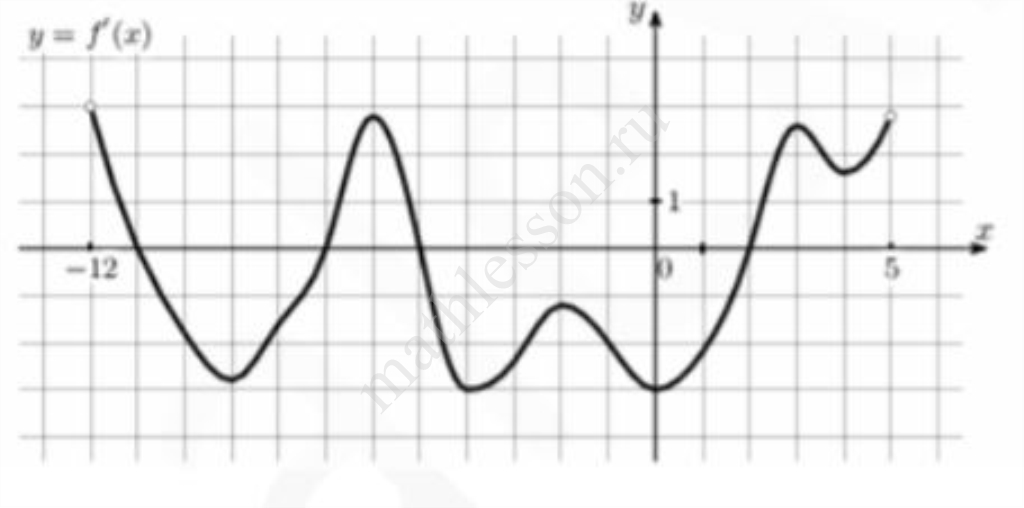
На рисунке изображен график y=f′(x) - производной функции f(x), определенной на интервале (-12;5). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-10;4].
$$-7; 2$$ $$\Rightarrow$$ 2 точки
Задание 2985
На рисунке изображен график функции y=f(x), определенной на интервале (−6;8). Определите количество целых точек, в которых производная функции положительна.
Производная положительная в том случае, когда функция возрастает. Целые абсциссы на графики, где функция возрастает отмечены жирными точками. Их 4

Задание 3111
Функция у = f (x) определена на отрезке [-2; 4]. На рисунке приведен график ее производной. Укажите абсциссу точки графика функции у = f (x), в которой она принимает наименьшее значение.
Производная $$>0$$ $$\Rightarrow$$ f всегда возрастает $$\Rightarrow$$ в начале промежутка
Задание 3283
На рисунке изображен график производной функции y=f′(x), определенной на интервале (−3;9). Найдите промежутки возрастания функции. В ответе укажите сумму целых точек, входящих в эти промежутки.
Раз изображен график производной, то мы должны смотреть промежутки, где этот график находится над осью Ох (так как функция возрастает тогда, когда значение производной положительно). На этих промежутках абсциссы (координаты Х) целые: -2 ; -1 ; 4 ; 5 ; 6 ; 7 (-2) + (-1) + 4 + 5 + 6 + 7 = -3 + 22 = 19
Задание 3370
На рисунке изображен график $$y=f'(x)$$ – производной непрерывной функции $$f(x)$$ , определенной на интервале (-4; 7). Найдите количество точек минимума функции $$f(x)$$ , принадлежащих отрезку [-3; 6].
Первая точка, когда график пересекает ось Ох в точке -2 (значение производной было отрицательным, стало положительным), вторая в точке 2, так как функция по условию непрерывна, а значение производной до этого было отрицательным, значит в этой точке хоть производная и не найдена, но значение функции минимальное на отрезке) и третья в точке 5.
Задание 3418
На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (- 8; 4). В какой точке отрезка [- 2; 3] функция f(x) принимает наименьшее значение?
На отрезке [- 2; 3] везде $$f'(x)>0$$ $$\Rightarrow$$ $$f(x)$$ везде возрастает $$\Rightarrow$$ $$f_{min}$$ в начале отрезка, т.е. в т. -2