ЕГЭ Профиль
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
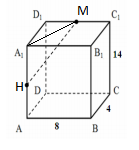
Задание 938
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно ВС=4, АВ=8, СС1=14. Найдите расстояние между серединами ребер АА1 и С1D1.
|
Для этого рассмотрим треугольник HA1M: HA1=0.5AA1=7 A1M=$$\sqrt{A_{1}D_{1}^{2}+D_{1}M^{2}}=\sqrt{4^{2}+4^{2}}=\sqrt{32}$$ MH=$$\sqrt{A_{1}H^{2}+A_{1}M^{2}}=\sqrt{7^{2}+32}=\sqrt{81}=9$$ |
Задание 2824
Объем параллелепипеда ABCDA1B1C1D1 равен 9. Найдите объем треугольной пирамиды АВDА1.
$$S_{ABCDA_{1}B_{1}C_{1}D_{1}}=S_{ABCD}\cdot h$$ $$S_{ABDA_{1}}=\frac{1}{3}\cdot S_{ABD}\cdot h=\frac{1}{3}\cdot \frac{1}{2}\cdot S_{ABCD}\cdot h=\frac{9}{6}=1,5$$
Задание 2861
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Пусть х - третье ребро $$2\cdot3x+2\cdot4x+2\cdot3\cdot4=94$$ $$6x+8x+24=94$$ $$\Leftrightarrow$$ $$14x=70$$ $$\Leftrightarrow$$ $$x=5$$
Задание 3029
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 6. Диагональ параллелепипеда равна 9. Найдите площадь поверхности параллелепипеда.
$$3^{2}+6^{2}+x^{2}=9^{2}$$ $$9+36+x^{2}=81$$ $$x^{2}=36$$ $$x=6$$ $$S=2\cdot3\cdot6+2\cdot3\cdot6+2\cdot6\cdot6=36+36+72=144$$
Задание 3656
В основании прямоугольного параллелепипеда лежит квадрат с площадью, равной 18. Найдите диагональ параллелепипеда, если известно, что его боковое ребро равно 8.
1) Пусть $$AB=BC=x$$: $$S_{ABCD}=x^{2}=18$$
2) $$BD^{2}=AB^{2}+AD^{2}=2x^{2}$$
3) $$B_{1}D=\sqrt{BD^{2}+BB_{1}^{2}}=\sqrt{2\cdot18+64}=\sqrt{100}=10$$