Тригонометрические уравнения, исследование ОДЗ

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

a) ОДЗ: $$\left\{\begin{matrix}\sin2x\geq0\\\cos x\geq0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}2\pi n\leq2x\leq\pi+2\pi n\\-\frac{\pi}{2}+2\pi n\leq x\leq\frac{\pi}{2}+2\pi n\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}\pi n\leq x\leq\frac{\pi}{2}+\pi n\\-\frac{\pi}{2}+2\pi n\leq x\leq\frac{\pi}{2}+2\pi n\end{matrix}\right.$$

$$x\in[2\pi n;\frac{\pi}{2}+2\pi n]\cup{-\frac{\pi}{2}+2\pi n},n\in Z$$

$$\sin2x=\sqrt{2}\cos x$$; $$2\sin x\cos x-\sqrt{2}\cos x=0$$; $$\sqrt{2}\cos x(\sqrt{2}-1)=0$$; $$\left\{\begin{matrix}\cos x=0\\\sin x=\frac{\sqrt{2}}{2}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{\pi}{2}+\pi n\\x=(-1)^{n}\frac{\pi}{4}+\pi n,n\in Z\end{matrix}\right.$$ 

С учетом ОДЗ: $$\frac{\pi}{2}+2\pi n;\frac{\pi}{4}+2\pi n,n\in Z$$

б) $${-\frac{3\pi}{2};-\frac{\pi}{2}}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

A)     $$\frac{1}{\cos 2x *\cos x}=\frac{1}{\sin 2x*\sin x}$$

Найдем область определения:

$$\left\{\begin{matrix}\cos 2x\neq 0 \\\cos x \neq 0 \\\sin 2x \neq 0 \\\sin x \neq 0 \end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}x \neq \frac{\pi}{4}+\frac{\pi n}{2} \\x \neq \frac{\pi}{2}+\pi n \\x \neq \frac{\pi n }{2} \\x \neq \pi n \end{matrix}\right.\Leftrightarrow$$ $$x \neq \frac{\pi n}{4}, n \in Z$$

$$\cos 2x*\cos x=\sin 2x*\sin x\Leftrightarrow$$$$(\cos^{2}x-\sin^{2}x)\cos x-2 \sin x\cos x\sin x=0\Leftrightarrow$$$$\cos^{3}x-\sin^{2}x\cos x-2 \sin^{2}x \cos x=0\Leftrightarrow$$$$\cos^{3}x-3\sin^{2}x \cos x=0\Leftrightarrow$$$$\cos x(\cos^{2}x-3 \sin ^{2}x)=0$$

$$\left\{\begin{matrix}\cos x=0 \\1-\sin^{2}x-3 \sin^{2}x=0 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{\pi}{2}+\pi n , n \in Z \notin (1) \\\sin ^{2}x=\frac{1}{4} \end{matrix}\right.\Leftrightarrow$$$$\sin x=\pm \frac{1}{2}\Leftrightarrow$$$$\left\{\begin{matrix}x=(-1)^{n}\frac{\pi}{6}+\pi n, n \in Z \\x=(-1)^{n+1}\frac{\pi}{6}+\pi n, n \in Z \end{matrix}\right.$$

Б)     Начертим единичную окружность, отметим заданный промежуток и полученные корни.

Видим, что в заданный промежуток попали:

$$\frac{\pi}{6}+2\pi n$$:$$-2\pi+\frac{\pi}{6}=-\frac{11\pi}{6}$$

$$\frac{5\pi}{6}+2\pi n$$:$$-\pi-\frac{\pi}{6}=-\frac{7\pi}{6}$$

$$-\frac{5\pi}{6}+2\pi n$$:$$-\pi+\frac{\pi}{6}=-\frac{5\pi}{6}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

а)$$(1+tg^{2}x)*\cos(\frac{\pi }{2}+2x)=\frac{2}{\sqrt{3}}$$

Найдем ограничения по х:

$$\cos x\neq 0\Leftrightarrow x+\frac{\pi }{2}+\pi *n, n\in Z$$

Учтем, что $$1+tg^{2}x=\frac{1}{\cos^{2}x}$$ и $$\cos(\frac{\pi }{2}+2x)=-\sin 2x$$

$$\frac{1}{\cos^{2}x}*(-\sin 2x)=\frac{2}{\sqrt{3}}$$

Воспользуемся формулой синуса двойного угла:

$$\frac{-2*\sin x*\cos x}{cos^{2}x}=\frac{2}{\sqrt{3}}$$ $$-tgx=\frac{1}{3}$$

$$tg x=-\frac{\sqrt{3}}{3}$$ $$x=-\frac{\pi }{6}+\pi *n, n\in Z$$

б)Отметим полученные корни в общем виде на окружности, а так же интервал, данный по условию (он включает в себя полностью всю окружность (синий цвет) и сектор во второй четверти (красный цвет))

Найдем корни, которые попадут в данный промежуток:

$$-\pi -\frac{\pi }{6}=-\frac{7\pi }{6}$$

$$0-\frac{\pi }{6}=-\frac{\pi }{6}$$

$$\pi -\frac{\pi }{6}=\frac{5\pi }{6}.$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

а) $$\frac{4 \cos x-5}{2 \cos x -1}+\frac{1}{2 cos^{2}x-\cos x}=2|*(2 \cos^{2} x-\cos x)$$

Найдем ограничение по y:

$$\left\{\begin{matrix}2 \cos x-1\neq 0 \\2 \cos^{2} x-\cos x\neq 0\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}\cos \neq \frac{1}{2} \\\cos x(2 \cos x-1)\neq 0\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}\cos x\neq \frac{1}{2}\\\cos x\neq 0\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}x\neq \pm \frac{\pi }{3}+2\pi n\\x\neq \frac{\pi }{2}+\pi n,n\in Z\end{matrix}\right.$$

$$(4 \cos x-5) \cos x+1=2(2 \cos^{2 }x -\cos x)$$

$$4 \cos^{2}x -5 \cos x+1-4 \cos^{2}x+2 \cos x=0$$

$$-3 \cos x+1=0$$

$$\cos x=\frac{1}{3}\Leftrightarrow$$$$x\pm \arccos\frac{1}{3}+2\pi n, n\in Z$$

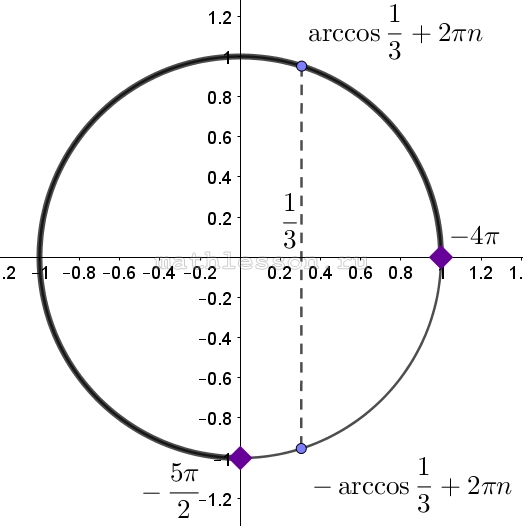
б) Отметим полученные корни, заданный промежуток на единичной окружности:

Как видим один корень попадает в заданный промежуток. Найдем его частный случай: $$-4\pi+\arccos \frac{1}{3}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

   А) $$\frac{ctg x -tg x}{3 \sin x +\cos 2x}=ctg 2x$$

Область определения D(f): $$\left\{\begin{matrix}3 \sin x+\cos 2x\neq 0 \\\sin x \neq 0 \\\cos x\neq 0 \\\sin 2x\neq 0 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}1-2\sin ^{2}x+3 \sin x\neq 0 (1)\\x\neq \frac{\pi n }{2} n\in Z\end{matrix}\right.$$

(1)$$2 \sin^{2}x -3 \sin x-1\neq 0$$

$$D=9+8=17$$

$$\left\{\begin{matrix}\sin x \neq\frac{3+\sqrt{17}}{4} \\\sin x \neq \frac{3-\sqrt{17}}{4} \end{matrix}\right.$$

Решим данное уравнение:

$$\frac{\frac{\cos x }{\sin x}-\frac{\sin x}{\cos x}}{1+3 \sin x-2 \sin^{2}x}=\frac{\cos ^{2}x-\sin^{2}x}{2\sin x *\cos x}$$

$$\frac{\cos^{2}x-\sin^{2}x}{\sin x \cos x(1+3\sin x-2 \sin ^{2})}=\frac{\cos ^{2}x-\sin^{2}x}{2 \sin x \cos x}$$

$$\frac{\cos 2x}{\sin 2x}(\frac{1}{1+3 \sin x-2 \sin ^{2}}-\frac{1}{2})=0$$

$$\left\{\begin{matrix}ctg 2x=0 \\1+3 \sin x-2 \sin^{2}x -2=0 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}2x=\frac{\pi}{2}+\pi n , n \in Z \\2 \sin^{2} x-3 \sin x+1=0(2) \end{matrix}\right.$$

(2)$$2 \sin^{2}x -3 \sin x+1= 0$$

$$D=9+8=1$$

$$\left\{\begin{matrix}\sin x =\frac{3+1}{4}=1 \notin D(f) \\\sin x=\frac{3-1}{4}=\frac{1}{2} \end{matrix}\right.$$

     Б) Найдем данный промежуток на единичной окружности (розовым выделен) и отметим общий вид корней. Найдем корни, которые попали на жанный промежуток:

     1)Найдем корни вида $$(-1)^{n}\frac{\pi}{6}+2\pi*n(2)$$ : $$-\pi-\frac{\pi}{6}=-\frac{7\pi}{6}$$

     2) Найдем корни вида $$\frac{\pi*n}{4}$$:

$$(2)-\pi-\frac{\pi}{4}=-\frac{5\pi}{4}$$ ; 

$$(3)-\pi+\frac{\pi}{4}=-\frac{3\pi}{4}$$ ; 

$$(4)0-\frac{\pi}{4}=-\frac{\pi}{4}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

A)     Найдем область определения D(f):

$$\left\{\begin{matrix}4+3 \cos x-\cos 2x\geq 0(1) & & \\\sin x\geq 0(2) & &\end{matrix}\right.$$

     Рассмотрим первое неравенство системы $$(1): 2 \cos ^{2}x-1-3 \cos x-4\leq 0$$

$$2 \cos ^{2}x-3 \cos x-5\leq 0$$

$$D=9+40=49$$

$$\cos x=\frac{3+7}{4}=2,5$$

$$\cos x=\frac{3-7}{4}=-1$$

$$\left\{\begin{matrix}\cos x\geq -1\\\cos x\leq 2,5 \end{matrix}\right.\Leftrightarrow$$ $$x \in R$$

     Рассмотрим второе неравенство системы $$(2): \sin x\geq 0 \Leftrightarrow x\in [2\pi n, \pi+2\pi n], n \in Z$$

     Решим данное уравнение:

$$5+3 \cos x-2 \cos^{2}x=6\sin ^{2}x=6-6 \cos ^{2}$$

$$4 \cos ^{2}+3 \cos x-1=0$$

$$D=9+16=25$$

$$\left[\begin{matrix}\cos x=\frac{-3+5}{8}=\frac{1}{4}\\\cos x=\frac{-3-5}{8}=-1\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=arccos \frac{1}{4}+2\pi n\\x=-arccos\frac{1}{4}+2 \pi n \notin D(f)\\x=-\pi+2 \pi k, k\in Z\end{matrix}\right.$$

Б)     Найдем корни на заданном промежутке

Как видим корень (1) не попадает в заданный промежуток а корень (3) попадает. Найдем его: $$-\frac{7\pi}{2}+\frac{\pi}{2}=-3\pi.$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

А)   $$\frac{2+\cos 4x-8\cos^{4}x }{4(\cos x+\sin x)}=\frac{1}{\sin x}$$

     Область определения D: $$\left\{\begin{matrix}\cos x+\sin x \neq 0\\\ \sin x\neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}tg x\neq -1\\x\neq \pi n , n \in Z\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix} x\neq -\frac{\pi}{4}+\pi n\\x\neq \pi n\end{matrix}\right.$$

     Рассмотрим числитель первой дроби:

$$\cos 4x=2 \cos^{2}2x-1=$$$$2(2 \cos ^{2}x-1)^{2}-1=2(4\cos ^{4}x-4\cos ^{2}x+1)=$$$$8\cos^{4}x-8 \cos ^{2}x+1=$$$$3+8\cos^{4}x-8 \cos ^{2}x+1-8\cos ^{4}x=4-8\cos ^{2}x$$

     Выполним преобразования:

$$\frac{4(1-2\cos^{2}x)}{4(\cos x+\sin x)}=\frac{1}{\sin x}\Leftrightarrow$$$$\frac{1-2 \cos ^{2}x}{\cos x+\sin x}=\frac{1}{\sin x}\Leftrightarrow$$$$\sin x-2 \cos^{2}x*\sin x=\cos x+\sin x\Leftrightarrow$$$$\cos x+2 \cos^{2}x \sin x=0\Leftrightarrow$$$$\cos x(1+2\cos x \sin x)=0\Leftrightarrow$$

     Произведение равно нулю, когда хотя бы один из множителей равен нулю: 

$$\left[\begin{matrix}\cos x=0\\1+\sin 2x=0\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\frac{\pi}{2}+\pi n\\2x=-\frac{\pi}{2}+2\pi n\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\frac{\pi}{2}+\pi n\\x=-\frac{\pi}{4}+\pi n\notin D\end{matrix}\right.$$

Б)   Найдем корни, принадлежащие данному промежутку: $$\pi\approx 3,14\Rightarrow$$ $$\frac{\pi}{2}\approx 1,57$$. Тогда $$\frac{\pi}{2}+\pi=\frac{3 \pi}{2}\in [2 ;5]$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

A)   Область определения D(x):

$$\left\{\begin{matrix}2\cos x-1\neq 0\\2 \cos ^{2}x-\cos x\neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\cos x=\frac{1}{2}\\\cos x\neq 0\end{matrix}\right.$$

$$\frac{2\cos x-3}{2\cos x-1}+\frac{1}{\cos x(2 \cos x-1)}=0$$

     Приведем к общему знаменателю и приравняем числитель к нулю:

$$2 \cos^{2}x-3\cos x+1=0$$

     Пусть $$\cos x=t \in [-1 ;1]$$

$$2t^{2}-3t+1=0$$

$$D=9-8=1$$

$$t_{1}=\frac{3+1}{4}=1$$

$$t_{2}=\frac{3-1}{4}=\frac{1}{2}$$

     Тогда : $$\left\{\begin{matrix}\cos x=1\\\cos x=\frac{1}{2}\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=2\pi n , n \in Z\\\notin D(x)\end{matrix}\right.$$

Б)   На данном промежутке при n=-2 получаем $$x=-4\pi$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     ОДЗ: $$\cos 3x\neq 0\Leftrightarrow$$ $$3x\neq \frac{\pi}{2}+\pi n,n \in Z\Leftrightarrow$$$$x\neq \frac{\pi}{6}+\frac{\pi}{3}, n\in Z$$

     Рассмотрим левую часть уравнения:

$$\sin^{2}2x+\sin ^{2}4x=$$$$\sin^{2}2x+ (2\sin 2x\cos 2x)^{2}=$$$$\sin^{2}2x(1+4\cos^{2}2x)=$$$$(1-\cos ^{2}2x)(1+4\cos ^{2}2x)=$$$$1+3\cos ^{2}2x-4 \cos^{4}2x$$

     Подставим полученное выражение в уравнение:

$$1+3\cos^{2}2x-4\cos^{4}2x=1-\frac{\cos 2x}{\cos 3x}\Leftrightarrow$$$$4\cos ^{4}2x-3\cos ^{2}2x=\frac{\cos 2x}{\cos 3x}\Leftrightarrow$$$$\cos 2x(4\cos^{3}2x-3 \cos 2x)=\frac{\cos 2x}{\cos 3x}\Leftrightarrow$$$$\cos 2x*\cos 6x-\frac{\cos 2x}{\cos 3x}=0\Leftrightarrow$$$$\cos 2x(\cos 6x-\frac{1}{\cos 3x})=0$$

     Произведение равно 0, когда хотя бы один из множителей равен 0:

$$\left[\begin{matrix}\cos 2x=0\\\cos 6x-\frac{1}{\cos 3x}=0\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}2x=\frac{\pi}{2}+\pi n \Rightarrow x=\frac{\pi}{4}+\frac{\pi n }{2}\\(-1+2\cos^{2}3x)-\frac{1}{\cos 3x}=0(2)\end{matrix}\right.$$

     Рассмотрим уравнение (2):$$2\cos ^{2}3x-1-\frac{1}{\cos 3x}=0$$, пусть $$\cos 3x=y$$, тогда: $$\frac{2y^{3}-y-1}{y}=0\Leftrightarrow$$$$(y-1)(2y^{2}+2y+1)=0$$. Так как вторая скобка всегда положительна, то: $$y=1\Leftrightarrow$$$$\cos 3x=1\Leftrightarrow 3x=2\pi n \Leftrightarrow x=\frac{2\pi n }{3}, n \in Z$$

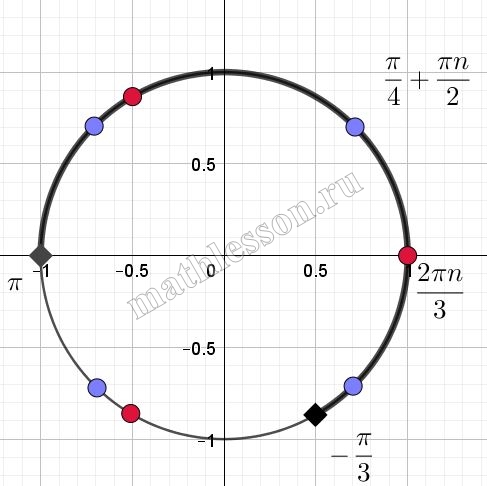
   Б) Отметим полученные корни и промежуток на единичной окружности, найдем корни:

Для $$\frac{2\pi n}{3}$$ (красный цвет): $$0;\frac{2\pi}{3}$$

Для $$\frac{\pi}{4}+\frac{\pi n}{3}$$ (синий цвет): $$-\frac{\pi}{4};\frac{\pi}{4};\frac{3\pi}{4}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

   А) $$\frac{\cos 2x-\cos 4x-4\sin 3x-2\sin x+4}{2\sin x-1}=0\Leftrightarrow$$ $$\left\{\begin{matrix}\cos 2x-\cos 4x-4\sin 3x-2\sin x+4=0\\2\sin x\neq 1\end{matrix}\right.$$

     Рассмотрим первое условие полученной системы. $$2\sin x \sin 3x-4 \sin 3x-2 \sin x+4=0\Leftrightarrow$$ $$\sin 3x(\sin x-2)-(\sin x-2)=0\Leftrightarrow$$ $$(\sin 3x-1)(\sin x-2)=0$$

     Поскольку $$\left | \sin x \right |\leq 1$$, остаётся только уравнение : $$\sin 3x-1=0$$, откуда $$x=\frac{\pi}{6}+\frac{2\pi}{3}n$$.

     Сравним решения второго условия системы с полученными решениями: $$\frac{\pi}{6}+\frac{2\pi}{3}n\neq \frac{\pi}{6}+2\pi k\Rightarrow$$ $$n\neq 3k,k \in Z$$ и $$\frac{\pi}{6}+\frac{2\pi}{3}n\neq \frac{5\pi}{6}+2\pi k\Rightarrow$$ $$n\neq 1+3k,k\in Z$$

     Таким образом ,остаются только те решения первого уравнения , для которых $$n=3k-1$$: $$x=\frac{\pi}{6}+\frac{2\pi*(3k-1)}{3}=-\frac{\pi}{6}+2\pi k$$

   Б) $$-\pi\leq -\frac{\pi}{2}+2\pi k<\frac{3\pi}{2}\Leftrightarrow$$ $$-\frac{1}{4}\leq k<1\Leftrightarrow$$ $$k=0\Rightarrow$$ $$x=-\frac{\pi}{2}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

   А) $$\sqrt{2\cos^{2} x-\sqrt{2}}+\sqrt{2}\sin x=0\Leftrightarrow$$$$\sqrt{2\cos^{2} x-\sqrt{2}}=-\sqrt{2}\sin x$$

     ОДЗ:  $$\left\{\begin{matrix}2\cos^{2}x\geq \sqrt{2}\\-\sqrt{2}\sin x\geq 0\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}\cos x \in (-\infty;-\frac{1}{\sqrt[4]{2}}]\cup[\frac{1}{\sqrt[4]{2}};+\infty)\\\sin x\leq 0\end{matrix}\right.$$

     Возведем обе части в квадрат: $$2\cos^{2} x-\sqrt{2}=2\sin^{2}x$$

     Применим формулы понижения степени: $$1+\cos 2x -\sqrt{2}=1-\cos 2x\Leftrightarrow$$$$2\cos 2x=\sqrt{2}\Leftrightarrow$$$$\cos 2x=\sqrt{2}{2}\Leftrightarrow$$$$2x=\pm \frac{\pi}{4}+2\pi n,n \in Z\Leftrightarrow$$$$x=\pm \frac{\pi}{8}+\pi n,n \in Z$$

     С учетом ОДЗ (синус меньше или равен 0): $$x_{1}=-\frac{\pi}{8}+\pi n,n \in Z$$ и $$x_{2}=-\frac{7\pi}{8}+\pi n,n \in Z$$

   Б) На заданном промежутке: 

$$x_{2}: -7\pi + \frac{\pi}{8}=-\frac{55\pi}{8}$$

$$x_{1}: -6\pi -\frac{\pi}{8}=-\frac{49\pi}{8}$$