ОГЭ
Задание 1652
О числах a и b известно, что a>b . Среди приведенных ниже неравенств выберите верные:
В ответе укажите номер правильного варианта.
- $$a-b< -3$$
- $$b-a> 1$$
- $$b-a< 2$$
- Верно 1,2 и 3
Пусть $$a=2, b=1$$ (подобрали числа, чтобы выполнялось неравенство a>b). Проверим правильность представленных вариантов:
- $$a-b< -3\Leftrightarrow$$$$2-1< -3\Leftrightarrow$$$$1< -3$$ - неверно
- $$b-a> 1\Leftrightarrow$$$$1-2> 1\Leftrightarrow$$$$-1>1$$ - неверно
- $$b-a< 2\Leftrightarrow$$$$1-2< 2\Leftrightarrow$$$$-1< 2$$ - верно
- Верно 1,2 и 3
Верным оказался только третий вариант
Задание 1653
На координатной прямой изображены числа а и с. Какое из следующих неравенств неверно?
- $$a-1>c-1$$
- $$-a<-c$$
- $$\frac{a}{6}<\frac{c}{6}$$
- $$a+3>c+1$$
Подберем любые значения a и b, чтобы выполнялось неравенство, предаставленное на рисунке (a>c). Пусть $$a=2, c=1$$. Проверим истинность представленных вариантов:
- $$a-1>c-1\Leftrightarrow$$$$2-1>1-1\Leftrightarrow$$$$1>0$$ - верно
- $$-a<-c\Leftrightarrow$$$$-2<-1$$ - верно
- $$\frac{a}{6}<\frac{c}{6}\Leftrightarrow$$$$\frac{2}{6}<\frac{1}{6}$$ - неверно
- $$a+3>c+1\Leftrightarrow$$$$2+3>1+1\Leftrightarrow$$$$5>2$$ - верно
Неверным является вариант под номером 3
Задание 1654
Какое из следующих неравенств не следует из неравенства $$y-x>z$$?
В ответе укажите номер правильного варианта.
- $$y>z+x$$
- $$y-x-z<0$$
- $$z+x-y<0$$
- $$y-z>x$$
Выполним преобразования с каждым из представленных вариантов:
- $$y>z+x|-x\Leftrightarrow$$$$y-x>z$$ - получили первоначальное неравенство
- $$y-x-z<0|+z\Leftrightarrow$$$$y-x<z$$ - не получили первоначальное неравенство
- $$z+x-y<0|-z|*(-1)\Leftrightarrow$$$$y-x>z$$ - получили первоначальное неравенство
- $$y-z>x|-x+z\Leftrightarrow$$$$y-x>z$$ - получили первоначальное неравенство
Не получили только во втором варианте ответа
Задание 1655
Известно, что $$a>b>0$$. Какое из указанных утверждений верно?
В ответе укажите номер правильного варианта.
- $$2a+1<0$$
- $$-a>-b$$
- $$2b>2a$$
- $$1-a<1-b$$
Пусть $$a=2, b=1$$ (подобрали числа, чтобы выполнялось неравенство a>b>0). Проверим правильность представленных вариантов:
- $$2a+1<0\Leftrightarrow$$$$2*2+1<0\Leftrightarrow$$$$5<0$$ - неверно
- $$-a>-b\Leftrightarrow$$$$-2>-1$$ - неверно
- $$2b>2a\Leftrightarrow$$$$2*1>2*2\Leftrightarrow$$$$2>4$$ - неверно
- $$1-a<1-b\Leftrightarrow$$$$1-2<1-1\Leftrightarrow$$$$-1<0$$ - верно
Верным оказался только 4 вариант ответа
Задание 1656
На координатной прямой отмечено число а. Какое из утверждений относительно этого числа является верным?
В ответе укажите номер правильного варианта.
- $$a+4>0$$
- $$a+5<0$$
- $$2-a>0$$
- $$3-a<0$$
Выберем значение а в соответствии с представленным рисунком: $$-5<a<-4$$. Пусть $$a=-4,5$$. Проверим верность представлнных утверждений:
- $$a+4>0\Leftrightarrow$$$$-4,5+4>0\Leftrightarrow$$$$-0,5>0$$ - неверно
- $$a+5<0\Leftrightarrow$$$$-4,5+5<0\Leftrightarrow$$$$0,5<0$$ - неверно
- $$2-a>0\Leftrightarrow$$$$2-(-4,5)>0\Leftrightarrow$$$$6,5>0$$ - верно
- $$3-a<0\Leftrightarrow$$$$3-(-4,5)<0\Leftrightarrow$$$$7,5<0$$ - неверно
Верным оказался только третий вариант ответа
Задание 1658
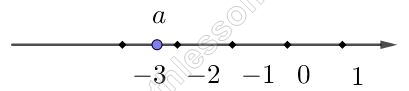
На координатной прямой отмечено число а. Какое из утверждений относительно этого числа является верным?
В ответе укажите номер правильного варианта.
- $$-a<2$$
- $$-1-a>0$$
- $$\frac{1}{a}>0$$
- $$a+3<0$$
Выберем значение а в соответствии с условием задачи: $$-3<a<-2$$. Пусть $$a=-2,5$$. Проверим истинность представленных варинатов:
- $$-a<2\Leftrightarrow$$$$-(-2,5)<0\Leftrightarrow$$$$2,5<0$$ - неверно
- $$-1-a>0\Leftrightarrow$$$$-1-(-2,5)>0\Leftrightarrow$$$$1,5>2$$ - верно
- $$\frac{1}{a}>0\Leftrightarrow$$$$\frac{1}{-2,5}>0\Leftrightarrow$$$$-0,4>0$$ - неверно
- $$a+3<0\Leftrightarrow$$$$-2,5+3<0\Leftrightarrow$$$$0,5<0$$ - неверно
Верным оказался только 2 вариант ответа
Задание 1663
На координатной прямой отмечены числа a, b, и c.
В ответе укажите номер правильного варианта.
- $$a+b>0$$
- $$\frac{1}{b}>\frac{1}{c}$$
- $$ab<0$$
- $$(a-b)c<0$$
Подберем числа a, b и c в соответствии с условиями задачи: $$a<b<0<c$$. Пусть $$a=-2 ; b=-1 ; c=1,5$$. Проверим истинность представленнх вариантов ответов:
- $$a+b>0\Leftrightarrow$$$$-2+(-1)>0\Leftrightarrow$$$$-3>0$$ - неверно
- $$\frac{1}{b}>\frac{1}{c}\Leftrightarrow$$$$\frac{1}{-1}>\frac{1}{1}\Leftrightarrow$$$$-1>1$$ - неверно
- $$ab<0\Leftrightarrow$$$$(-2)*(-1)<0\Leftrightarrow$$$$2<0$$ - неверно
- $$(a-b)c<0\Leftrightarrow$$$$(-2-(-1))*1<0\Leftrightarrow$$$$-1<0$$ - верно
Верным является только вариант под номером 4
Задание 1664
На координатной прямой отмечены числа a и b?
Какое из следующих чисел наибольшее?
- $$a+b$$
- $$-a$$
- $$2b$$
- $$a-b$$
Возьмем числа a и b в соответствии с условиями задания (a<0<b<1 ; |a|>|b|). Пусть $$a=-2 , b=0,5$$. Найдем значения представленных выражений:
- $$a+b=-2+0,5=-1,5$$
- $$-a=-(-2)=2$$
- $$2b=2*0,5=1$$
- $$a-b=-2-0,5=-2,5$$
Наибольшее число в данном случае равно 2, что соответсвтует 2 варианту ответа
Задание 1665
Сравните числа x и y, если $$x=(2,2*10^{-2})*(3*10^{-1})$$, $$y=0,007$$. В ответ запишите меньшее из чисел.
Найдем значение х, воспользуемся свойствами степеней: $$x=(2,2*10^{-2})*(3*10^{-1})=$$$$2,2*3*10^{-2+(-1)}=$$$$6,6*10^{-3}=0,0066$$. Так как 0,0066<0,007, то и x<y.
Задание 1666
О числах a, b, c и d известно, что $$a<b$$, $$b=c$$, $$d>c$$. Сравнитe числа d и a.
В ответе укажите номер правильного варианта.
- $$d=a$$
- $$d>a$$
- $$d<a$$
- Сравнить невозможно
Так как $$b=c$$ и $$a<b$$, то $$a<c$$. Так как $$d>c$$,то $$d>a$$. Правильным ответом является вариант под номером 2
Задание 1667
Известно, что $$0<a<1$$. Выберите наименьшее из чисел.
В ответе укажите номер правильного варианта.
- $$a^2$$
- $$a^3$$
- $$-a$$
- $$\frac{1}{a}$$
Подберем значение а в соответствии с первоначальным условием $$0<a<1$$, пусть $$a=0,5$$. Найдем значение представленных вариантов:
- $$a^2=0,5^{2}=0,25$$
- $$a^3=0,5^{3}=0,125$$
- $$-a=-0,5$$
- $$\frac{1}{a}=\frac{1}{0,5}=2$$
Как видим, наименьшее из полученных чисел равно -0,5, следовательно, в ответе укажем 3 вариант ответа.
Задание 1668
Известно, что $$a<b<0$$. Выберите наименьшее из чисел.
В ответе укажите номер правильного варианта.
- $$a-1$$
- $$b-1$$
- $$ab$$
- $$-b$$
Возьмем любые значение а и b в соответствии с первоначальным условием: $$a<b<0$$. Пусть $$a=-2, b=-1$$. Найдем значения представленных вариантов:
- $$a-1=-2-1=-3$$
- $$b-1=-1-1=-2$$
- $$ab=(-2)*(-1)=2$$
- $$-b=-(-1)=1$$
Как видим, наименьшее из полученных значений равно -3, что соответствует 1 варианту ответа
Задание 1669
Числа a и b отмечены точками на координатной прямой. Расположите в порядке возрастания числа $$\frac{1}{a}$$, $$\frac{1}{b}$$ и 1.
В ответе укажите номер правильного варианта.
- $$\frac{1}{a}$$;1; $$\frac{1}{b}$$
- $$\frac{1}{b}$$; 1; $$\frac{1}{a}$$
- $$\frac{1}{a}$$; $$\frac{1}{b}$$; 1
- 1; $$\frac{1}{b}$$; $$\frac{1}{a}$$
Выберем значения a и b в соответствии с условиями задачи $$a<0<b<1, |a|<|b|$$. Пусть $$a=-0,5 , b=0,8$$. Тогда $$\frac{1}{a}=\frac{1}{-0,5}=-2$$, $$\frac{1}{b}=\frac{1}{0,8}=1,25$$.
Если расположить в порядке возрастания полученные числа и единицу, то получим $$-2, 1, 1,25$$ или $$\frac{1}{a}$$;1; $$\frac{1}{b}$$, что соответствует первому варианту ответа
Задание 1670
Какому из данных промежутков принадлежит число $$\frac{5}{9}$$?
В ответе укажите номер правильного варианта.
- $$[0,5; 0,6]$$
- $$[0,6; 0,7]$$
- $$[0,7; 0,8]$$
- $$[0,8; 0,9]$$
Найдем приблизительное значение данного числа (деление столбиком) и получим $$\frac{5}{9}\approx 0,555...$$. Округлим данное число до сотых $$0,(5)\approx 0,56$$. Данное число располагается между 0,5 и 0,6, что соответствует 1 варианту ответа
Задание 1671
На координатной прямой отмечено число а. Расположите в порядке убывания числа a, $$a^2$$ и $$\frac{1}{a}$$.
В ответе укажите номер правильного варианта.
- $$a^2$$; a; $$\frac{1}{a}$$
- $$a^2$$; $$\frac{1}{a}$$; a
- a; $$a^2$$; $$\frac{1}{a}$$
- a; $$\frac{1}{a}$$; $$a^2$$
Выберем значение а в соответствии с условием задания $$a<-1$$. Пусть $$a=-1,5$$. Тогда $$a^2=(-1,5)^{2}=2,25$$ и $$\frac{1}{a}=\frac{1}{-1,5}=-\frac{2}{3}$$.
Расположим в порядке убывания полученные числа: $$ 2,25;-\frac{2}{3} ; -1,5$$ или $$a^2$$; $$\frac{1}{a}$$; a, что соответствует 2 варианту ответа.