ОГЭ
Задание 3189
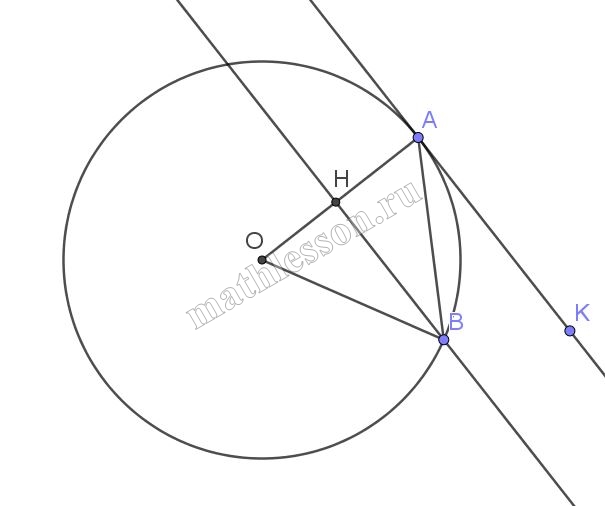
Из одной точки проведены к окружности две касательные, длина каждой из которых равна 12 см, а расстояние между точками касания равно 14,4 см. Найдите радиус окружности.
1) $$OB\perp AB$$ и $$OC\perp CA$$ (свойство радиусов в точку касания), ОА - общая, $$AC=AB$$ по условию $$\Rightarrow$$ $$\bigtriangleup OBA=\bigtriangleup OAC$$
2) $$\bigtriangleup ABH=\bigtriangleup AHC$$ (АH - общая; $$\angle BAH=\angle HAC$$; $$AB=AC$$) $$\Rightarrow$$ $$BH=HC$$ и $$BC\perp OA$$ $$\Rightarrow$$ $$BH=HC=0,5BC=14,4\cdot0,5=7,2$$
3) По теореме Пифагора $$AH=\sqrt{AB^{2}-BH^{2}}=\sqrt{12^{2}-7,2^{2}}=\sqrt{92,16}=9,6$$
4) из $$\bigtriangleup BHA\sim \bigtriangleup BOA$$: $$\frac{HA}{AB}=\frac{BH}{OB}$$ $$\Rightarrow$$ $$OB=\frac{AB\cdot BH}{HA}=\frac{12\cdot7,2}{9,6}=9$$
Задание 4991
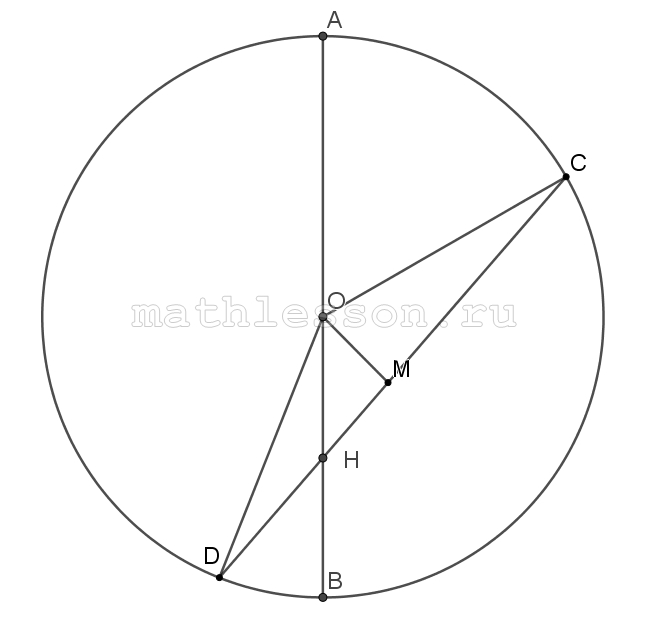
Через концы хорды, длина которой 30, проведены две касательные, до пересечения в точке А. Найдите расстояние от точки А до хорды, если радиус окружности равен 17.
1) Треугольник OCD - равнобедренный (OC=OD - Радиусы). Треугольник OCA равен треугольнику OAD (оба прямоугольные по свойству касательной и радуиса в точку касания, AC=AD по свойству касательной, OA - общая). Тогда углы COA и DOA равны, тогда треугольники COH и OHD равны. Тогда $$CH=\frac{1}{2}CB=15$$; $$OH=\sqrt{OC^{2}-CH^{2}}=\sqrt{17^{2}-15^{2}}=8$$;
2) Пусть $$CA=x$$,$$HA=y$$, тогда по теореме Пифагора и по формуле высоты прямоугольного треугольника как произведение катетов деленное на гипотенузу:
$$\left\{\begin{matrix}CA^{2}+CO^{2}=OA^{2}\\CH=\frac{OC\cdot CA}{OA}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x^{2}+17^{2}=(8+y)^{2}\\15=\frac{17\cdot x}{8+y}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$120+15y=17\cdot x$$; $$y=\frac{17x-120}{15}$$; $$x^{2}+289=(8+\frac{17x-120}{15})^{2}$$; $$x^{2}+289=\frac{289x^{2}}{225}$$; $$225x^{2}+289\cdot225=289x^{2}$$ $$\Leftrightarrow$$ $$64x^{2}=289\cdot225$$;$$x=\frac{17\cdot15}{8}=31,875$$; $$y=28,125=28\frac{1}{8}$$
Задание 5367
В окружности радиуса 16 см проведена хорда длиной, равной 8 см. через один конец хорды проведена касательная, а через другой – секущая, параллельная касательной. Найдите расстояние между касательной и секущей.
Задание 5513
Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD, если АВ = 24, а расстояние от центра окружности до хорд АВ и CD равны соответственно 16 и 12.
1) Пусть О - центр окружности, $$OH\perp AB$$ и $$OM\perp CD$$;
2) $$OB=OA$$ - радиусы, $$OH$$ - общий катет $$\Rightarrow$$ $$\bigtriangleup OHB=\bigtriangleup OHA$$ $$\Rightarrow$$ $$AH=HB=\frac{1}{2}AB=12$$;
3) $$OB=\sqrt{OH^{2}+HB^{2}}=20$$ (по т. Пифагора); $$OD=OB$$ - радиусы.
4) $$DM=\sqrt{OD^{2}-OM^{20}}=16$$ (по т. Пифагора);
5) $$DM=MC$$ (аналогично п. 2) $$\Rightarrow$$ $$CD=32$$
Задание 5514
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 18, а сторона AC в 1,2 раза больше стороны BC.
1) Пусть $$BC=x$$ $$\Rightarrow$$ $$AC=1,2x$$;
2) $$BKPC$$ - вписан $$\Rightarrow$$ $$\angle KPC+ \angle KBC=180^{\circ}$$ $$\Rightarrow$$ $$\angle APK=\angle ABC$$. Аналогично $$\angle AKP=\angle PCB$$ $$\Rightarrow$$ $$\bigtriangleup APK\sim \bigtriangleup ABC$$;
3) из п. 2: $$\frac{AK}{AC}=\frac{KP}{BC}$$ $$\Rightarrow$$ $$KP=\frac{AK\cdot BC}{AC}=\frac{18\cdot x}{1.2x}=15$$
Задание 5515
Окружность, вписанная в треугольник ABC , касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 49°, 69° и 62°.
1) $$\angle PKM$$ - вписанный и опирается на $$\smile PM$$. Но и $$\angle PMB$$ опирается на эту же хорду (угол между хордой и касательной равен половине дуги, на которую опирается) $$\Rightarrow$$ $$\angle PMB=\angle PKM=62^{\circ}$$ аналогично $$\angle MPB=62^{\circ}$$, тогда $$\angle B=180^{\circ}-2\cdot 62^{\circ}=56^{\circ}$$
2) Аналогично п.1 : $$\angle A=180^{\circ}-2\cdot 49^{\circ}=82^{\circ}$$; $$\angle C=180^{\circ}-2\cdot 69^{\circ}=42^{\circ}$$
Задание 5516
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 15, AC = 25.
1) Пусть О - центр окружности. М - точка пересечения $$AC$$ и окружности.
2) По свойству касательной и секущей: $$AM\cdot AC=AB^{2}$$
Пусть $$M=x$$, тогда $$AM=25-x$$.
Получим: $$(25-x)\cdot25=15^{2}$$ $$\div25$$ $$\Rightarrow$$
$$25-x=9$$ $$\Rightarrow$$ $$x=16=CM$$ - диаметр
Задание 5517
В треугольнике ABC угол B равен 72°, угол C равен 63°, $$BC=2\sqrt{2}$$. Найдите радиус описанной около этого треугольника окружности.
1) $$\angle A=180^{\circ}-(\angle B-\angle C)=45^{\circ}$$
2) Пусть $$R$$ - радиус описанной окружности, тогда : $$\frac{BC}{\sin A}=2R$$ $$\Rightarrow$$ $$R=\frac{BC}{\sin A}=\frac{2\sqrt{2}}{2\cdot\frac{\sqrt{2}}{2}}=2$$
Задание 6788
Хорда круга пересекает диаметр под углом 30 и делит его на части длиной 11 см и 55 см. Найдите расстояние от центра круга до хорды.
1) $$AB=AH+HB=66$$$$\Rightarrow$$ $$OA=OB=33$$(радиусы)
2) $$OH=OB-HB=33-11=22$$
3) из $$\Delta OHM$$: $$OM=OH*\sin OHM$$; $$OM=22*\frac{1}{2}=11$$