ОГЭ
Задание 1953
Сторона равностороннего треугольника равна 10. Найдите его площадь, делённую на $$\sqrt{3}$$.
Из формулы площади треугольника: $$S=\frac{1}{2}*10*10*\sin 60^{\circ}=25\sqrt{3}$$, в ответе необходимо указать значение без $$\sqrt{3}$$, то есть 25
Задание 1954
Периметр равностороннего треугольника равен 30. Найдите его площадь, делённую на $$\sqrt{3}$$.
- Пусть a - сторона равностороннего треугольника, тогда $$a=\frac{P}{3}=10$$
- Из формулы площади треугольника: $$S=\frac{1}{2}*10*10*\sin 60^{\circ}=25\sqrt{3}$$, в ответе необходимо указать значение без $$\sqrt{3}$$, то есть 25
Задание 1955
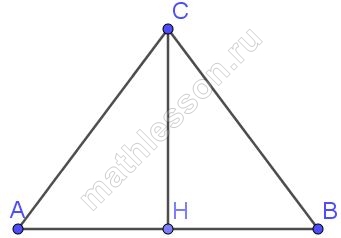
Высота равностороннего треугольника равна 10. Найдите его площадь, делённую на $$\frac{\sqrt{3}}{3}$$.
- Из треугольника ACH: $$AC=\frac{CH}{\sin A}=\frac{10}{\frac{\sqrt{3}}{2}}=\frac{20}{\sqrt{3}}$$
- Так как треугольник равносторонний, то AC=AB, тогда из формулы площади треугольника: $$S=\frac{1}{2}CH*AB=\frac{100}{\sqrt{3}}$$. В ответе необходимо указать результат, деленный на $$\frac{\sqrt{3}}{3}$$: $$\frac{100}{\sqrt{3}}:\frac{\sqrt{3}}{3}=100$$
Задание 1956
В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на $$\sqrt{3}$$
По формуле площади треугольника $$S=\frac{10*10*\sin 120^{\circ}}{2}=\frac{1}{2}*10*10*\frac{\sqrt{3}}{2}=25\sqrt{3}$$. В ответе необходимо указать ответ, деленный на $$\sqrt{3}$$, то есть 25
Задание 1957
В равнобедренном треугольнике боковая сторона равна 10, основание — $$5(\sqrt{6}-\sqrt{2})$$, а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
По формуле площади треугольника $$S=\frac{AB*AC*\sin B}{2}=\frac{1}{2}*10*10*\frac{1}{2}=25$$
Задание 1958
В равнобедренном треугольнике ABC AC=BC. Найдите AC, если высота CH=12, AB=10.
- По свойству высоты равнобедренного треугольника, проведенной к основанию: $$AH=HB=\frac{1}{2}AB=5$$
- По теореме Пифагора из треугольника ACH: $$AC=\sqrt{12^{2}+5^{2}}=13$$
Задание 1959
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
- Найдем полупериметр данного треугольника: $$p=\frac{34*2+60}{2}=64$$
- По формуле Герона: $$S=\sqrt{64(64-34)^{2}(64-60)}=480$$
Задание 1960
Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
- Найдем основание равнобедренного треугольника : $$216-2*78=60$$
- Полупериметр данного треугольника: $$p=\frac{216}{2}=108$$. По формуле Герона: $$S=\sqrt{108(108-78)^{2}(108-60)}=2160$$
Задание 2664
Боковая сторона равнобедренного треугольника равна 39, а основание равно 30. Найдите площадь этого треугольника.
|
1) BD - высота и медиана $$\Rightarrow$$ $$DC=15$$ 2) $$BD=\sqrt{BC^{2}-DC^{2}}=\sqrt{39^{2}-15^{2}}=36$$' 3) $$S=\frac{1}{2}AC\cdot BD=\frac{1}{2}\cdot 30\cdot 36=540$$ |
 |
Задание 2922
Боковая сторона равнобедренного треугольника равна 26, а основание равно 48. Найдите площадь этого треугольника.
|
AB=26 AC=48 Проведем высоту(медиана и биссектрисса) BH. AH будет равна половине AC = 24 По теореме Пифагора из треугольника AHB: $$BH=\sqrt{AB^{2}-AH^{2}}=10$$ Тогда площадь будет равна 0.5*10*48=240 |
Задание 4937
Угол при вершине, противолежащей основанию равнобедренного треугольника равен $$150^{\circ}$$. Боковая сторона треугольника равна 8. Найдите площадь этого треугольника.
$$S=\frac{1}{2}\cdot8\cdot8\cdot\sin150^{\circ}=\frac{1}{2}\cdot8\cdot8\cdot\frac{1}{2}=16$$
Задание 5081
Боковая сторона равнобедренного треугольника равна 13, а основание равно 24. Найдите площадь этого треугольника.
$$h=\sqrt{13^{2}-12^{2}}=5$$; $$S=\frac{1}{2}\cdot a\cdot h=\frac{1}{2}\cdot24\cdot5=60$$
Задание 5314
Боковая сторона равнобедренного треугольника равна 26, а основание равно 10. Найдите площадь этого треугольника.
Высота треугольника : $$h = \sqrt{26^{2}-5^{2}}=\sqrt{651}$$. Тогда его площадь $$S=\frac{1}{2}h*10=5\sqrt{651}$$
Задание 6112
Боковая сторона равнобедренного треугольника равна 26, а основание равно 12. Найдите площадь этого треугольника
Воспользуемся формулой Герона для вычисления площади треугольника. Найдем полупериметр: $$p=\frac{26+26+12}{2}=32$$. Тогда площадь треугольника равна: $$S=\sqrt{32(32-62)(32-26)(32-12)}=48\sqrt{10}$$