ОГЭ
Задание 2669
Известно, что графики функций y=x2+p и y=2x-5 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
$$y=x^{2}+p$$
$$y=2x-5$$
| $$x^{2}+p=2x-5$$ | имеет одно решение, т.к. D=0 |
$$x^{2}-2x+5+p=0$$
$$D=4-4(5+p)=0$$
$$\Rightarrow p=-4\Rightarrow x=1 y=-3$$
Задание 2927
Постройте график функции $$y=\frac{(x-9)(x^{2}-9)}{x^{2}-6x-27}$$ и определите, при каких значениях k построенный график не будет иметь общих точек с прямой у=kх.
Решение временно отсутствует, можете найти его в моем видео-разборе ( вначале варианта )
Задание 3141
Найдите все значения k, при каждом из которых прямая y= kx - 1 имеет с графиком функции y=x2-4x+3 ровно одну общую точку. Постройте этот график и все такие прямые.
Текстовое решение временно недоступно, вы можете найти его в видео в начале варианта
Задание 3273
Найдите все значения а, при каждом из которых уравнение $$|3x+2|+|3x-2|=ax+4$$ имеет ровно два решения.
Пусть $$f(x)=|3x+2|+|3x-2|$$
$$g(x)=ax+4$$
|
$$3x+2$$ $$3x-2$$ |
$$x<-\frac{2}{3}$$ $$\Rightarrow$$ $$f(x)=-3x-2-3x+2=-6x$$
$$x\in [-\frac{2}{3};\frac{2}{3}]\Rightarrow f(x)=3x+2-3x+2=4$$
$$x\geq \frac{2}{3}\Rightarrow f(x)=3x+2+3x-2=6x$$
$$g(x)=ax+4$$ при $$a\in(-6;0)\cup(0;6)$$
Задание 4869
Постройте график функции $$y=\frac{(\sqrt{x^{2}-5x+6})^{2}}{x-3}$$ и найдите все значения а при которых прямая $$y=a$$ не имеет с графиком ни одной общей
Задание 5086
Постройте график функции $$y=\frac{(x^{2}-4)(x-4)}{x^{2}-2x-8}$$ и определите, при каких значениях $$k$$ построенный график не будет иметь общих точек с прямой $$y=kx$$
Задание 5319
Постройте график функции $$y=\frac{(x-4)(x^{2}-4)}{x^{2}-6x+8}$$ и определите, при каких значениях k построенный график не будет иметь общих точек с прямой у=kx
Найдем область определения заданной функции: $$x^{2}-6x+8 \neq 0 \Leftrightarrow $$$$x_{1} \neq 2 ; 4$$
Преобразуем данную функцию с учетом полученной области определения: $$\frac{(x-4)(x^{2}-4)}{x^{2}-6x+8}=$$$$\frac{(x-4)(x-2)(x+2)}{(x-4)(x-2)}=x+2$$. То есть график функции $$y=x+2$$ совпадает с графиком начальной функции при наличии области ее определения.
Получаем, что точки (2;4) и (4;6) пустые, следовательно, чтобы прямая y=kx не имела с графиком пересечений, она должна пройти через эти точки. Подставим их координаты в уравнение прямой, чтобы найти k:
$$4=2k \Leftrightarrow$$$$k=2$$
$$6=4k \Leftrightarrow$$$$k=1,5$$
Так же прямая не будет иметь пересечений, если она будет параллельна графику начальной функции. Две прямые $$y_{1}=k_{1}x+b_{1}$$ и $$y_{2}=k_{2}x+b_{2}$$ параллельны в том случае, если коэффициенты при х у них одинаковы ($$k_{1}=k_{2}$$, а свободные - разные ($$b_{1} \neq b_{2}$$). То есть k=1 тоже будет ответом.
Задание 6259
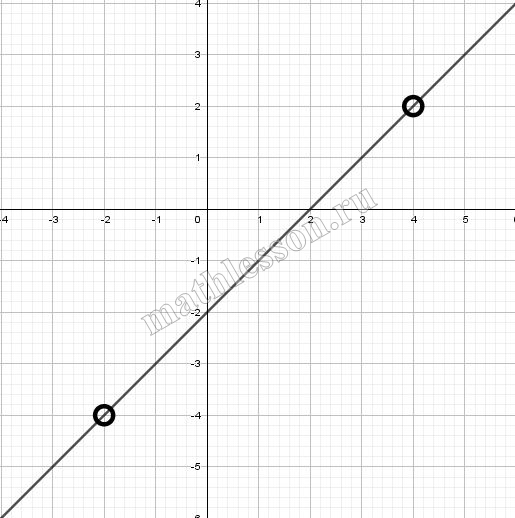
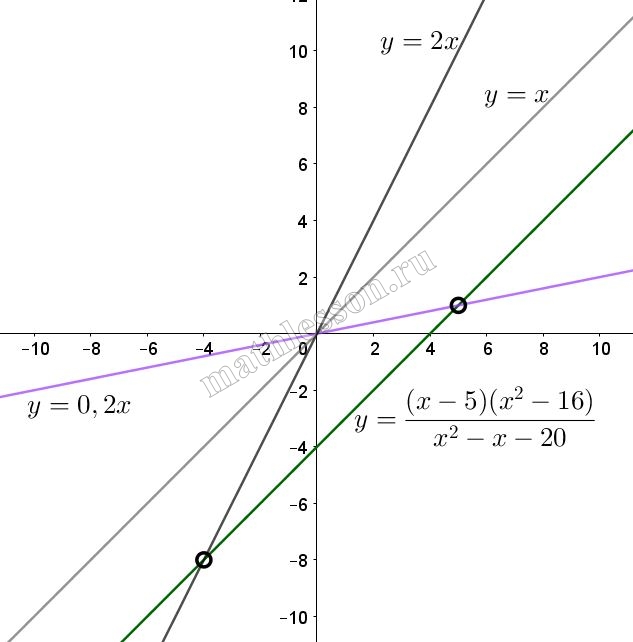
Постройте график функции $$y=\frac{(x-5)(x^{2}-16)}{x^{2}-x-20}$$ и определите, при каких значениях k построенный график не будет иметь общих точек с прямой $$y=kx$$ .
$$y=\frac{(x-5)(x^{2}-16)}{x^{2}-x-20}$$
Найдем область определения. Так как есть знаменатель, то он не равен нулю:
$$x^{2}-x-20\neq 0$$
$$\left\{\begin{matrix}x_{1}+x_{2}\neq 1 \\x_{1}*x_{2}\neq -20 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}\neq -4 \\x_{2}=5 \end{matrix}\right.$$
Воспользуемся формулой: $$ax^{2}+bx+c=a(x-x_{1})(x-x_{2})$$:
$$y=\frac{(x-5)(x-4)(x+4)}{(x+4)(x-5)}=x-4$$
Не будет иметь если $$y=kx$$ пройдет через точку (5;1) или (-4;-8), а так же если будет параллельна:
1)$$1=5*k\Rightarrow k=0,2$$
2) $$-8=(-4)k\Rightarrow k=2$$
3) Прямые параллельны, если их коэффициенты при х равны. То есть прямая $$y=kx$$ параллельна $$y=x-4$$ при $$k=1$$
Задание 6551
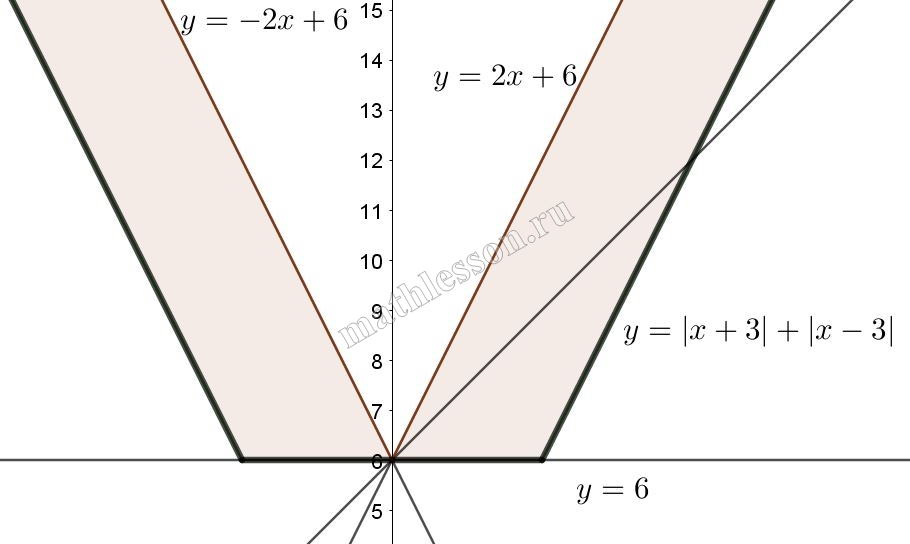
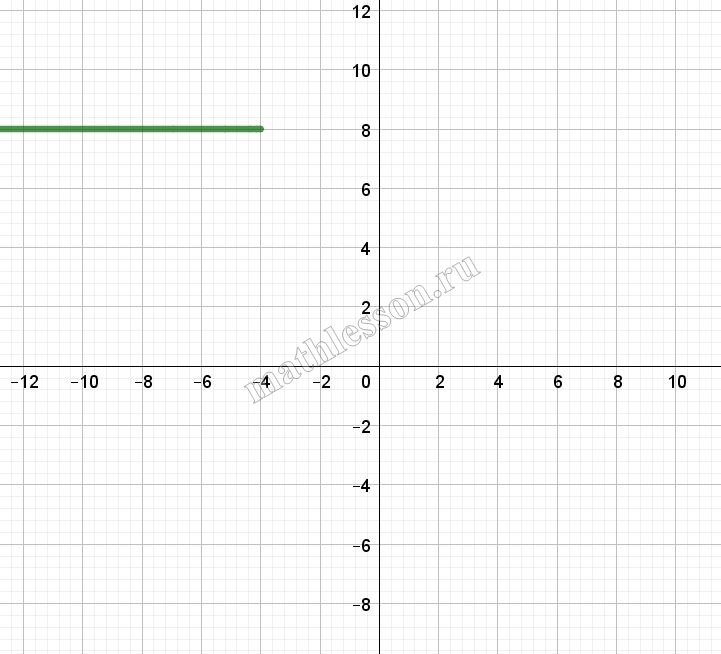
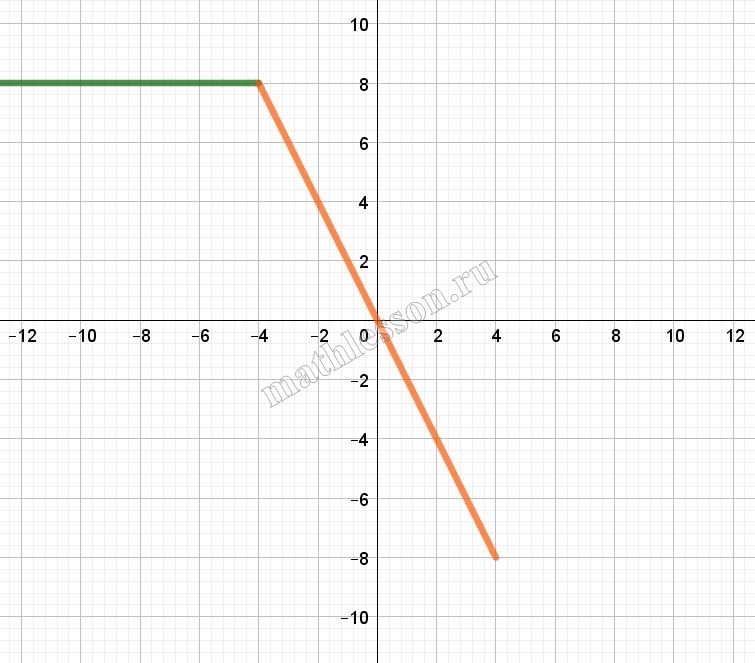
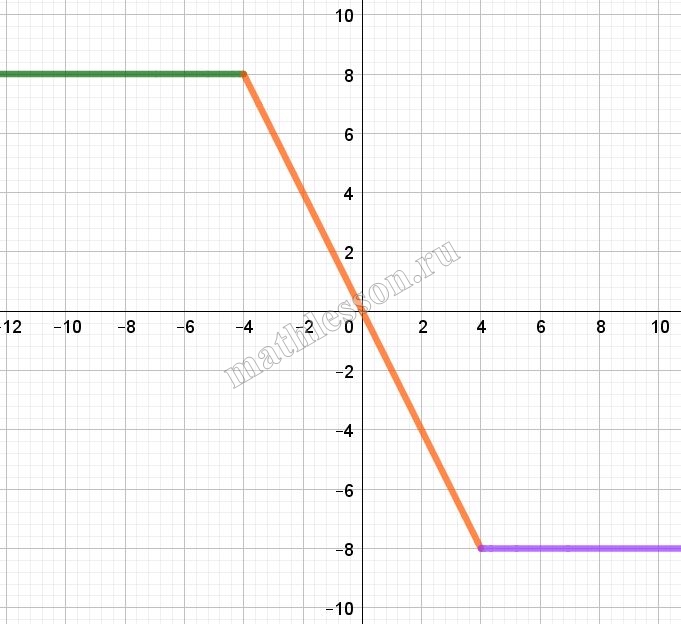
Постройте график функции $$y=|x+3|+|x-3|$$ и найдите все значения а, при которых прямая $$y=ax+6$$ имеет с графиком ровно две общие точки.
Раскроем модуль:
$$x\leq -3\Leftrightarrow y=-x-3-x+3=-2x$$
$$x \in (-3, 3]\Leftrightarrow y=x+3-x+3=6$$
$$x>3\Rightarrow y=x+3+x-3=2x$$
Начертим график:
Видим, что две точки пересечения будут в том случае, если прямая лежит в первой четверти при $$a\in(0;2)$$ (от момента, когда она будет параллельна оси Ох, до момента, когда она будет параллельна прямой $$y=2x$$) и, если прямая лежит во второй четверти при $$a\in(-2;0)$$ (от момента, когда она будет параллельна $$y=-2x$$, до момента, когда она будет параллельна оси Ох): $$a \in (-2;0)\cup (0;2)$$
Задание 6598
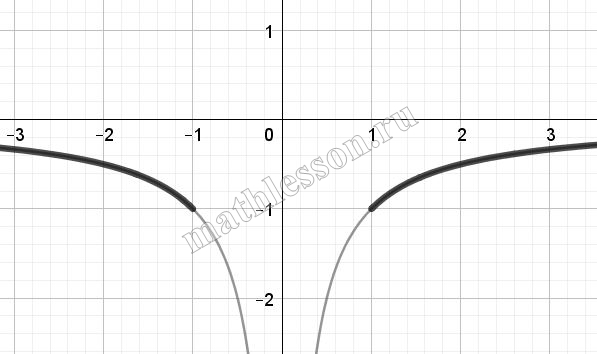
Постройте график функции $$y=\left\{\begin{matrix}-x^{2}, |x|\leq 1\\-\frac{1}{\left | x \right |}, |x|>1\end{matrix}\right.$$ и определите, при каких значениях c прямая y=c будет иметь с графиком ровно две общие точки
Рассмотрим график функции $$y=-x^{2}$$ с учетом того, что $$-1 \leq x \leq 1$$: это парабола, ветви вниз, вершина в начале координат (черным отмечена часть графика, с учетом ограничений)

Рассмотрим график функции $$y=-\frac{1}{\left | x \right |}$$ с учетом, что $$x \in (-\infty; 1)\cup (1;+\infty)$$: без модуля была бы гипербола, располагающаяся во второй и четвертой координатной четвертях, с учетом модуля левая ее ветвь отобразится относительно оХ (черным выделена часть, с учетом ограничений по х):
Объеденим графики:
Как видим, две точки пересечения прямая будет иметь в том случае, когда c=1
Задание 6713
Постройте график функции $$y=|x-4|+|x+4|$$ и найдите все значения k , при которых прямая $$y=kx$$ имеет с графиком данной функции ровно одну общую точку.
Рассмотрим раскрытие модулей:
$$\left\{\begin{matrix}x\leq -4, y=-x+4-(-x-4)=8\\x \in (-4,4)(1), y =-x+4-(x+4)=-2x-8\\x\geq 4(2), y=x-4-(x+4)=-8(3)\end{matrix}\right.$$
Построим график данной кусочной функции:
Как видим, одна точка пересечения у графика будет в случае: $$k \in (-\infty ;-2)\cup [0;+\infty )$$

Задание 7088
Постройте график функции $$\left\{\begin{matrix}-x^{2}, |x|\leq 2\\ \frac{8}{x},|x|>1\end{matrix}\right.$$ и определите, при каких значениях а прямая y=а будет иметь с графиком ровно одну общую точку
Построим график функции $$y=-x^{2}$$ и оставим часть при $$\left | x \right |\leq 2(x \in [-2 ;2])$$.
Построим $$y=\frac{8}{x}$$ при $$x \in (-\infty ;-2)\cup (2; +\infty )$$
1 общая точка при $$a \in [0 ; 4)$$
Задание 7278
Постройте график функции $$y=|2|x|-6|$$ и найдите все значения а при которых прямая $$y=a$$ имеет с графиком ровно три общие точки.
Раскроем внутренний модель : $$\left\{\begin{matrix}y=\left | 2x-6 \right |,x>0(1)\\y=\left | -2x-6 \right |, x<0 (2)\end{matrix}\right.$$
1) Если $$2x-6\geq 0$$ (или $$x\geq 3$$), то $$y=2x-6$$ ,если $$x<3$$, то $$y=-2x+6$$
2) Если $$-2x-6\geq 0\Leftrightarrow$$ $$x\leq -3$$, то $$y=-2x-6$$, если $$x\geq -3$$, то $$y=2x+6$$
Тогда получим следующую совокупность :
$$\left[\begin{matrix}\left[\begin{matrix}\left\{\begin{matrix}x\geq 3 & & \\y=2x-6 & &\end{matrix}\right. & & \\\left\{\begin{matrix}0\leq x<3 & & \\y=-2x+6& &\end{matrix}\right.& &\end{matrix}\right. & & \\\left[\begin{matrix}\left\{\begin{matrix}x\leq -3 & & \\y=-2x-6& &\end{matrix}\right. & & \\\left\{\begin{matrix}-3<x<0 & & \\y=2x+6& &\end{matrix}\right. & &\end{matrix}\right.& &\end{matrix}\right.$$
Прямая y=a имеет с графиком 3 общие точки при a=6