ОГЭ
Задание 2814
Найдите все значения k при которых прямая $$y=kx$$ пересекает в двух точках ломаную, заданную условиями: $$y=\left\{\begin{matrix}x-2, x<6\\10-x, x\geq6\end{matrix}\right.$$
$$y=kx$$ проходит через центр системы координат
1) $$k\geq0$$ и до момента, пока пройдет через $$(6; 4)$$
$$4=k\cdot 6\Rightarrow k=\frac{4}{6}=\frac{2}{3}$$ $$\Rightarrow k\in \left [ 0; \frac{2}{3} \right)$$
2) $$k<0$$ до момента, пока не станет параллельна $$y=10-x$$, то есть $$k>-1$$ $$\Rightarrow$$ $$k\in(-1; 0)$$
Задание 4943
Постройте график функции $$y=\left\{\begin{matrix}|x|,-1\leq x\leq2\\-x^{2}+6x-6,x>2;x<-1\end{matrix}\right.$$
определите, при каких значениях $$a$$ прямая $$y=a$$ имеет с графиком ровно две общие точки.
Построим обы графика функция на одной системе координат
Отметим части графика с учетом ограничений по х (выделены черным цветом)
Сотрем ненужные части (важно помнить, что закращенный концы будут у графика модуля, так как именно там нестрогие неравенства)
Прямая $$y=a$$, это прямая, параллельная оси Ox. Как видим по графику две точки пересечения получатся в случае если $$a\in(-\infty;-13)\cup[0]\cup(1;3)$$
Задание 5039
Постройте график функции
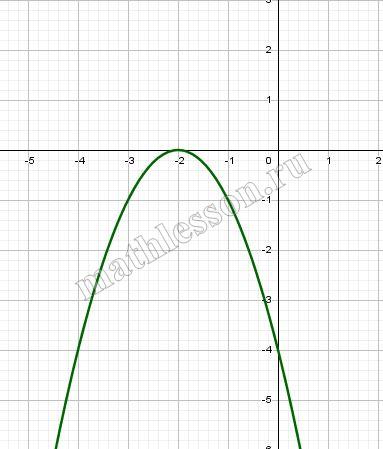
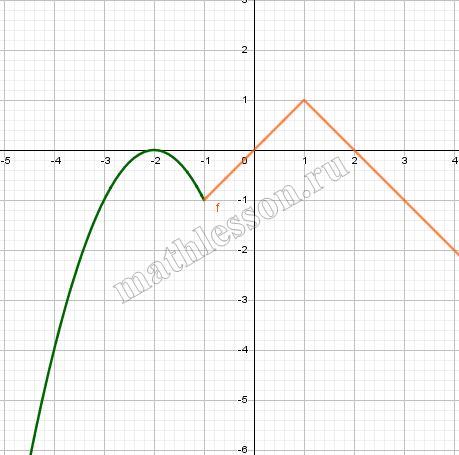
$$y=\left\{\begin{matrix}-x^{2}-4x-4,x<-1\\1-|x-1|,x\geq-1\end{matrix}\right.$$
и определите, при каких значениях $$m$$ прямая $$y=m$$ имеет с графиком ровно две общие точки.
Задание 5414
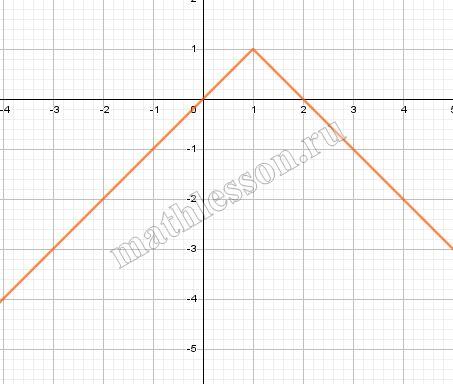
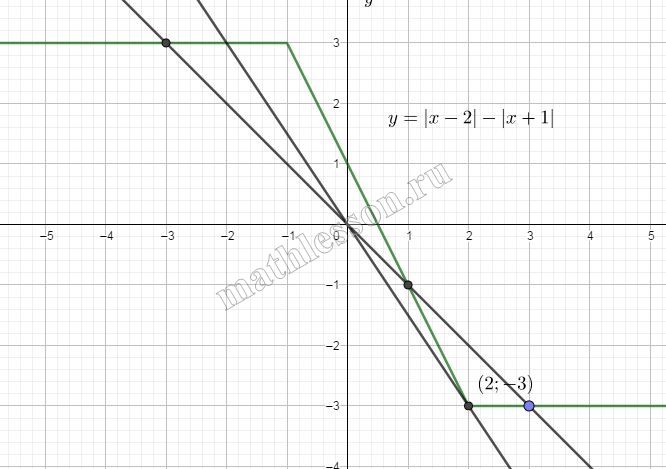
Постройте график функции $$y=|x-2|-|x+1|$$ и определите, при каких значениях k прямая y=kx имеет с графиком ровно три общие точки.
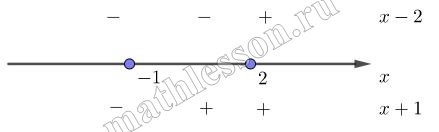
$$y=\left | x -2 \right |-\left | x +1 \right |$$. Уберем модули. $$x -2=0$$ при $$x=2$$, а $$x+1=0$$, при х=-1$$. Отметим полученные точки на координатной прямой и посмотрим, какие значения принимают подмодульные выражения на различных промежутках:
Получили три интервала:
1)$$\left\{\begin{matrix}x \leq -1\\y=-x +2+x +1=3 \end{matrix}\right.$$
2)$$\left\{\begin{matrix} -1<x<2\\y=-x +2-x -1=-2*x +1\end{matrix}\right.$$
3)$$\left\{\begin{matrix}x \geq 2 \\y=x -2-x -1=-3 \end{matrix}\right.$$
Построим график с учетом полученных интервалов и их кусочных функций:
Графиком функции $$y=kx$$ является прямая, проходящая через начало координат. Очевидно, что для 2х пересечений прямая должна пройти через координату (2;-3).
Найдем коэффициент k:
$$-3=k*2\Leftrightarrow$$$$k=-1,5$$
Тогда, для 3х пересечений, коэффициент должен быть больше, чем -1,5, но меньше 0, то есть $$k \in(-1,5;0)$$
Задание 6165
Найдите все значения k при которых прямая у = kx пересекает в двух точках ломаную, заданную условиями:$$\left\{\begin{matrix}x-3,x<5\\ 7-x,x\geq 5\end{matrix}\right.$$
$$y=\left\{\begin{matrix}x-3, x<5 & & \\7-x, x\geq 5& &\end{matrix}\right.$$
Начертим график данной функции :
При a>0 до момента , когда пройдет поезд (5;2) (прямая розового цвета) : $$2=5*k\Rightarrow k=0,4$$, то есть $$k\in [0; 0,4)$$.
При a<0, пока не станет параллельна (прямая серого цвета) прямой y=7-x, то есть $$a\in (-1; 0)$$ Итог (-1; 0,4)
Задание 6212
Постройте график функции $$y=\left\{\begin{matrix}-x^{2},|x|\leq 2\\ \frac{8}{x},|x|>2\end{matrix}\right.$$
и определите, при каких значениях а прямая y=аx будет иметь с графиком единственную общую точку
Начертим график данной функции $$y=\left\{\begin{matrix} -x^{2}, \left | x \right |\leq 2\\ \frac{8}{x}, \left | x \right |>0\end{matrix}\right.$$
Учтем, что график $$y=-x^{2}$$ при $$x\in [-2;2]$$ (на концах закрашенные точки, так как неравенство нестрогое), на остальной части область определения $$y=\frac{8}{x}$$.
$$y=a$$ - прямая, параллельная оси Ox, тогда одну точку будет иметь при $$a\in [0;4)$$
Задание 6646
Постройте график функции $$y=\left\{\begin{matrix}x^{2}+4x,x<1\\ \frac{5}{x},x\geq 1\end{matrix}\right.$$ и определите, при каких значениях а прямая y=а будет пересекать построенный график в трех точках.
Рассмотрим $$y=x^{2}+4x$$. Найдем координаты вершины параболы: $$x_{0}=-\frac{4}{2}=-2$$; $$y_{0}=-4$$. Построим график функции с учетом ограничения по х (выделен черным)
Рассмотрим $$y=\frac{5}{x}$$ - это гипербола, расположенная в первой и третьей координатных четвертях. С учетом ограничениях по х (выделен черным):
Объединим полученные кусочные функции:
Прямая $$y=a$$ - прямая, параллелная оси Ох. Три точки пересечения будет при $$a \in (0;5)$$
Задание 6858
Постройте график функции $$y=\left\{\begin{matrix}-x^{2}-4x, x\geq 0\\-2x, x<0\end{matrix}\right.$$ и определите, при каких значениях m он имеет ровно две общие точки с прямой y=m.
Построим $$y=-x^{2}-4x$$. Вершина параболы: $$x_{0}=-\frac{-4}{-2}=-2$$, тогда $$y_{0}=-(-2)^{2}-4(-2)=4$$ (Черным выделена часть графика, с учетом $$x\geq 0$$):
Построим $$y=-2x$$ - это прямая, проходящая во второй и четвертой четвертях через начало координат (черным выделено с учетом условия $$x<0$$:
Объединим полученные кусочные функции:
С учетом того, что график функции $$y=m$$ - это прямая, параллельная оси Ох, то 2 точки пересечения с первоначальным графиком быть не может
