ОГЭ
Задание 1858
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.
$$\angle A=\angle BAC+\angle CAD=30+45=75^{\circ}$$, тогда по свойству углов трапеции: $$\angle B=180-\angle A=105^{\circ}$$
Задание 1860
Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
Так как дана равнобедренная трапеция, то сумма острых углов при большем основании будет составлять 140 градусов, $$\angle A=\angle B=\frac{140}{2}=70^{\circ}$$, по свойству углов трапеции: $$\angle D=180-\angle A=110^{\circ}$$
Задание 1861
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.
Пусть меньший угол равен х, тогда больший угол равен 2х. По свойству углов трапеции получаем, что $$x+2x=180\Leftrightarrow$$$$x=60$$, то есть меньший угол составляет $$60^{\circ}$$
Задание 1863
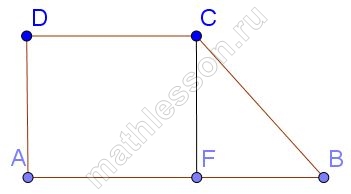
Тангенс острого угла прямоугольной трапеции равен $$\frac{5}{6}$$. Найдите её большее основание, если меньшее основание равно высоте и равно 15.
Опустим высоту CF, тогда из прямоугольного треугольника CFB: $$FB=\frac{CF}{tgB}=\frac{15}{\frac{5}{6}}=18$$. DC=AF=15, тогда AB=15+18=33.
Задание 1864
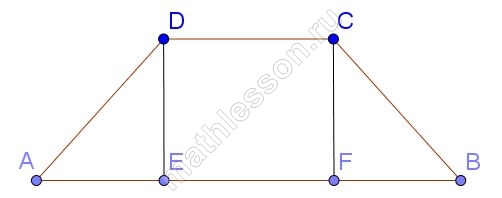
В равнобедренной трапеции известны высота 4, меньшее основание 8 и угол при основании $$45^{\circ}$$. Найдите большее основание.
Опустим высоты DE=CF=4, тогда из прямоугольного треугольника ADE: так как $$\angle A=45^{\circ}$$, то $$\angle ADE=90-45=45^{\circ}$$, следовательно, реугольник AED - равнобедренный, и AE=DE=4, аналогично FB=4. Но EF=DC=8, тогда AB=4+4+8=16.
Задание 1865
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
EG - средняя линия треугольника ADB, тогда $$EG=\frac{1}{2}=AB=5$$, аналогично GF - средняя линия треугольника DCB, тогда $$GF=\frac{1}{2}DC=2$$, наибольший в таком случае равен 5
Примечение: больший из отрезков всегда будет равен половине большего основания
Задание 1866
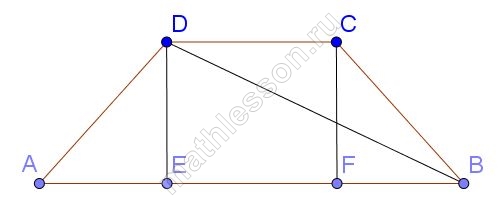
Основания равнобедренной трапеции равны 50 и 104, боковая сторона 45. Найдите длину диагонали трапеции.
Опустим две высоты DE=CF, тогда AE=FB (из равенства прямоугольных треугольников ADE и CFB по катету и гипотенузе), и DC=EF=50, тогда $$AE=FB=\frac{104-50}{2}=27$$. Тогда из прямоугольного треугольника ADE : $$DE=\sqrt{AD^{2}-AE^{2}}=\sqrt{45^{2}-27^{2}}=36$$, следовательно, EB=AB-AE=104-27=77. Тогда из прямоугольного треугольника DEB: $$DB=\sqrt{DE^{2}+EB^{2}}=\sqrt{77^{2}+36^{2}}=85$$
Задание 1867
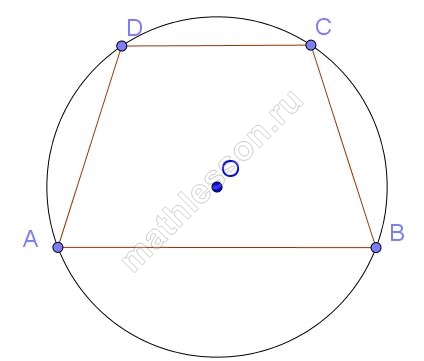
Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Запишите величины углов в ответ через точку с запятой в порядке неубывания.
По свойству вписанного четырехугольник $$\angle A+\angle C=180^{\circ}$$, пусть $$\angle A=49^{\circ}\Rightarrow$$$$\angle C=180-49=131^{\circ}$$. По свойству углов трапеции $$\angle B=180-\angle C=180-131=49^{\circ}$$, аналогично $$\angle D=180-\angle A=131^{\circ}$$
Задание 1868
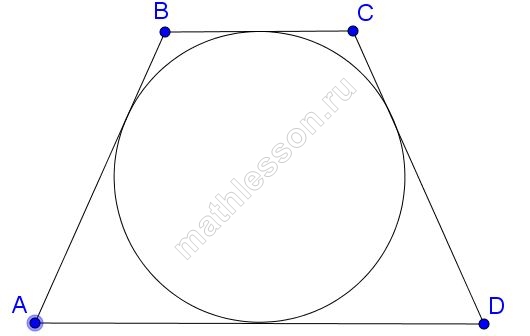
В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
По свойству описанного четырехугольника AD+BC=AB+CD, тогда сумма оснований тоже 24, средняя линия же равна полусумме оснований, то есть 24/2=12.
Задание 2850
В трапецию, сумма длин боковых сторон которой равна 26, вписана окружность. Найдите длину средней линии трапеции.
Условием того, что в четырехугольник( в том числе и в трапецию) можно вписать окружность является то, что сумма противоположных сторон у него одинакова. Значит, сумма боковых сторон, равна сумме оснований, то есть сумма оснований будет 26. Средняя линия равна полусумме оснований, то есть 26/2=13
Задание 2921
Основания трапеции равны 7 и 12. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
|
Из трекгольника ABC: MO=0.5BC=3.5 Из треугольника ACD: ON=0.5AD=6 |
 |
Задание 3011
| Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 3 и 9. Найдите длину основания BC. |
$$BC=9-3=6$$
Задание 3095
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.

$$D=180-C=180-120=60$$
Из CHB : $$CH=CD * \sin D = 25 \sin 60=25 * \frac{\sqrt{3}}{2}=\frac{25\sqrt{3}}{2}$$
$$AM=CH$$ ;
$$AB=\frac{AM}{\sin B}=\frac{\frac{25\sqrt{3}}{2}}{\frac{1}{2}}=25\sqrt{3}$$