ОГЭ
Задание 1909
Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.
1) $$OD=AB-BD=4$$
2) Треугольник OAD - прямоугольный, тогда по теореме Пифагора: $$AD=\sqrt{5^{2}-4^{2}}=3$$
3) OA=AC, OD - общая, тогда прямоугольные треугольники AOD и ODC равны, следовательно, AD=DC=3, и AC=6
Задание 1910

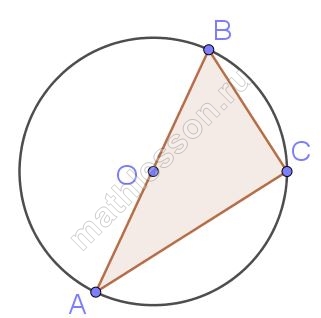
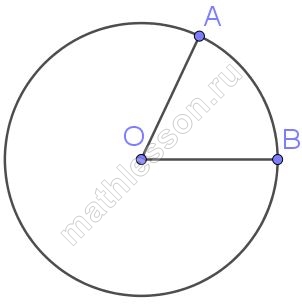
Найдите величину (в градусах) вписанного угла α, опирающегося на хорду AB, равную радиусу окружности.
1) Треугольник OAB - равносторонний, тогда $$\angle AOB = 60^{\circ}=\smile AB$$
2) $$\angle ADB=\angle \alpha=\frac{1}{2}\smile AB=30^{\circ}$$ (по свойству вписанного угла)
Задание 1911
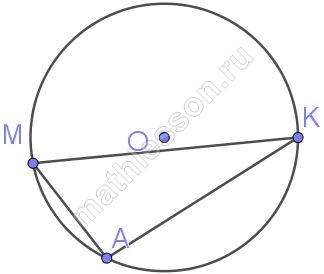
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
1) По свойству радиуса и касательной $$OB\perp AB$$, тогда треугольник OAB - прямоугольный
2) По теореме Пифагора $$OB=\sqrt{13^{2}-12^{2}}=5$$
Задание 1912
В треугольнике ABC угол C равен 90°, AC = 30 , $$BC=5\sqrt{13}$$. Найдите радиус окружности, описанной около этого треугольника.
1) По теореме Пифагора $$AB=\sqrt{30^{2}+(5\sqrt{13})^{2}}=35$$
2) По свойству прямоугольного треугольника, радиус описанной окружности равен половине гипотенузы, то есть $$R=\frac{35}{2}=17,5$$
Задание 1913
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
1)OA=OC (радиусы), AB - перпендикуляр (так как расстояние), тогда треугольники AOB и OBC прямоугольные и равные по катету и гипотенузе
2)AB=BC=0,5AC=36, тогда по теореме Пифагора из треугольника AOB: $$AO=\sqrt{36^{2}+27^{2}}=45$$, следовательно, диаметр составит $$2*45=90$$
Задание 1914
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Задание 1915
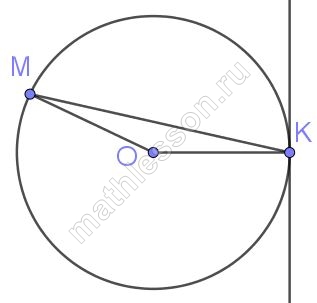
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
Треугольник OMK - равнобедренный (OM=OK - радиусы), тогда $$\angle OMK=\angle OKM$$
По свойству касательной и радиуса OK и касательная - перпендикулярны, тогда $$\angle OKM=90-83=7^{\circ}$$, тогда и угол OMK те же 7 градусов
Задание 1917
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 18, CD = 24, а расстояние от центра окружности до хорды AB равно 12.
Задание 1918
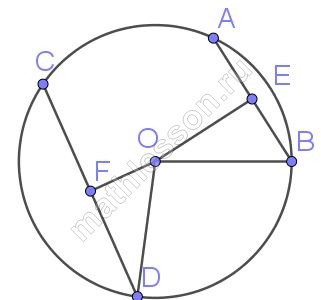
На окружности с центром O отмечены точки A и B так, что ∠AOB = 66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
Если острый угол AOB составляет 66 градуов, то развернутый составляет $$360-66=294^{\circ}$$
Пусть длина большей дуги равна х, тогда:
$$66^{\circ}- 99$$
$$294^{\circ}- x$$
$$x=\frac{294*99}{66}=441$$
Задание 2481
| Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k. |
| $$OA=OM=85$$ $$AB=80$$ $$\Rightarrow AL=BL=40$$ $$OL=\sqrt{OA^{2}-AC^{2}}=\sqrt{85^{2}-40^{2}}=75$$ $$ML=MO+OL=85+75=160$$ |
Задание 2662
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 18°. Найдите величину угла OMK. Ответ дайте в градусах.
|
1) ОМ - радиус $$\Rightarrow$$ МК - диаметр $$\Rightarrow$$ $$\smile LM=180^{\circ}$$ 2) $$\angle DKM=18^{\circ}$$ $$\Rightarrow$$ $$\smile KM=18\cdot 2=36^{\circ}$$ 3) $$\smile LK=\smile LM-\smile KM=180^{\circ}-36^{\circ}=144^{\circ}$$ 4) $$\angle OMK=\frac{\smile LM}{2}=72^{\circ}$$ |
 |
Задание 2886
Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
Введем следующие обозначения:

AH=HB=0.5AB=65 (так как AOB - равнобедренный и OH - высота)
$$OB=\sqrt{OH^2+HB^2}=97$$
OB - радиус, значит диаметр будет 97*2=194
Задание 3010
| Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 5. Найдите диаметр окружности. |
$$r=\sqrt{12^{2}+5^{2}}=13$$ $$d=2r=2\cdot13=26$$
Задание 3058
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Проведем радиусы в точки касания и получим два равных прямоугольных треугольника. Значит ОА - биссектриса угла А. Значит она делит угол пополам, и получаем в треугольнике угол в 30 градусов. А катет (в нашем случае это радиус окружности), лежащий напротив угла в 30 градусов, равен половине гипотенузы, то есть половине ОА или 3
Задание 3181
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 50. Найдите величину угла MOK. Ответ дайте в градусах.
Радиус, проведенный в точку касания, перпендикулярен касательной, значит ∠OKM = 90 - 50 = 40. Треугольник OMK равнобедренный ( так как OK ; OM - радиусы ). Значит ∠OMK = ∠OKM = 40 ∠MOK = 180 - ∠OMK - ∠OKM = 180 - 80 = 100