ОГЭ
Задание 2773
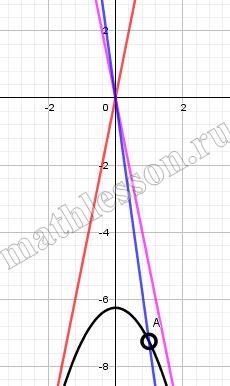
Постройте график функции $$y=x^{2}-4\left | x \right |-x$$ и определите, при каких значениях а прямая $$y=а$$ имеет с графиком ровно три общие точки.
| $$\left\{\begin{matrix}x\geq0\Rightarrow y=x^{2}-4x-x=x^{2}-5x\\x\leq0\Rightarrow y=x^{2}+4x-x=x^{2}+3x\end{matrix}\right.$$ |
1) $$y=x^{2}-5x$$ $$x_{0}=-\frac{-5}{2}=2,5$$ $$y_{0}=2,5^{2}-5\cdot2,5=-6,25$$
2) $$y=x^{2}+3x$$ $$x_{0}=-\frac{3}{2}=-1,5$$ $$y_{0}=(-1,5)^{2}+3\cdot(-1,5)=-2,25$$
Задание 2976
Постройте график функции $$y=|x^{2}-2x-3|$$ и определите, при каких значениях а прямая $$y=a$$ имеет с графиком три общие точки.
Текстовое решение временно отсутствует. Вы можете найти разбор в видео перед вариантом
Задание 3101
Постройте график функции $$y=5-\frac{x^{4}-x^{3}}{x^{2}-x}$$ и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
$$y=5-\frac{x^{4}-x^{3}}{x^{2}-x}$$ $$x^{2}-x\neq0$$ $$\Leftrightarrow$$ $$x\neq1$$; $$x\neq0$$ $$y=5-\frac{x^{2}(x^{2}-x)}{x^{2}-x}=5-x^{2}$$
Задание 3994
Постройте график функции $$y=5-\frac{x^{4}-x^{3}}{x^{2}-x}$$ и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
$$y=5-\frac{x^{4}-x^{3}}{x^{2}-x}$$
ОДЗ: $$x^{2}-x\neq0$$
$$\left\{\begin{matrix}x\neq0\\x\neq1\end{matrix}\right.$$
$$5-\frac{x^{4}-x^{3}}{x^{2}-x}=$$
$$=5-\frac{x^{2}(x^{2}-x)}{x^{2}-x}=5-x^{2}$$
$$y_{1}=5-x^{2}$$
То есть график первоначальной функции совпадает с графиком функции y1 при учете ОДЗ. Построим график y1 функции
Если прямая y=m проходит через оординаты 4 и 5, то получаем по одному пересечению, следовательно, их надо исключить, и тогда m будет принадлежать промежутку:
$$m\in(-\infty;4)\cup(4;5)$$
Задание 4058
Постройте график функции $$y=x^{2}-4|x|-x$$ и определите, при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
Если $$x\geq0\Rightarrow y=x^{2}-4x-x=x^{2}-5x$$
Если $$x<0\Rightarrow y=x^{2}+4x-x=x^{2}+3x$$
1) $$y=x^{2}-5x$$
$$x_{0}=-\frac{-5}{2}=2,5$$
$$y_{0}=2,5^{2}-5\cdot2,5=-6,25$$
2) $$y=x^{2}+3x$$
$$x_{0}=-\frac{3}{2}=-1,5$$
$$y_{0}=(-1,5)^{2}+3(-1,5)=-2,25$$
$$m=-6,25$$ - 1точка
$$m\in(-6,25;-2,25)$$ - 2 точки
$$m=-2,25$$ - 3 точки
$$m=0$$ -3 точки
$$m\in(0;+\infty)$$ - 2 точки $$\Rightarrow$$
$$m\in[-6,25;-2,25]\cup[0;+\infty)$$
Задание 4801
Постройте график функции $$y=|x^{2}-2|x|-3|$$ и определите, какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс.
Сначала необходимо раскрыть первый модуль:
1)Если подмодульное выражение больше или равно нулю: $$\left\{\begin{matrix}x\geq 0\\ y=|x^{2}-2x-3|\end{matrix}\right.$$
Рассмотрим, когда подмодульное второе равно нулю: $$x_{1}=3 ; x_{2}=-1$$. Получаем, что на промежутках $$(-\infty ;-1)\cup (3;+\infty)$$ оно положительное, а при $$x\in (-1;3)$$ отрицательное. То есть мы получаем при $$x\geq 0$$: $$\begin{cases}y=x^{2}-2x-3 & \text{ if } x\in (-\infty ;-1)\cup (3;+\infty) \\ y=-x^{2}+2x+3 & \text{ if } x\in (-1;3)\end{cases}$$
В точках -1 и 3 значения будут одинаковы, потому нет разницы к какой части их присоединить
2)Если подмодульное выражение меньше нуля: $$\left\{\begin{matrix}x< 0\\ y=|x^{2}+2x-3|\end{matrix}\right.$$
Рассмотрим, когда подмодульное второе равно нулю: $$x_{1}=-3 ; x_{2}=1$$. Получаем, что на промежутках $$(-\infty ;-3)\cup (1;+\infty)$$ оно положительное, а при $$x\in (-3;1)$$ отрицательное. То есть мы получаем при $$x< 0$$: $$\begin{cases}y=x^{2}+2x-3 & \text{ if } x\in (-\infty ;-3)\cup (1;+\infty) \\ y=-x^{2}-2x+3 & \text{ if } x\in (-3;1)\end{cases}$$
В точках -3 и 1 значения будут одинаковы, потому нет разницы к какой части их присоединить
Далее необходимо построить графики четырех представленных парабол и оставить только те их части, которые даются по промежуткам:
Как видим по графику наибольшее количество общих точек составит 6 штук ($$y\in (3;4)$$)
Задание 4896
Постройте график функции $$y=2x|x|+x^{2}-6x$$ и определите, при каких значениях m прямая $$y=m$$ имеет с графиком более двух общих точек.
Задание 4990
Постройте график функции $$\frac{(x^{2}+x)\cdot|x|}{x+1}$$ и определите, при каких значениях а прямая $$y=a$$ не имеет с графиком ни одной общей точки.
Задание 5173
Постройте график функции $$y=\frac{(x^{2}+6,25)(x-1)}{1-x}$$ и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Задание 5223
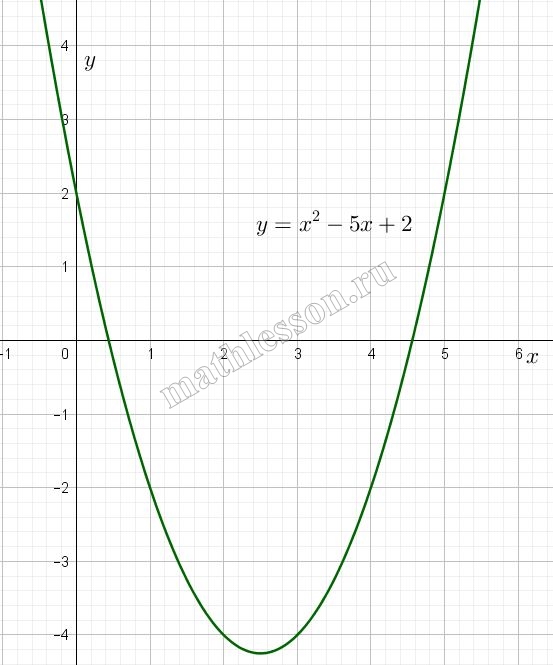
Постройте график функции $$y=|x^{2}-5x+2|$$ . Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

Задание 5366
Постройте график функции $$y=|x^{2}+6x+5|$$ и определите, при каких значениях а прямая $$y=a$$ имеет с графиком три общие точки.
Рассмотрим график функции $$y_{1}=x^{2}+6x+5$$. Искомый будет отличаться от данного тем, что та часть параболы, которая находится под осью Ох симметрично отобразиться относительно оси Ох (в силу того, что модуль все отрицательные значения сделает положительными). Найдем вершину параболы: $$x_{0}=-\frac{b}{2a}=-\frac{6}{2}=-3$$ , $$y_{1}(3)=(-3)^{2}+6*(-3)+5=-4$$. Найдем еще несколько значений для функции $$y_{1}$$: $$y_{1}(-2)=-3 ; y_{1}(-1)=0 ; y_{1}(0)=5$$.
График квадратичной функции симметричен относительно оси $$x=x_{0}$$, в нашем случае относительно $$x=-3$$. Начертим график функции $$y_{1}$$:
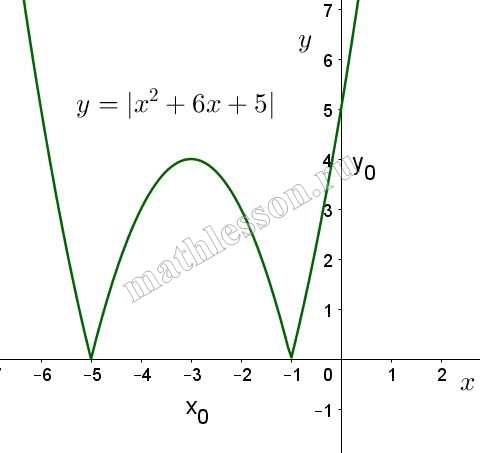
Отобразим симметрично относительно оси Ох ту часть параболы, которая располагается под осью Ох и получим график функции $$y=|x^{2}+6x+5|$$:
Очевидно, что прямая параллельная оси Оу будет иметь три точки пересечения с графиком данной функции при $$a=4$$: