ОГЭ
Задание 2672
Через середину M стороны BC параллелограмма ABCD, площадь которого равна 1, и вершину A проведена прямая, пересекающая диагональ BD в точке O. Найдите площадь четырёхугольника OMCD.
|
1) $$\bigtriangleup BOM\sim \bigtriangleup AOD$$; $$\frac{BM}{AD}=\frac{1}{2}$$ $$\Rightarrow$$ $$\frac{S_{BOM}}{S_{AOD}}=\frac{1}{4}$$ |
 |
2) Пусть $$S_{BOM}=S_{1}$$; $$S_{AOD}=S_{2}$$; $$S_{ABO}=S_{3}$$ $$\Rightarrow S_{AOD}=4S_{BOM}=4S_{2}$$; $$S_{ABD}=\frac{1}{2}S_{ABCD}=\frac{1}{2}$$; $$S_{ABM}=\frac{1}{2}\cdot AH\cdot BM=\frac{1}{2}\cdot \frac{1}{2}\cdot BC\cdot BM=\frac{1}{4}S_{ABCD}=\frac{1}{4}$$
3) $$\left\{\begin{matrix}S_{1}+S_{3}=\frac{1}{4}\\S_{3}+S_{2}=\frac{1}{2}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}S_{1}+S_{3}=\frac{1}{4}\\S_{3}+4S_{1}=\frac{1}{2}\end{matrix}\right.$$ (вычтем из второго первое) $$3S_{1}=\frac{1}{4}\Rightarrow S_{1}=\frac{1}{12}$$ $$S_{2}=4\frac{1}{12}=\frac{1}{3}$$ $$\Rightarrow$$ $$S_{3}=\frac{1}{4}-S_{1}=\frac{1}{4}-\frac{1}{12}=\frac{1}{6}$$ $$S_{1}+S_{2}+S_{3}=\frac{1}{12}+\frac{1}{3}+\frac{1}{6}=\frac{1+4+2}{12}=\frac{7}{12}=S_{ABMD}$$ $$S_{MOCD}=1-S_{ABMD}=1-\frac{7}{12}=\frac{5}{12}$$
Задание 2776
На боковой стороне трапеции выбрана точка, делящая эту сторону в отношении 3:1, считая от вершины меньшего основания. Прямая, проходящая через эту точку параллельно основаниям, делит площадь трапеции в отношении 2:1, считая о меньшего основания. В каком отношении делит площадь трапеции её средняя линия?
|
$$\frac{S_{BMLC}}{S_{AMLD}}=\frac{2}{1}$$ 1) Пусть $$BC=x$$; $$AD=y$$; $$BZ=h$$ $$\Rightarrow$$ $$BR=\frac{3h}{4}$$; $$RZ=\frac{h}{4}$$; $$AZ+ND=y-x$$ $$\Rightarrow$$ $$MR+IL=\frac{3}{4}(y-x)$$ $$\Rightarrow$$ $$ML=x+\frac{3}{4}(y-x)=\frac{x+3y}{4}$$ 2) $$\left.\begin{matrix}S_{BMLC}=\frac{x+\frac{x+3y}{4}}{2}\cdot \frac{3h}{4}=\frac{(5x+3y)\cdot 3h}{32}\\S_{AMLD}=\frac{\frac{x+3y}{4}+y}{2}\cdot \frac{h}{4}=\frac{(x+7y)\cdot h}{32}\end{matrix}\right\}$$ $$\Rightarrow$$ $$\frac{S_{BMLC}}{S_{AMLD}}=\frac{15x+9y}{x+7y}=\frac{2}{1}$$ $$\Rightarrow$$ $$15x+9y=2x+14y$$ $$\Rightarrow$$ $$y=\frac{13x}{5}=2,6x$$ 3) $$\left.\begin{matrix}S_{BCKH}=\frac{x+\frac{x+y}{2}}{2}\cdot \frac{h}{2}=\frac{(3x+y)\cdot h}{8}\\S_{MCDA}=\frac{\frac{x+y}{2}+y}{2}\cdot \frac{h}{2}=\frac{(x+3y)\cdot h}{8}\end{matrix}\right\}$$ $$\Rightarrow$$ $$\frac{S_{BCKH}}{S_{MCDA}}=\frac{3x+y}{x+3y}=\frac{3x+2,6x}{x+7,8x}=\frac{5,6x}{8,8x}=\frac{7}{11}$$ |
Задание 2930
В трапеции АВСD на продолжении основания ВС взята точка М таким образом, что прямая АМ отсекает от трапеции АВСD треугольник, площадь которого в 4 раза меньше площади трапеции АВСD. Найдите длину отрезка СМ, если АD=8, ВС=4.
Решение временно отсутствует, можете найти его в моем видео-разборе ( вначале варианта )
Задание 3846
В трапеции ABCD основания AD и ВС равны 6см и 10см соответственно. На продолжении ВС выбрана такая точка М, что прямая АМ отсекает от площади трапеции 1/4 её часть. Найдите длину отрезка СМ.
1) Пусть $$AH=h$$ - высота
$$S_{ABCD}=\frac{BC+AD}{2}\cdot AH=\frac{6+10}{2}\cdot h=h$$
тогда $$S_{AKD}=\frac{1}{2}AD\cdot x$$, х - высота
$$S_{AKD}=KM$$
$$S_{AKD}=\frac{1}{2}\cdot6\cdot x=3x=\frac{1}{4}S_{ABCD}=2h$$
$$x=\frac{2h}{3}$$
2) $$LK+KM=h$$ $$\Rightarrow$$ $$LK=\frac{h}{3}$$ - высота $$\bigtriangleup CMK$$
3) $$\bigtriangleup AKD\sim\bigtriangleup CMK$$ по трем углам $$\Rightarrow$$
$$\frac{AD}{CM}=\frac{KM}{KL}=\frac{2h}{3}\div\frac{h}{3}=\frac{2}{1}$$
$$CM=\frac{1}{2}AD=\frac{1}{2}\cdot6=3$$
Задание 3997
Продолжение сторон KN и LM выпуклого четырехугольника KLMN пересекаются в точке P, а продолжения сторон KL и LM – в точке Q. Отрезок PQ перпендикулярен биссектрисе угла KQN. Найти длину стороны KL, если KQ=12, NQ=8, а площадь четырехугольника KLMN равна площади треугольника LQM.
1) Постороим через К прямую $$m\parallel QP$$
Пусть $$ON\cap m=A$$; $$QB\cap m=B$$ (QB - биссектриса);
$$QL\cap m=K$$; $$PL\cap m=C$$
2) $$\bigtriangleup KAN\sim\bigtriangleup QNP$$; $$QA=QK=12$$ $$\Rightarrow$$
$$AN=AQ-QN=12-8=4$$; $$\frac{AN}{QN}=\frac{AK}{QP}=\frac{4}{8}=\frac{1}{2}$$
3) Пусть $$QK=xQL$$ $$\Rightarrow$$
$$KL=QK-QL=(x-1)QL$$
$$\bigtriangleup CKL\sim\bigtriangleup QLP$$ $$\Rightarrow$$
$$\frac{CK}{QP}=\frac{KL}{LQ}=\frac{(x-1)LQ}{LQ}$$ $$\Rightarrow$$
$$CK=QP(x-1)$$
4) Пусть $$AQ=yQM$$ $$\Rightarrow$$
$$AM=AQ-QM=yQM-QM=QM(y-1)$$
$$\bigtriangleup CAM\sim\bigtriangleup QMP$$ $$\Rightarrow$$
$$\frac{AC}{PQ}=\frac{AM}{MQ}=\frac{QM(y-1)}{QM}$$ $$\Rightarrow$$
$$AC=PQ(y-1)$$
$$AK=\frac{1}{2}PQ$$
$$AK=AC-CK$$ $$\Rightarrow$$
$$\frac{1}{2}PQ=(y-1)PQ-(x-1)PQ$$ $$\Leftrightarrow$$
$$\frac{1}{2}=y-1-x+1$$ $$\Leftrightarrow$$
$$\frac{1}{2}=y-x$$
5) $$S_{\bigtriangleup LQM}=S=\frac{1}{2}QL\cdot QM\cdot\sin Q=\frac{1}{2}\frac{QK}{x}\cdot\frac{AQ}{y}\sin Q$$
$$S_{\bigtriangleup QKN}=2S=\frac{1}{2}QK\cdot QN\cdot\sin Q$$
$$\frac{1}{2}QK\cdot QN\cdot\sin Q=2\cdot\frac{1}{2}\frac{QK}{x}\cdot\frac{AQ}{y}\sin Q$$
$$12\cdot8=2\cdot\frac{12}{x}\cdot\frac{12}{y}\Leftrightarrow$$
$$8=\frac{24}{xy}$$ $$\Leftrightarrow$$
$$xy=3$$
$$\left\{\begin{matrix}y=x+\frac{1}{2}\\xy=3\end{matrix}\right.$$
$$x(x+\frac{1}{2})=3$$
$$x^{2}+\frac{x}{2}-3=0$$
$$2x^{2}+x-6=0$$
$$D=1+48=49$$
$$x_{1}=\frac{-1+7}{4}=\frac{3}{2}$$
$$x_{2}<0$$
6) $$\Rightarrow$$: $$QL=\frac{QK}{\frac{3}{2}}=\frac{12\cdot2}{3}=8$$ $$\Rightarrow$$
$$KL=QK-QL=12-8=4$$
Задание 4537
Четырёхугольник ABCD вписан в окружность, его диагонали АС и BD пересекаются в точке F, причем AF : FС = 3 : 1, ВF : FD = 4 : 3, $$\cos\angle ADB=0,25$$. Найдите радиус окружности, описанной около треугольника ВАС, если АС = 4
1) $$AF\div FC=3\div1$$; $$AC=4$$ $$\Rightarrow$$ $$AF=3$$; $$FC=1$$
2) $$\angle CAD=\angle CBF$$; $$\angle BCA=\angle BDA$$ (опираются на одни дуги); $$\Rightarrow$$ $$\bigtriangleup BFC\sim\bigtriangleup AFD$$: пусть $$BF=4x$$; $$FD=3x$$, тогда $$k=\frac{BF}{AF}=\frac{CF}{FD}$$ $$\Rightarrow$$ $$\frac{4x}{3}=\frac{1}{3x}$$ $$\Rightarrow$$ $$4x^{2}=1$$ $$\Rightarrow$$ $$x=\frac{1}{2}$$ $$\Rightarrow$$ $$BF=2$$; $$FD=1,5$$
3) $$\frac{BC}{AD}=k=\frac{2}{3}$$ $$\Rightarrow$$ пусть $$BC=a$$ $$\Rightarrow$$ $$AD=1,5a$$. По теореме косинусов для $$\bigtriangleup ABC$$ и $$\bigtriangleup ABD$$: $$\left\{\begin{matrix}AB^{2}=BC^{2}+AC^{2}-2BC\cdot AC\cdot\cos\angle BCA\\AB^{2}=BD^{2}+AD^{2}-2BD\cdot AD\cdot\cos\angle BDA\end{matrix}\right.$$ Приравниваем их: $$a^{2}+16-2\cdot4\cdot a\cdot\frac{1}{4}=2,25a^{2}+12,25-2\cdot\frac{2}{3}a\cdot3,5\cdot\frac{1}{4}$$; $$1,25a^{2}+3,75a-0,625a=0$$; $$2a^{2}-a+6=0$$; $$a=2$$ $$\Rightarrow$$ $$b=\sqrt{4+16-2\cdot2\cdot4\cdot\frac{1}{4}}=4=AB$$
4) Из $$\bigtriangleup ABC$$: $$\frac{AB}{2\sin\angle BCA}=R$$, где R - радиус описанной окружности; $$\sin\angle BCA=\sqrt{1-\cos^{2}\angle BCA}=\sqrt{1-\frac{1}{16}}=\frac{\sqrt{15}}{4}$$; $$R=\frac{4}{2\cdot\frac{\sqrt{15}}{4}}=\frac{8}{\sqrt{15}}=\frac{8\sqrt{15}}{15}$$
Задание 4899
Стороны ромба EFGH являются гипотенузами прямоугольных равнобедренных треугольников EAF, FDG, GCH и HBE, причем все эти треугольники имеют общие внутренние точки с ромбом EFGH. Сумма площадей четырехугольника ABCD и ромба EFGH равна 12. Найдите CH.

Задание 5042
В выпуклом четырёхугольнике ABCD точка Е – точка пересечения диагоналей. Известно, что площадь каждого из треугольников АВЕ и DСЕ равна 1, площадь четырёхугольника АВСD не превосходит 4, АD = 3. Найдите длину стороны ВС.
1) $$S_{ABC}=S_{CED}=1$$ $$\Rightarrow$$ $$BE\cdot AE=CE\cdot ED$$ $$\Rightarrow$$ $$\frac{BE}{ED}=\frac{CE}{EA}$$; $$\angle BEC=\angle AED$$ $$\Rightarrow$$ $$\bigtriangleup BEC\sim\bigtriangleup AED$$ $$\Rightarrow$$ дана трапеция.
2) Пусть НМ - высота $$\Rightarrow$$ $$S_{BEC}=\frac{1}{2}BC\cdot HE$$; $$S_{AED}=\frac{1}{2}EM\cdot AD$$. Пусть $$EM=x$$ $$\Rightarrow$$ $$HE=kx$$, где $$k$$ - коэфф. подобия $$\Rightarrow$$ $$BC=k\cdot3$$ $$\Rightarrow$$
$$S_{BEC}+S_{AED}=\frac{1}{2}\cdot3k\cdot kx+\frac{1}{2}\cdot3x=\frac{1}{2}\cdot3x(k^{2}+1)\leq2$$ $$\Rightarrow$$ $$x(k^{2}+1)\leq\frac{4}{3}$$ $$(1)$$
$$S_{ABCD}=\frac{3k+3}{2}\cdot(kx+x)<4$$ $$\Rightarrow$$ $$x(k+1)^{2}\leq\frac{8}{3}$$ $$(2)$$
Поделим первое на второе: $$\frac{k^{2}+1}{(k+1)^{2}}\leq\frac{4}{3}\cdot\frac{3}{8}$$ $$\Leftrightarrow$$ $$\frac{k^{2}+1}{(k+1)^{2}}\leq\frac{1}{2}$$ $$\Leftrightarrow$$ $$2k^{2}+2\leq k^{2}+2k+1$$ $$\Leftrightarrow$$ $$k^{2}-2k+1\leq0$$ $$\Leftrightarrow$$ $$(k-1)^{2}\leq0$$ $$\Leftrightarrow$$ $$k=1$$ $$\Rightarrow$$ $$BC=1\cdot3=3$$
Задание 5369
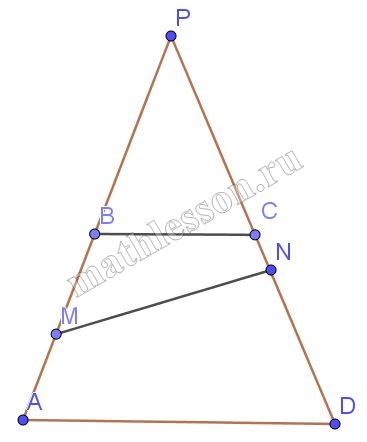
На боковой стороне АВ трапеции АВСD взята точка М таким образом, что АМ : МВ = 2 : 3. На противоположной стороне СD взята такая точка N, что отрезок MN делит трапецию на части, одна из которых по площади втрое больше другой. Найдите отношение CN : ND, если известно, что BC : AD = 1 : 2