ОГЭ
Задание 1975
В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.
По формуле площади треугольника $$S=\frac{1}{2}*10*5=25$$
Задание 1976
В треугольнике одна из сторон равна 10, другая равна $$10\sqrt{3}$$, а угол между ними равен 60°. Найдите площадь треугольника.
По формуле площади треугольника $$S=\frac{1}{2}10*10\sqrt{3}*\sin 60^{\circ}=75$$
Задание 1981
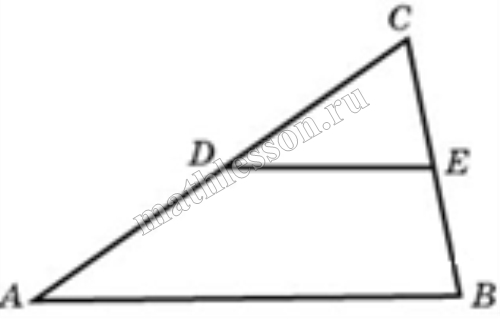
В треугольнике ABC отрезок DE — средняя линия. Площадь треугольника CDE равна 45. Найдите площадь треугольника ABC.
- Так как DE - средняя линия, то $$DE=\frac{1}{2}AC$$, но тогда $$S_{CDE}=\frac{1}{2}S_{ADC}$$ (у них одинаковая высота, но различные в два раза основания). То есть $$S_{ADC}=2*45=90$$, тогда $$S_{ADEC}=135$$
- Треугольники ABC и DBE подобны (по свойству средней линии), при это $$k=\frac{1}{2}$$ - коэффициент подобия, тогда $$\frac{S_{BDE}}{S_{ABC}}=k^{2}=\frac{1}{4}$$, тогда $$S_{BDE}=\frac{1}{4}S_{ABC}$$, следовательно, $$S_{ADEC}=\frac{3}{4}S_{ABC}$$. Получаем, что $$S_{ABC}=\frac{4}{3}S_{ADEC}=180$$
Задание 1982
Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.
Из формулы площади треугольника $$S=\frac{1}{2}*12*33=198$$
Задание 3402
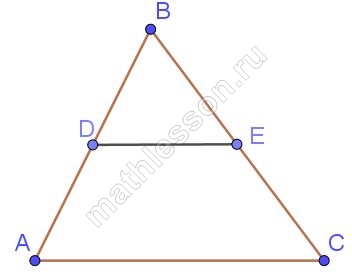
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 12. Найдите площадь треугольника ABC.
Т.к. DE - средняя линия, то $$k=\frac{1}{2}$$ $$\frac{S_{CDE}}{S_{ABC}}=k^{2}=\frac{1}{4}$$ $$\Rightarrow$$ $$S_{ABC}=4S_{CDE}=4\cdot12=48$$
Задание 4645
Найдите площадь треугольника, изображенного на рисунке:
$$S=\frac{1}{2}ah=0.5*60(32+11)=1290$$
Задание 6782
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 8. Найдите площадь треугольника ABC
$$\frac{DE}{AB}=\frac{1}{2}=k\Rightarrow$$ $$\frac{S_{DCE}}{S_{ABC}}=k^{2}=\frac{1}{4}\Rightarrow$$ $$S_{ABC}=8*4=32$$
Задание 6853
В равнобедренном треугольнике ABC АВ = ВС, AС = 24, cos A = 0,48. Найдите площадь треугольника АВС.
Опустим высоту (медиану) BH
1) $$AH=\frac{AC}{2}=12$$
2) $$AB=\frac{AH}{\cos A}=\frac{12}{0,48}=25$$
3) По формуле Герона: $$S=\sqrt{p(p-a)(p-b)(p-c)}$$; $$p=\frac{a+b+c}{2}$$
$$p=\frac{25+25+24}{2}=37$$
$$S=\sqrt{37*12*12*13}=12\sqrt{481}$$
Задание 6901
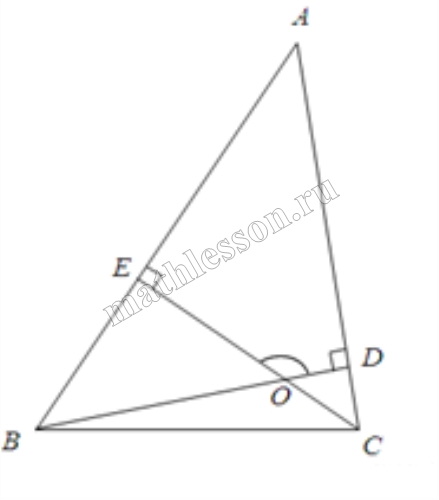
В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
$$S=\frac{1}{2} AH*BC=\frac{1}{2} AC*BM\Rightarrow$$ $$AH*BC=AC*BM$$
Пусть BC=15, AC=3, AH=1, тогда $$BM=\frac{AH*BC}{AC}=\frac{1*15}{3}=5$$
Задание 7156
Найдите площадь треугольника, изображенного на рисунке:
$$S=\frac{1}{2} ah$$ , где a-сторона треугольника , h- высота к ней проведенная $$\Rightarrow$$ $$S=\frac{1}{2}(32+11)*60=1290$$