ОГЭ
Задание 3102
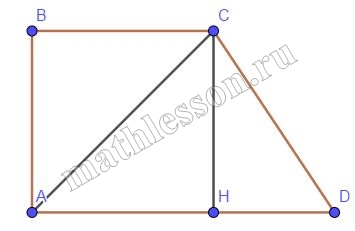
Длина средней линии трапеции равна 5 см, а длина отрезка, соединяющего середины оснований, равна 3 см. Найдите длину большего основания, если углы при нем равны 30º и 60º.
1) $$\angle H=180^{\circ}-\angle A-\angle D=180^{\circ}-60^{\circ}-30^{\circ}=90^{\circ}$$ $$\Rightarrow$$
$$\bigtriangleup AHD$$ - прямоугольный $$\Rightarrow$$
HL - медиана; HL=AL=LP
2) $$KZ=ZL=1,5$$; $$MZ=ZN=2,5$$
Пусть $$KC=x$$; $$LD=y$$ $$\Rightarrow$$ $$KH=HL-KL=y-3$$
3) $$\bigtriangleup HZN\sim \bigtriangleup HLD$$: $$\frac{HZ}{HL}=\frac{ZN}{LD}$$ $$\Leftrightarrow$$
$$\frac{y-1,5}{y}=\frac{2,5}{y}$$
$$y^{2}-1,5y=2,5y$$
$$y^{2}-4y=0$$
$$y=0$$ (не подходит) и $$y=4$$ $$\Rightarrow$$
$$AD=2\cdot4=8$$
Задание 3274
Середины двух соседних сторон и не принадлежащая им вершина ромба соединены друг с другом отрезками прямых. Найдите площадь получившегося треугольника, если сторона ромба равна 4 см, а острый угол равен 60°.
$$BH=DM=2$$ $$S_{\bigtriangleup ABH}=S_{\bigtriangleup ADM}=$$ $$=\frac{1}{2}\cdot2\cdot4\cdot\sin120^{\circ}=4\cdot\frac{\sqrt{3}}{2}=2\sqrt{3}$$ $$S_{\bigtriangleup CMH}=\frac{1}{2}\cdot2\cdot2\cdot\sin60^{\circ}=\sqrt{3}$$ $$S_{ABCD}=4\cdot4\cdot\sin120^{\circ}=\frac{16\sqrt{3}}{2}=8\sqrt{3}$$ $$S_{AHM}=8\sqrt{3}-2\cdot2\sqrt{3}-\sqrt{3}=3\sqrt{3}$$
Задание 3844
Боковые стороны AB и CD трапеции ABCD равны соответственно 18 и 30, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
1) Достроим $$DL$$ до пересечения с $$BC$$
$$DL\cap BC=M$$
2) $$\bigtriangleup MCD$$ - равнобедренный, т.к. $$\angle LDA=\angle LDC$$ ($$DL - (бисектрисса)
($$\angle BML=\angle ALD$$ - накрестлежащие)
3) $$CM=CD=30$$ $$\Rightarrow$$ $$BM=30-BC=27$$
4) $$\bigtriangleup MBL=\bigtriangleup LDA$$ ($$LB=LA$$; $$\angle MBL=\angle LAD$$; $$\angle MLB=\angle ALD$$)
$$\Rightarrow$$ $$AD=MB=27$$
5) опустим $$BH\perp CAD$$; $$CK\perp AD$$
$$BH=CK=y$$, тогда $$HK=KB=3$$
Пусть $$AH=x$$, тогда $$KD=27-x-3=24-x$$
Распишем т. Пифагора для $$\bigtriangleup ABH$$ и $$\bigtriangleup CKD$$
$$\left\{\begin{matrix}x^{2}+y^{2}=18^{2}\\(24-x)^{2}+y^{2}=30^{2}\end{matrix}\right.$$
$$(24-x)^{2}-x^{2}=30^{2}-18^{2}$$
$$576-48x+x^{2}-x^{2}=576$$
$$-48x=0$$
$$x=0$$ $$\Rightarrow$$
$$AB\perp AD$$
$$S_{ABCD}=\frac{3+27}{2}\cdot18=30\cdot9=270$$
Задание 3995
В прямоугольную трапецию вписана окружность. Найдите её радиус, если основания трапеции 2 см и 3 см.
1) Пусть К - точка каасния АВ и окружности
2) Пусть r - радиус окружности $$BK=KA=r$$ $$\Rightarrow$$ $$BA=2r$$
3) По свойству описанного четырехугольника: $$AB+CD=BC+AD$$ $$\Rightarrow$$
$$2r+CD=2+3=5$$ $$\Rightarrow$$
$$CD=5-2R$$
4) Опустим $$CC_{1}\perp AD$$ $$\Rightarrow$$
$$CC_{1}=AB=2r$$
По теореме Пифагора: $$CC_{1}^{2}+C_{1}D^{2}=CD^{2}$$
$$C_{1}D=AD-BC=3-2=1$$
$$(2r)^{2}+1^{2}=(5-2r)^{2}$$
$$4r^{2}+1=25-20r+4r^{2}$$
$$20r=24$$ $$\Rightarrow$$ $$r=1,2$$
Задание 4059
В равнобедренной трапеции диагональ длиной 3 см образует угол $$45^{\circ}$$ с основанием. Найдите площадь трапеции.
1) Построим BH и CM $$\perp AD\Rightarrow$$
$$\bigtriangleup BHD$$ - прямоугольный
$$\angle HDB=45^{\circ}\Rightarrow$$ ; $$\angle HBD=45^{\circ}\Rightarrow$$
$$BH=HD=x$$
$$BH^{2}+HD^{2}=BD^{2}$$
$$2x^{2}=9\Rightarrow x^{2}=\frac{9}{2}$$ $$\Rightarrow$$
$$x=\frac{3\sqrt{2}}{2}$$
2) $$BH=CM;AB=CD\Rightarrow$$
$$\bigtriangleup AHB=\bigtriangleup CMD$$ $$\Rightarrow$$
$$AH=MD=y$$ $$\Rightarrow$$
$$HM=\frac{3\sqrt{2}}{2}-y=BC$$
3) $$S_{ABCD}=\frac{AD+BC}{2}\cdot BH=$$
$$=\frac{y+\frac{3\sqrt{2}}{2}+\frac{3\sqrt{2}}{2}-y}{2}\cdot\frac{3\sqrt{2}}{2}=$$
$$=\frac{3\sqrt{2}}{2}\cdot\frac{3\sqrt{2}}{2}=\frac{9}{2}=4,5$$
Задание 4802
Площадь равнобедренной трапеции равна 96. Диагональ трапеции делит её тупой угол пополам. Длина меньшего основания равна 3. Найдите периметр трапеции.
Построим рисунок согласно условию задачи.
Задание 4870
В равнобедренной трапеции основания равны 12 см и 20 см, а диагонали взаимно перпендикулярны. Найдите площадь трапеции.
Задание 4944
Около окружности диаметром 15 описана равнобедренная трапеция с боковой стороной, равной 17. Найдите длину большего основания трапеции.
1) По свойству радиусов .проведенных в точку касания, диаметр и высота трапеции одинаковы, тогда, из треугольника CND по теореме Пифагора: $$ND=\sqrt{CD^{2}-CN^{2}}=\sqrt{17^{2}-15^{2}}=8=AK$$
2) По свойству четырехугольника, описанного около окружности имеем, что $$BC+AD=AB+CD$$. Пусть $$BC=KN=x$$, тогда $$x+8+x+8=17+17$$, тогда $$x=9$$, следовательно, $$AD=8+9+8=25$$
Задание 5040
Меньшее основание прямоугольной трапеции равно 12,5 см, а большая диагональ является биссектрисой угла при большем основании и равна 20 см. Найдите площадь трапеции.
1) $$\angle BDC=\angle ADB$$ (BD - биссект.); $$\angle CDB=\angle BDA$$ (накрестлежащие); $$\Rightarrow$$ $$\angle CBD=\angle BCD$$ $$\Rightarrow$$ $$BC=CD=12,5$$
2) $$CH$$ - высота, тогда $$AH=HD=12,5$$. Пусть $$AB=CH=x$$, $$HD=y$$,тогда: из $$\bigtriangleup CHD$$ и $$\bigtriangleup ABD$$: $$\left\{\begin{matrix}x^{2}+y^{2}=(12,5)^{2}\\x^{2}+(12,5+y)^{2}=20^{2}\end{matrix}\right.$$
$$20^{2}-(12,5+y)^{2}+y^{2}=12,5^{2}$$; $$400-12,5^{2}-25y-y^{2}+y^{2}-12,5^{2}=0$$; $$400-312,5=25y$$; $$y=3,5$$ $$\Rightarrow$$ $$x=\sqrt{400-256}=12$$
3) $$S=\frac{12,5+12,5+3,5}{2}\cdot12=171$$
Задание 5087
Основания трапеции равны 6 см и 18 см. Через точку пересечения диагоналей проведена прямая, параллельная основаниям, до пересечения с боковыми сторонами. Найдите длину отрезка этой прямой.
1) $$\bigtriangleup BOC\sim\bigtriangleup AOD$$ $$\Rightarrow$$ $$\frac{OC}{AO}=\frac{BC}{AD}=\frac{6}{18}=\frac{1}{3}$$
2) т.к. $$\bigtriangleup AOM\sim\bigtriangleup ABC$$ $$\Rightarrow$$ $$\frac{MO}{BC}=\frac{AO}{AC}$$; $$\frac{AO}{AC}=\frac{AO}{AO+OC}$$; $$OC=\frac{1}{3}AO$$ $$\Rightarrow$$ $$\frac{AO}{AO+OC}=\frac{AO}{AO+\frac{1}{3}AO}=\frac{3}{4}$$ $$\Rightarrow$$ $$MO=\frac{3}{4}BC=4,5$$
3) т.к. $$\bigtriangleup OCN\sim\bigtriangleup ACD$$ $$\Rightarrow$$ $$\frac{ON}{AD}=\frac{OC}{AC}$$; $$\frac{OC}{AC}=\frac{OC}{OC+3OC}=\frac{1}{4}$$ $$\Rightarrow$$ $$ON=\frac{1}{4}AD=4,5$$ $$\Rightarrow$$ $$MN=9$$
Задание 5415
Высота прямоугольной трапеции в три раза больше меньшего основания, а большее основание равно 5. Найдите площадь трапеции, если её диагональ является биссектрисой угла при меньшем основании.
1)AC-биссектриса $$\Rightarrow \angle BCA=\angle DCA;$$
$$\angle DAC=\angle BCA$$(накрест)$$\Rightarrow \angle DCA=\angle DAC\Rightarrow AD=CD=5;$$
2)$$CH||AB\Rightarrow AH=BC=x\Rightarrow HD=5-x$$ $$CH=3*x \Rightarrow \Delta CHD:5^{2}=\left ( 5-x \right )^{2}+3*x ^{2};$$
$$25=25-10x +x ^{2}+9x ^{2}\Rightarrow$$ $$10x ^{2}-10x =0\Rightarrow$$ $$10x \left ( x -1 \right )=0\Rightarrow$$$$x =0; x =1;$$
3)$$S=\frac{5+1}{2}*3=9;$$
Задание 5525
Основания равнобедренной трапеции равны 8 и 18, а периметр равен 56. Найдите площадь трапеции.
1) Пусть $$AB=18$$; $$DC=8$$ $$\Rightarrow$$ $$AD=CB=\frac{56-(18+8)}{2}=15$$
2) Пусть $$CH$$ и $$DM\perp AB$$ $$\Rightarrow$$ $$MN=DC=8$$; $$AD=CB$$; $$DM=CH$$ $$\Rightarrow$$ $$\bigtriangleup AMD=\bigtriangleup CHB$$ (по гипотенузе и катету) $$\Rightarrow$$ $$AM=HB=\frac{18-8}{2}=5$$
3) $$CH=\sqrt{CB^{2}-HB^{2}}=\sqrt{15^{2}-5^{2}}=\sqrt{200}=10\sqrt{2}$$
4) $$S_{ABCD}=\frac{AB+CD}{2}\cdot CH=\frac{18+8}{2}\cdot10\sqrt{2}=130\sqrt{2}$$
Задание 5526
В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 8.
1) т.к. окружность вписана, то $$AB+CD=BC+AD$$, но $$ABCD$$ - параллелограм $$\Rightarrow$$ $$AB+CD$$; $$AD=BC$$ $$\Rightarrow$$ $$2AB=2BC$$ $$\Rightarrow$$ $$AB=BC$$ $$\Rightarrow$$ $$ABCD$$ - ромб
2) $$P_{ABCD}=4\cdot AB=4\cdot8=32$$
Задание 5527
Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 3. Найдите высоту ромба.
1) $$ABCD$$ - ромб $$\Rightarrow$$ $$AD=CD=12+3=15$$
2) $$\bigtriangleup AHD$$ - прямоугольный $$\Rightarrow$$ $$AH=\sqrt{AD^{2}-DH^{2}}=\sqrt{15^{2}-12^{2}}=9$$
Задание 5528
Периметр прямоугольника равен 56, а диагональ равна 27. Найдите площадь этого прямоугольника.
1) Пусть $$AD=x$$, $$DC=y$$, тогда $$2(x+y)=56$$ $$\star$$
2) $$\bigtriangleup ADC$$ - прямоугольный $$\Rightarrow$$ $$AD^{2}+CD^{2}=AC^{2}$$. С учетом $$\star$$: $$\left\{\begin{matrix}x+y=28&\\x^{2}+y^{2}=27^{2}&\end{matrix}\right.$$ $$\Rightarrow$$ $$\left\{\begin{matrix}x^{2}+y^{2}=784&\\x^{2}+y^{2}=729^{2}&\end{matrix}\right.$$ Подставим из второго в первое: $$729+2xy=784$$ $$\Rightarrow$$ $$2xy=55$$ $$\Rightarrow$$ $$xy=27,5$$
Задание 5529
Прямая, параллельная основаниям MP и NK трапеции MNKP, проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны MN и KP в точках A и B соответственно. Найдите длину отрезка AB, если MP=40 см, NK=24 см.
1) Пусть $$NP\cap MK=H$$; $$NK\parallel MP$$ $$\Rightarrow$$ $$\bigtriangleup NHK\sim\bigtriangleup MHP$$; $$\frac{NK}{MP}=\frac{24}{40}=\frac{3}{5}=\frac{NH}{HP}=\frac{HK}{HM}$$ $$\Rightarrow$$ $$\frac{MK}{MN}=\frac{8}{5}=\frac{NP}{HP}$$
2) $$AB\parallel NK$$ $$\Rightarrow$$ $$\bigtriangleup AHM\sim\bigtriangleup MNK$$ $$\Rightarrow$$ $$\frac{NK}{AH}=\frac{MK}{MH}=\frac{8}{5}$$ $$\Rightarrow$$ $$AH=\frac{24\cdot5}{8}=15$$. Аналогично $$\bigtriangleup HBP\sim\bigtriangleup NKP$$ и $$\frac{NK}{HB}=\frac{NP}{HP}=\frac{8}{5}$$ $$\Rightarrow$$ $$HB=15$$ $$\Rightarrow$$ $$AB=30$$
Задание 5530
Диагонали AC и BD трапеции ABCD пересекаются в точке O. Площади треугольников AOD и BOC равны соответственно 16 см2 и 9 см2. Найдите площадь трапеции.
1) $$BC\parallel AD$$ $$\Rightarrow$$ $$\angle BCO=\angle OAD$$; $$\angle CBO=\angle ODA$$ (накрестлежащие) $$\Rightarrow$$ $$\bigtriangleup BOC\sim\bigtriangleup AOD$$
2) $$\frac{S_{BOC}}{S_{AOD}}=\frac{9}{16}$$ см2 $$\Rightarrow$$ $$\frac{BC}{AD}=\sqrt{\frac{9}{16}}=\frac{3}{4}$$ (отношение площадей подобных фигур) $$\Rightarrow$$ $$BO=3x$$ $$\Rightarrow$$ $$DO=4x$$; $$CO=3y$$ $$\Rightarrow$$ $$AO=4y$$
3) $$\angle BOC=\alpha$$ $$\Rightarrow$$ $$\angle BOA=180^{\circ}-\alpha$$ $$\Rightarrow$$ $$\sin\angle BOC=\sin\angle BOA$$ (смежные), $$\angle BOA=\angle COD$$; $$\angle BOC=\angle AOD$$ (вертикальные)
4) $$S_{BOA}=\frac{1}{2}\cdot BO\cdot OA\cdot\sin\angle BOA=\frac{1}{2}\cdot3x\cdot4y\cdot\sin\alpha=6xy\sin\alpha$$; $$S_{COD}=\frac{1}{2}\cdot CO\cdot OD\cdot\sin\angle COD=\frac{1}{2}\cdot3y\cdot4x\cdot\sin\alpha=6xy\sin\alpha=S_{BOA}$$; $$S_{BOC}=\frac{1}{2}\cdot BO\cdot OC\cdot\sin\angle BOC=\frac{1}{2}\cdot3x\cdot3y\cdot\sin\alpha=9$$ $$\Rightarrow$$ $$xy\sin\alpha=2$$ $$\Rightarrow$$ $$S_{BOA}=S_{COD}=12$$
5) $$S_{ABCD}=9+2\cdot12+16=49$$
Задание 5531
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
1) Пусть $$CH\perp AD$$ $$\Rightarrow$$ $$\angle HCD=90^{\circ}-\angle CDH=30^{\circ}$$ $$\Rightarrow$$ $$HD=CD\cdot\sin30^{\circ}=\frac{x}{2}$$;
2) Пусть $$BM\perp AM$$ $$\Rightarrow$$ $$MH=BC=x$$ $$\Rightarrow$$ $$AM=2x-x-\frac{x}{2}=\frac{x}{2}=HD$$ $$\Rightarrow$$ $$AM=HD$$; $$BM=CH$$ $$\Rightarrow$$ $$\bigtriangleup AMB=\bigtriangleup CAD$$ (по двум катетам) $$\Rightarrow$$ $$CD=AB=2=x$$ $$\Rightarrow$$ $$AM=1$$ $$\Rightarrow$$ по т. Пифагора из $$\bigtriangleup ABM$$: $$BM=\sqrt{AB^{2}-AM^{2}}=\sqrt{3}$$
3) $$S_{ABCD}=\frac{BC+AD}{2}\cdot BM=\frac{2+4}{2}\cdot\sqrt{3}=3\sqrt{3}$$
Задание 5532
В выпуклом четырёхугольнике ABCD длина отрезка, соединяющего середины сторон AB и , CD равна одному метру. Прямые BC и AD перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей AC и BD.
1) Пусть $$L$$ - середина $$AC$$; $$K$$ - середина $$BD$$ $$\Rightarrow$$ $$ML$$ - средняя линия $$\bigtriangleup ABC$$, а $$KN$$ - $$\bigtriangleup DBC$$ $$\Rightarrow$$ $$LM=\frac{BC}{2}=NK$$ и $$LM\parallel BC\parallel NK$$ $$\Rightarrow$$ $$LMNK$$ - параллелограм
2) Аналогично, $$LN$$ - средняя линия $$\bigtriangleup CDA$$; $$MK$$ - $$\bigtriangleup ABD$$ $$\Rightarrow$$ $$LN=\frac{AD}{2}=MK$$, $$LN\parallel AD\parallel MK$$ $$\Rightarrow$$ $$LMNK$$ - прямоугольник $$\Rightarrow$$ $$MN=LK=1$$
Задание 5533
Каждое основание AD и BC трапеции ABCD продолжено в обе стороны. Биссектрисы внешних углов A и B этой трапеции пересекаются в точке K, биссектрисы внешних углов C и D пересекаются в точке E. Найдите периметр трапеции ABCD, если длина отрезка KE равна 28
1) Сумма внешних углов $$A$$ и $$B$$ равна $$180^{\circ}$$ (т.к. $$BC\parallel AD$$), а т.к. $$AK$$ и $$BK$$ - биссектрисы, то $$\angle KAB+\angle KBA=90^{\circ}$$. Кроме того $$K$$ равноудалена от $$BC$$ и $$AB$$ и от $$AD$$ и $$AB$$, т.к. лежит на биссектрисах.
2) Аналогично $$\bigtriangleup CED$$ - прямоугольный и $$E$$ равноудалена от $$BC$$ и $$AD$$
3) Пусть $$KE\cap AB=M$$; $$KE\cap CD=N$$, тогда из п.1 и п.2 $$MN$$ - средняя линия $$\Rightarrow$$ $$MN=\frac{BC+AD}{2}$$
4) $$KM$$ - медиана $$\bigtriangleup KBA$$, а он прямоугольный $$\Rightarrow$$ $$KM=AM=MB=\frac{AB}{2}$$, аналогично $$EN=\frac{CD}{2}$$
5) $$KE=KM+MN+NE=\frac{AB+BC+CD+AD}{2}$$ $$\Rightarrow$$ $$P_{ABCD}=2KE=48$$
Задание 6071
В прямоугольную трапецию с основаниями 5 см и 6 см вписана окружность. Найдите площадь этой трапеции.
1) BC=5; CD=6; опустим $$CH\perp AD$$ , тогда $$HD=6-5=1$$.
2) Пусть AB=x, тогда CH=x Пусть CD=y , тогда из $$\Delta CHD: x^{2}+1^{2}=y^{2}$$
По свойству описанного многоугольника : $$5+6=x+y$$. Тогда:
$$\left\{\begin{matrix}x^{2} +1=y^{2}\\x+y-11 & &\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}x^{2}+1=(11-x)^{2} \\y=11-x\end{matrix}\right.$$
3)$$S=\frac{5+6}{2}*\frac{60}{11}=30$$.
Задание 6118
Диагональ равнобедренной трапеции делит пополам угол при её основании. Найдите большее основание трапеции, если её меньшее основание равно 5 см, а высота - 4,8 см.
- $$\angle BAC=\angle CAD$$ (AC - биссектрисса)
- $$\angle CAD=\angle BCA$$ (накрест лежащие при параллельных), следовательно треугольник ABC - равнобедренный и $$AB=BC=CD=5$$
- Проведем перпендикуляры BM и CH к AD. Из треугольника CHD: $$HD=\sqrt{CD^{2}-CH^{2}}=\sqrt{5^{2}-4,8^{2}}=1,4$$
- $$AM=HD=1,4$$, тогда $$AD=5+1,4*2=7,8$$
Задание 6213
Около круга радиуса 2 см описана равнобедренная трапеция с острым углом 30. Найдите длину средней линии трапеции.
- Пусть BH-высота, тогда BH=2ч=4
- из $$\Delta ABH$$: $$AB=BH \sin A=\frac{4}{\frac{1}{2}}=8=CD$$
- т.к. $$AB+CD=BC+AD$$(свойство описанного выпуклого четырехугольника) , то $$BC+AD=16$$, тогда средняя линия $$\frac{16}{2}=8$$
Задание 6309
В параллелограмме ABCD биссектриса тупого угла B пересекает сторону АD в точке К. Найти периметр параллелограмма, если АВ = 12 и АК:КD = 4:3
a) Пусть $$K\in AD$$(внутри), тогда:
1) $$\angle ABK=\angle CBK$$(BK-биссектриса); $$\angle CBK=\angle AKB$$(накрест лежащие) $$\Rightarrow \Delta ABK$$-равнобедренный и $$AB = AK$$
2) пусть $$AB=4x =12\Rightarrow x=3, KD=3x=9$$$$\Rightarrow AD=21$$
3) $$P_{ABCD}=2(12+21)=66$$
b) вне AD. Аналогично $$AK=AB=12$$. Пусть $$DK=3x$$, тогда AK=4x и AD=x. Получаем $$4x=12\Rightarrow x=3$$ и $$P_{ABCD}=2(12+3)=30$$
Задание 6403
В равнобедренную трапецию АВСD с основаниями ВС = 18 и AD = 32 вписан круг. Найдите площадь трапеции.
1) $$BC+AD=AB+CD=18+32=50$$ ( по свойству описанного четырехугольника ), тогда AB=CD=25
2) Пусть $$BH\left | \right |CM \perp AD$$, тогда $$AH=MD=\frac{AD-BC}{2}=7$$
3) По т. Пифагора $$\Delta ABH$$: $$BH=\sqrt{25^{2}-7^{2}}=24$$
4) $$S=\frac{18+32}{2}*24=600$$
Задание 6450
В равнобедренной трапеции с основаниями 10 и 26 см диагональ является биссектрисой острого угла. Найдите площадь трапеции.
1) $$\angle BAC=\angle CAD$$ (AC-бисссектриса), $$\angle CAD=\angle BCA$$ ( накрест лежащие ), тогда $$\angle BAC=\angle ACA$$, следовательно, $$\Delta ABC$$ - равнобедренный, и AB=BC=10
2) Пусть BH=CM - высота, тогда $$AH=MD=\frac{AD-BC}{2}=8$$
3) из $$\Delta ABH:$$ $$BH=\sqrt{AB^{2}-AB^{2}}=6$$
4) $$S_{ABCD}=\frac{10+26}{2}*6=108$$
Задание 6505
Средняя линия трапеции равна 10 и делит площадь трапеции в отношении 3:5. Найти длины оснований этой трапеции.
1) Пусть BC=x , тогда , т.к. MN-средняя линия , то BC+AD=2MN $$\Rightarrow$$ AD=2MN-BC=20-x
2) Пусть BK –высота и BH=HK=y. Тогда :
$$\frac{x+10}{2}*y=S_{MBCN}$$
$$\frac{10+20-x}{2}*y=S_{AMND}$$
Получаем:
$$\frac{\frac{10+x}{2}*y}{\frac{30-x}{2}*y}=\frac{3}{5}\Leftrightarrow$$ $$\frac{10+x}{30-}=\frac{3}{5}\Leftrightarrow$$ $$50+5x=90-3x\Leftrightarrow$$ $$8x=40\Leftrightarrow x=5$$, тогда: BC=5, AD=15
Задание 6741
Диагонали параллелограмма АВСD пересекаются в точке О. В треугольнике АОВ АВ = 6 см, медиана ОК = 4 см. Найдите периметр параллелограмма АВСD.
1) Построим медиану в $$\Delta DOC$$: $$DL=LC=\frac{CD}{2}$$$$\Rightarrow$$ $$DL=AK$$, но $$DL\left | \right |AK$$$$\Rightarrow$$ $$AKLD$$ - параллелограмм $$\Rightarrow$$ $$AD=KL$$
2) $$\Delta KBO=\Delta ODL$$ ($$DC=KB$$; $$\angle BKO=\angle OLD$$; $$\angle KDO=\angle ODC$$ (накрест лежащие)) $$\Rightarrow$$ $$KO=OL=4$$
3) $$P=(6+8)*2=18$$
Задание 6955
Боковая сторона неравнобедренной трапеции равна 12 см и образует с большим основанием угол 60. Основания трапеции равны 16 см и 40 см. Найдите площадь трапеции.
1) Пусть $$BH\perp AD\Rightarrow$$ из $$\Delta ABH$$: $$BH=AB \sin A=12*\frac{\sqrt{3}}{2}=4\sqrt{3}$$
2) $$S_{ABCD}=\frac{BC+AD}{2}*BH=$$$$\frac{16+40}{2}*4\sqrt{3}=112\sqrt{3}$$
Задание 7089
Перпендикуляр, опущенный из вершины параллелограмма на его диагональ, делит ее на отрезки длиной 6 и 15 см. Найти длины сторон параллелограмма, если одна из них на 7 см больше другой
1) Пусть $$BH \perp AC$$ и AH=6 , тогда HC=15/ Пусть AB=x, тогда BC=x+7
2) из $$\Delta ABH$$: $$BH^{2}=AB^{2}-AH^{2}=x^{2}-36$$
3) из $$\Delta BHC$$: $$BH^{2}+HC^{2}=BC^{2}\Leftrightarrow$$ $$x^{2}-36+225=(x+7)^{2}\Leftrightarrow$$ $$x=10=AB\Rightarrow$$ $$BC=17$$
Задание 7163
В равнобедренную трапецию вписана окружность радиуса 2 см. Найдите площадь трапеции, если длина боковой стороны равна 10 см
1) Пусть O-центр окружности, $$OH\perp BC$$ и $$OM\perp AD$$ (радиусы в точки касания )$$\Rightarrow$$ $$HK=2+2=4$$. Пусть $$CK\left | \right |HM\Rightarrow$$ $$CK=4$$
2) По свойству описанного четырехугольника : $$AB+CD=BC+AD=20$$
3) $$S_{ABCD}=\frac{BC+AD}{2}*CK=\frac{20}{2}*4=40$$
Задание 7250
Основания трапеции равны 4 см и 16 см. Найдите ее площадь, если известно, что в трапецию можно вписать и вокруг нее можно описать окружность
1) Если около нее можно описать окружность , то это равнобедренная трапеция.
2) Если в нее можно вписать окружность, то сумма боковых сторон равна сумме оснований.
3) С учетом (1) и (2): $$AB=CD=\frac{4+16}{2}=10$$
4) Пусть $$CH\perp AD\Rightarrow$$ $$HD=\frac{AD-BC}{2}=\frac{16-4}{2}=6$$
5) по т . Пифагора из $$\Delta CHD$$: $$CH=\sqrt{CD^{2}-HD^{2}}=8$$
6) $$S_{ABCD}=\frac{BC+AD}{2}*CH=10*8=80$$
Задание 8399
В окружность радиуса 3 вписана равнобедренная трапеция с углом 45 при основании и высотой, равной $$\sqrt{2}$$ . Найдите площадь этой трапеции
1) Пусть $$BH$$ и $$CM$$ высоты, тогда в $$\bigtriangleup ABH$$: $$\angle ABH=90^{\circ}-\angle=45^{\circ}$$ $$\Rightarrow$$ $$AH=HB=\sqrt{2}$$; аналогично $$CM=MD=\sqrt{2}$$
2) $$\bigtriangleup ABD$$ - вписан $$\Rightarrow$$ $$\frac{BD}{\sin A}=2\cdot2$$ $$\Rightarrow$$ $$BD=2\cdot R\sin A=2\cdot3\cdot\frac{\sqrt{2}}{2}=3\sqrt{2}$$
3) По т. Пифагора из $$\bigtriangleup BDH$$: $$HD=\sqrt{BD^{2}-BH^{2}}=4$$ $$\Rightarrow$$ $$HM=BC=4-\sqrt{2}$$
4) $$S_{ABCD}=\frac{BC+AD}{2}\cdot BH=\frac{4-\sqrt{2}+4+\sqrt{2}}{2}\cdot\sqrt{2}=4\sqrt{2}$$
Задание 10960
1)$$\ \angle A+\angle B=180{}^\circ \to \angle BAF+\angle ABF=90{}^\circ $$ (как половина суммы $$\angle A$$ и $$\angle B$$).
2) по теореме Пифагора: $$AB=\sqrt{AF^2+BF^2}=\sqrt{{24}^2+{10}^2}=25$$.
