ОГЭ
Задание 1854
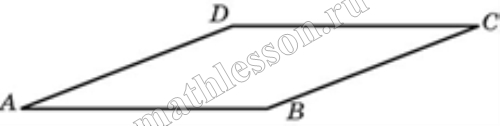
Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Перечислите эти длины в ответе через точку с запятой в порядке возрастания.
Пусть BH - высота ромба, тогда треугльник BHA - прямоугольный и $$AH=AB*\cos A=34*\frac{1}{2}=17$$, тогда HD=AD-AH=34-17=17
Задание 1855
Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
Сторона ромба равна $$\frac{36}{4}=9$$, из формулы площади ромба:$$h=\frac{S}{a}=\frac{36}{9}=4$$, где h - высота, a - сторона ромба.
Задание 1856
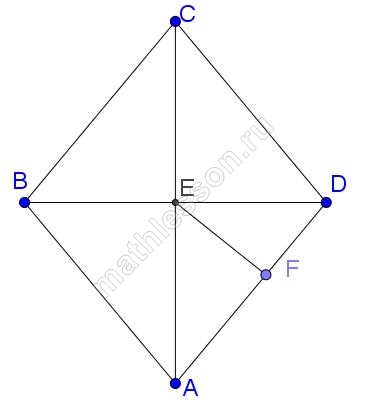
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
В ответе запишите величины различных углов в порядке возрастания через точку с запятой.
По свойству диагоналей ромба: $$AE=\frac{1}{2}AC$$, пусть AC=76, тогда AE=38. Треугольник AEF - прямоугольный, тогда $$\sin EAF=\frac{EF}{EA}=\frac{19}{38}=0,5\Rightarrow$$$$\angle EAF=30^{\circ}$$, тогда по свойству диагоналей ромба $$\angle A=60^{\circ}$$ и по свойству углов ромба $$\angle B=180-\angle A=120^{\circ}$$
Задание 1857
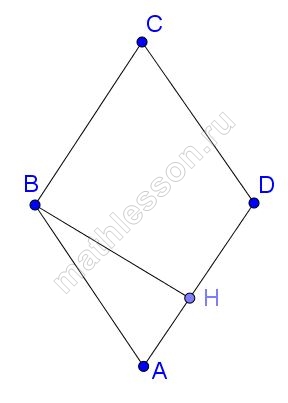
Точка O — центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR — ромб. Найдите угол ORQ. Ответ дайте в градусах.
OP=OR=PQ=QR ( по свойству ромба ), тогда, так как PR - общая, то треугольники POR И PQR равны, следовательно, $$\angle O=\angle Q$$. Пусть $$\angle Q=x$$, тогда большая дуга PR=2x (по свойству вписанного угла), тогда меньшая дуга RP=360-2x и $$\angle O=360-2x$$ ( по свойству центрального угла ), тогда $$x=360-2x\Leftrightarrow$$$$x=120$$, то есть $$\angle O=120^{\circ}$$, тогда по свойству углов ромба $$\angle P=180-\angle O=60^{\circ}$$
Задание 2968
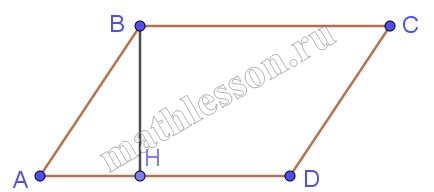
| Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? |
|
$$AB=AD$$ $$\Rightarrow$$ $$\bigtriangleup ABD$$ - равнобедренный; $$\angle B=\angle D=\frac{180-\angle A}{2}=60^{\circ}$$ $$\Rightarrow$$ $$\bigtriangleup ABD$$ - равносторонний $$\Rightarrow$$ ВН - медиана, биссектриса, высота $$\Rightarrow$$ $$AH=HD=\frac{26}{2}=13$$ |
Задание 5218
Площадь ромба равна 60, а периметр равен 30. Найдите высоту ромба.
Раз периметр равен 30, то одна сторона ромба: $$a=\frac{30}{4}=7,5$$. Высоту ромба можно найти через его площадь: $$h=\frac{S}{a}=\frac{60}{7,5}=8$$
Задание 7465
Площадь ромба равна 15, а периметр равен 20. Найдите высоту ромба.
Найдем сторону ромба: $$a=\frac{P}{4}=5$$ Найдем высоту ромба: $$h=\frac{S}{a}=3$$