ОГЭ
Задание 1823
Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
Сумма всех углов выпуклого четырехугольника составляет 360 градусов, тогда оставшийся их четырех углов равен: $$360-300=60^{\circ}$$
Задание 1825
Углы выпуклого четырехугольника относятся как 1:2:3:4. Найдите меньший угол. Ответ дайте в градусах.
Сумма углов четырехугольника составляет 360 градусов. Пусть меньший из углов (угол А) равен х, тогда остальные углы равны 2х, 3х, 4х. Тогда: $$x+2x+3x+4x=360\Leftrightarrow$$$$10x=360\Leftrightarrow$$$$x=36$$, то есть меньший угол равен 36 градусам
Задание 1826
Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Сумма противоположных углов вписанного в окружность четырехугольника составляет 180 градусов, следовательно, больший из оставшихся будет равен $$180-58=122^{\circ}$$ (второй из оставшихся $$180-82=98^{\circ}$$)
Задание 1827
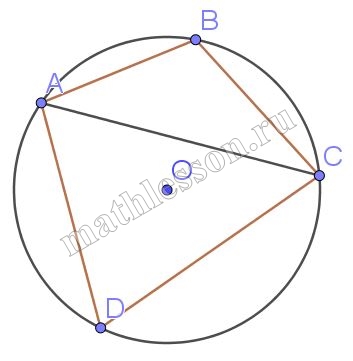
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.
Угол ABC - вписанный, следовательно, величина дуги ADC два раза больше (так как он опирается на данную дугу), тогда $$\smile ADC=272^{\circ}$$, аналогично $$\smile DC =2\angle CAD=164^{\circ}$$, тогда $$\smile AD=\smile ADC-\smile DC=272-164=108^{\circ}$$, но угол ABD опираются на эту дугу и является вписанным, следовательно, $$\angle ABD=\frac{1}{2}\smile AD=54^{\circ}$$
Задание 1828
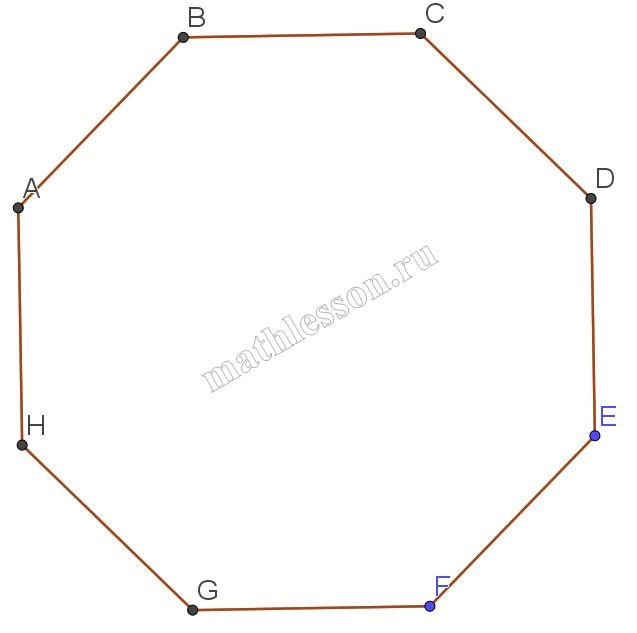
ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
Так как дан правильный восьмиугольник, то всего его углы равны. Угол же правильного n-угольника можно найти по формуле :$$\alpha =\frac{n-2}{n}*180$$, тогда $$\angle EFG=\frac{8-2}{8}*180=135^{\circ}$$
Задание 1829
Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Пусть EH - общий перпендикуляр к AB и k, тогда EH - искомое расстояние. Из треугольника AOH (прямоугольный) по теореме Пифагора: $$OH=\sqrt{OA^{2}-AH^{2}}$$, AH=0,5AB=40, тогда: $$OH=\sqrt{85^{2}-40^{2}}=75$$. EH=EO+OH=85+75=160.
Задание 1831
В выпуклом четырехугольнике ABCD AB = BC, AD = CD, ∠B = 77°, ∠D = 141°. Найдите угол A. Ответ дайте в градусах.
Так как AB = BC, AD = CD, то $$\angle A=\angle C$$. Сумма углов выпуклового четырехугольника составляет $$360^{\circ}$$, следовательно, $$\angle A=\frac{360^{\circ}-\angle B -\angle D}{2}=\frac{360-77-141}{2}=71^{\circ}$$
Задание 1832
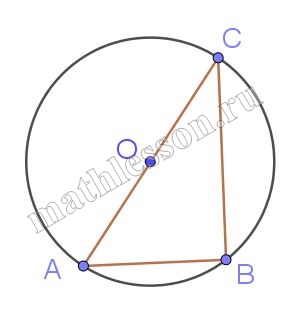
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите $$\angle C$$, если $$\angle A=81^{\circ}$$. Ответ дайте в градусах.
Так ка сторона проходит через центр окружности, то треугольник является прямоугольным, следовательно: $$\angle C=90^{\circ}-\angle A=90^{\circ}-81^{\circ}=9^{\circ}$$
Задание 11038
Диагональ прямоугольника образует угол $$63^{\circ}$$ с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
