ОГЭ
Задание 3843
Постройте график функции $$y=1-\frac{2x+4}{x^{2}+2x}$$ и определите, при каких значениях а прямая $$y=а$$ не имеет с графиком ни одной общей точки.
$$y=1-\frac{2x+4}{x^{2}+2x}=1-\frac{2(x+2)}{x(x+2)}=1-\frac{2}{x}$$
$$x\neq0$$; $$x\neq2$$ $$\Rightarrow$$ $$(-2;2)$$ не входит
Тогда $$y=2$$; $$y=1$$ не имеют общих точек с $$y=1-\frac{2x+4}{x^{2}+2x}$$
Задание 4534
Постройте график функции $$y=2+\frac{x+2}{x^{2}+2x}$$ и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.
$$y=2+\frac{x+2}{x^{2}+2x}=2+\frac{x+2}{x(x+2)}=2+\frac{1}{x}$$; $$x^{2}\neq2x\neq0$$; $$x\neq0$$; $$x\neq-2$$.
$$m=1,5$$; $$m=2$$
Задание 5271
Постройте график функции $$y=-1-\frac{x-2}{x^{2}-4}$$ и определите, при каких значениях $$a$$ прямая $$y=a$$ не имеет с графиком ни одной общей точки.
ОДЗ: $$x^{2}-4 \neq 0 \Leftrightarrow$$$$x\neq\pm 2$$. Преобразуем правую часть функции: $$-1-\frac{x-2}{x^{2}-4}=$$$$-1-\frac{x-2}{(x-2)(x+2)}=$$$$-1-\frac{1}{x+2}$$
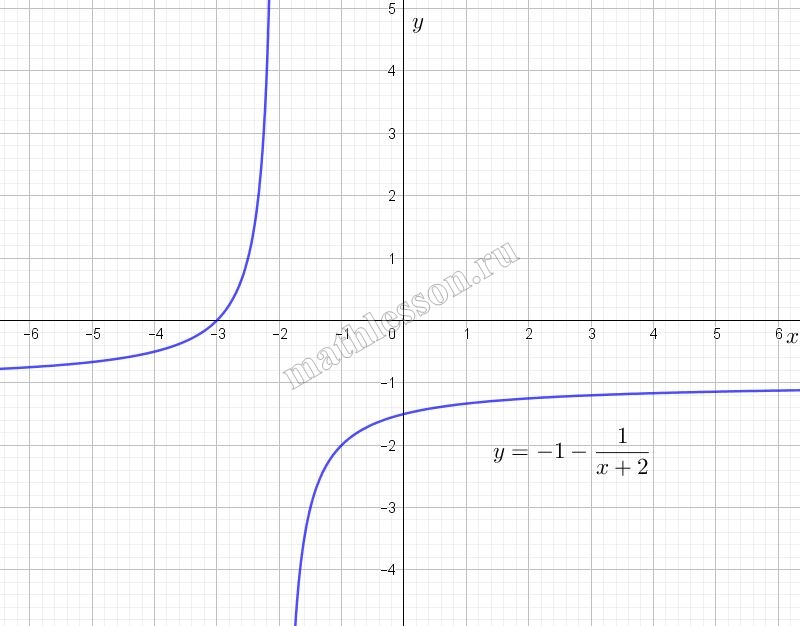
То есть график функции $$y_{1}=-1-\frac{1}{x+2}$$ и график искомой функции совпадают, если к $$y_{1}$$ применить ОДЗ для искомой. График функции $$y_{1}$$ - гипербола, смещенная на 1 единицу вних и на две влево относительно графика эталонной обратной пропорциональности $$y=\frac{1}{x}$$. Начертим график функции $$y_{1}$$:
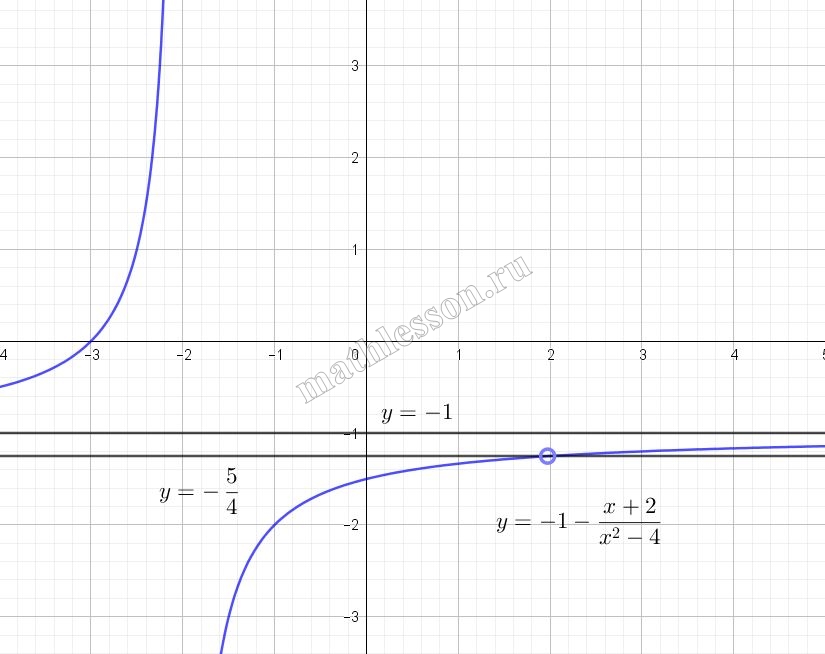
Учтем, что $$x\neq\pm 2$$. В случае $$x\neq -2$$ можно отдельно не рассматривать, так как это условие уже выполняется для графика функции $$y_{1}$$. Для $$x\neq 2$$: подставим значение $$x=2$$ в функции $$y_{1}$$: $$y_{1}(2)=-1-\frac{1}{2+2}=-\frac{5}{4}$$. То есть точку, с координатами $$(2;-\frac{5}{4})$$ необходимо отметить пустой на графике функции $$y_{1}$$ и тогда мы получим график искомой функции:
Прямая $$y=a$$ - прямая паралленая оси Ох, чтобы она не имела с графиком искомой функции точек пересечения она должны использоваться следующие значения $$a=-1;-\frac{5}{4}$$:
Задание 6070
Постройте график функции $$y=\frac{x^{2}-25}{x^{2}-5x}$$ и определите, при каких значениях a прямая $$y=a$$ не имеет с графиком ни одной общей точки.
$$y=\frac{x^{2}-25}{x^{2}-5x}$$
ОДЗ: $$x^{2}-5x\neq 0 \Leftrightarrow x(x-5)=0\Leftrightarrow$$$$ x\neq 0; x\neq 5\Rightarrow x\in (-\infty; 0)\cup(5 ;+\infty ).$$
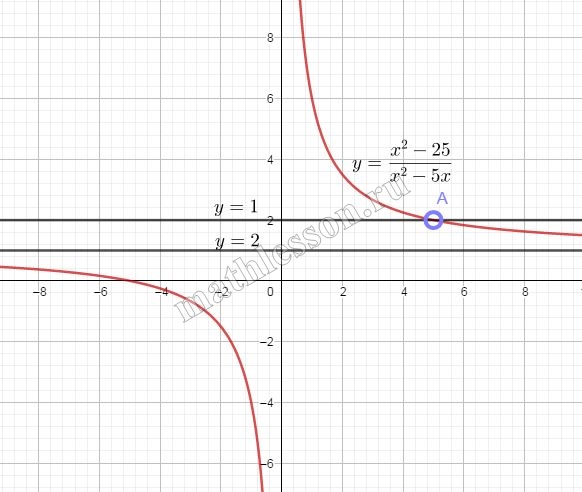
Упростим выражение: $$\frac{x^{2}-25}{x^{2}-5x}=\frac{(x-5)*(x+5)}{x(x-5)}=\frac{x+5}{x}=1+\frac{5}{x}$$ Т.е. график $$y=1+\frac{5}{x}$$ такой же, как $$y=\frac{x^{2}-25}{x^{2}-5x}$$ при условии ОДЗ:
Прямая $$y=a$$ - это прямая, параллельная оси Ох. Она не будет иметь пересечения с графиком исходной функции при a=2 и a=1.
Задание 6449
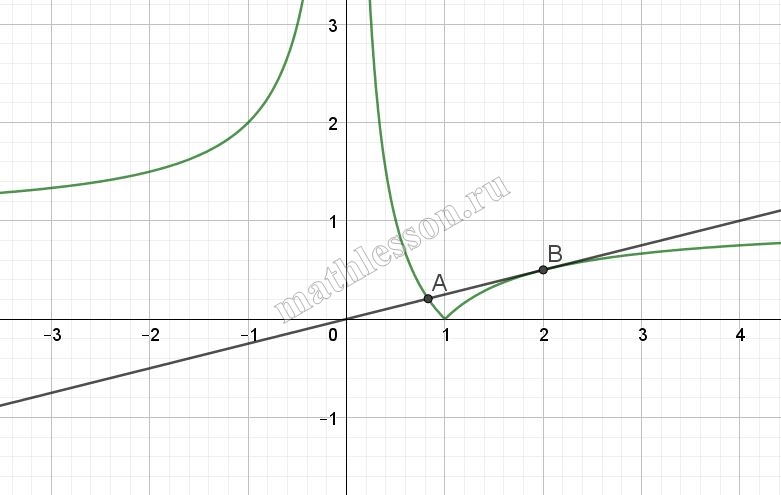
Постройте график функции $$y=|\frac{x-1}{x}|$$ и определите, при каких значениях а прямая y=ах имеет с графиком ровно две общие точки.
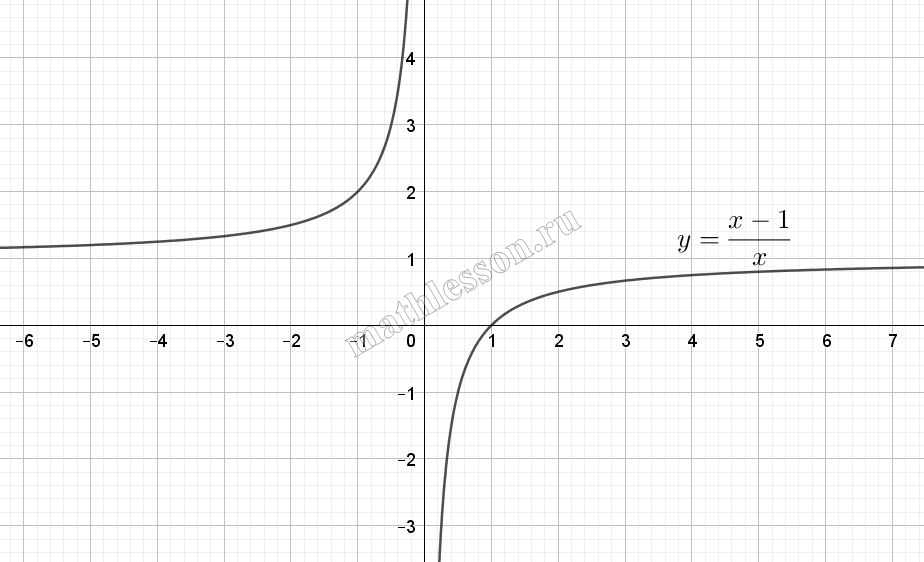
Преобразуем правую часть функции: $$y=\left | \frac{x-1}{x} \right |=\left | 1-\frac{1}{x} \right |$$. То есть у нас дан график функции $$y=\frac{1}{x}$$, смещенный на 1 вверх по оси Оу и отображенный относительно оси Оу.
Кроме того, наличие модуля отобрадает ту часть графика, которая находится под осью Ох (показана на рисунке), симметрично относительно Ох:
Итоговый график функции будет выглядить, как:
Необходимо найти такое значение а, при котором будет ровно два решения. В таком случае график прямой должен касаться графика исходной функции (точка B):
Так как касается в той части графика, где функции (с учетом раскрытия модуля) выглядит как $$y=1-\frac{1}{x}$$. Так как там касается, то должна быть одна точка пересечения с данным графиком: $$ax=1-\frac{1}{x}\Leftrightarrow$$$$\frac{ax^{2}-x+1}{x}=0$$ При этом $$D=1-4a=0\Leftrightarrow$$$$a=\frac{1}{4}=0,25$$
Задание 6740
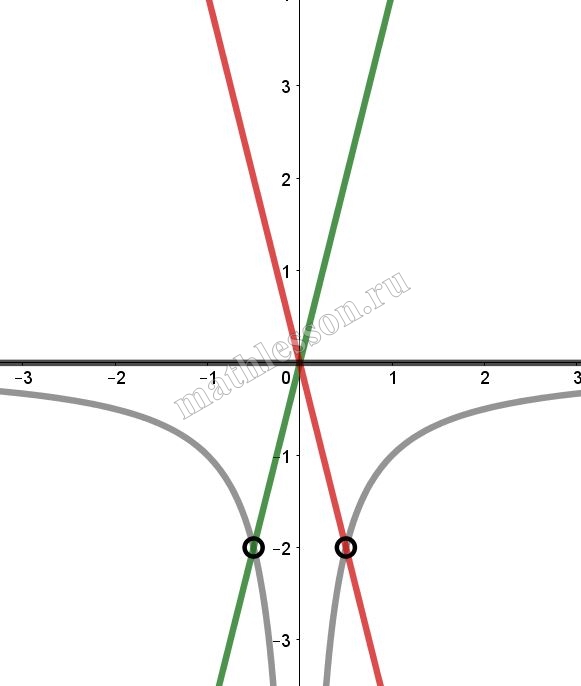
Постройте график функции $$y=\frac{2|x|-1}{|x|-2x^{2}}$$ и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.
ОДЗ: $$\left | x \right |-2x^{2}\neq 0\Leftrightarrow$$ $$\left | x \right |-2\left | x \right |^{2} \neq 0\Leftrightarrow$$ $$\left | x \right |(1-2\left | x \right |)\neq 0\Leftrightarrow$$ $$\left\{\begin{matrix}x\neq 0\\ x\neq 0,5\\ x\neq -0,5\end{matrix}\right.$$.
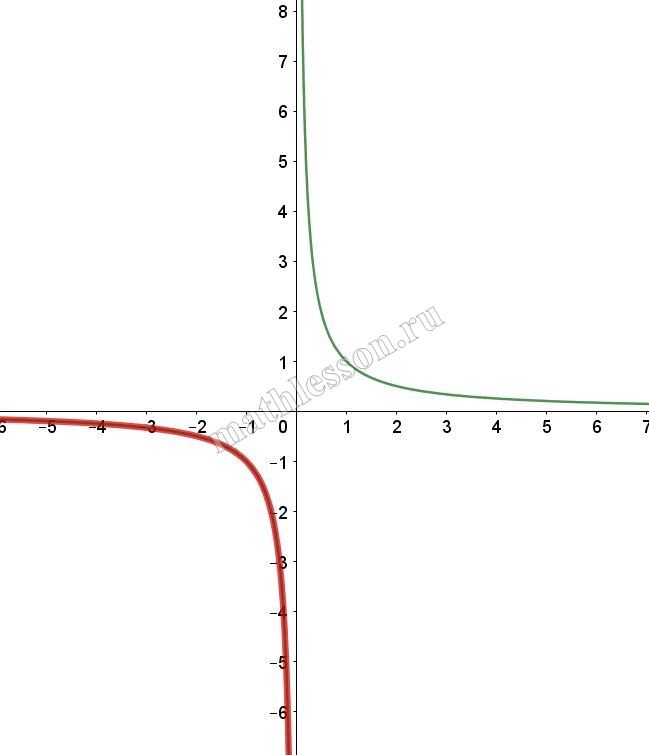
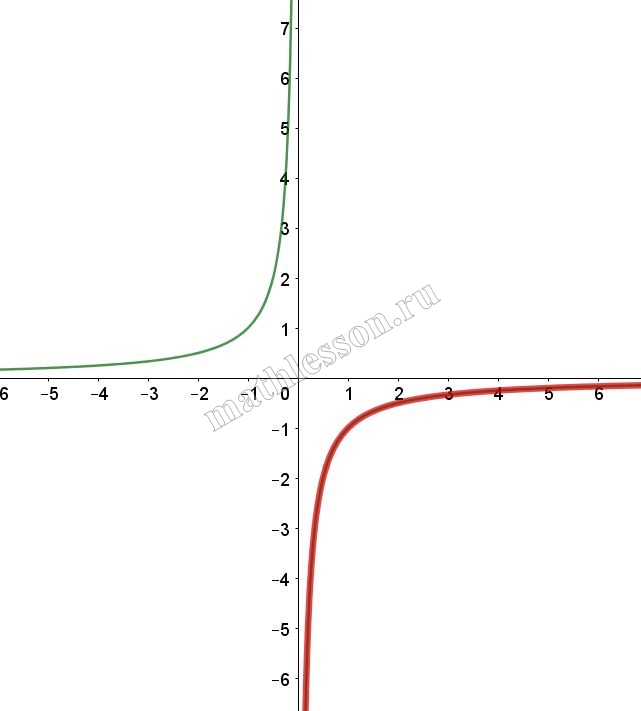
При $$x>0$$: $$y=\frac{2x-1}{x(1-2x)}=-\frac{1}{x}$$ (выдерена красным)
При $$x<0$$: $$y=\frac{-2x-1}{-x-2x^{2}}=\frac{1}{x}$$(выделена красным)
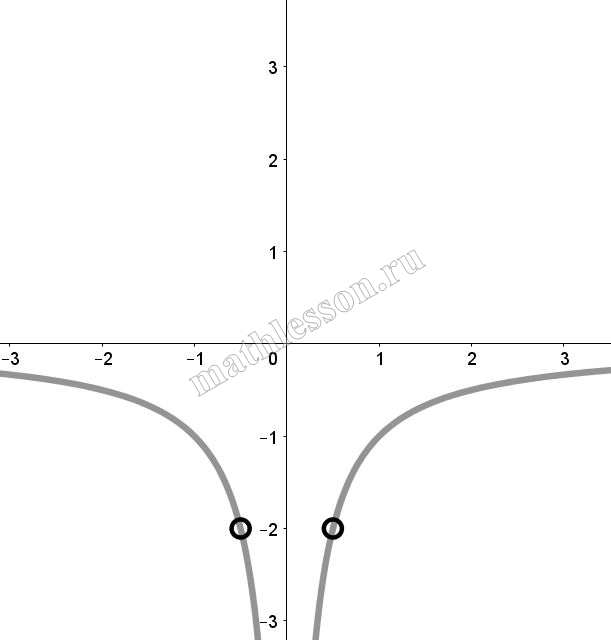
Итоговый график с учетом ОДЗ:
Найдем k: $$y=kx$$ проходит через (-0,5 ; -2): $$-2=-0,5*k\Rightarrow k=4$$(зеленая) и через (0,5; -2): $$-2=0,5k\Rightarrow k=-4$$(красная). При k=0 (черная) тоже не имеет пересечений
Задание 6787
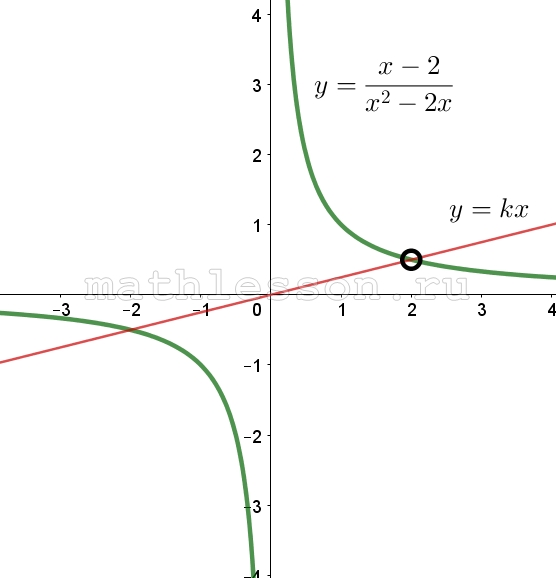
Постройте график функции $$y=\frac{x-2}{x^{2}-2x}$$ и определите, при каких значениях k прямая $$y=kx$$ имеет с графиком ровно одну общую точку.
Найдем ограничения по x: $$x^{2}-2x\neq 0\Leftrightarrow$$ $$x\neq 0 x\neq 2(1)$$. Тогда $$y=\frac{x-2}{x(x-2)}=\frac{1}{x}$$ с учетом (1) аналогичен искомой функции
Построим график функции:
$$y=kx$$ имеет 1 общую точку если проходит через (2;0,5): $$0,5=2k\Rightarrow$$ $$k=\frac{1}{4}$$
Задание 6906
Постройте график функции $$y=1+\frac{x-3}{x^{2}-3x}$$ и определите, при каких значениях а прямая y=а не имеет с графиком ни одной общей точки.
$$y=1+\frac{x-3}{x^{2}-3x}$$$$\Leftrightarrow$$ $$y=1+\frac{x-3}{x(x-3)}$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}y=1+\frac{1}{x}\\x-3\neq 0\end{matrix}\right.$$
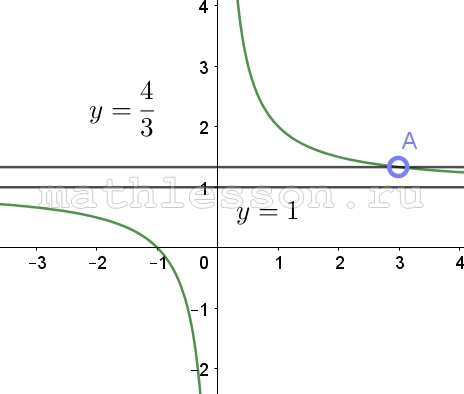
Начертим график данной функции:
Найдем оординату точки А: $$y(3)=1+\frac{1}{3}=\frac{4}{3}$$
Т.к. $$y=a$$ – прямая, параллельная Ox, то не будет иметь общих точек при $$a=\frac{4}{3}$$ (проходит через А) и $$a=1$$ (проходит через горизонтальную асимптоту)
Задание 7135
Постройте график функции $$y=-1-\frac{x-1}{x^{2}-x}$$ и определите, при каких значениях а прямая y=а не имеет с графиком ни одной общей точки
Упростим формулу: $$y_{1}=-1-\frac{x-1}{x(x-1)}=-1-\frac{1}{x}$$ . Следовательно , график функции $$y_{1}$$ совпадает с $$y$$ при учете , что $$x\neq 1$$.
Не имеет при $$a=-2$$ и при $$a=-1$$.